RBA Annual Conference – 2009 Discussion
1. Anthony Richards
In these comments I will begin with a discussion of how central banks typically use measures of core or underlying inflation[1], and then discuss the specific methodology that Francesco Ravazzolo and Shaun Vahey propose.[2]
How do central banks use measures of underlying inflation?
There is significant ‘noise’ in headline inflation. Good measures of underlying inflation are ones that help to abstract from this noise and give a better read of the ‘signal’. Understanding the current pace of inflation is important for central banks as a starting point for forecasts. In Brischetto and Richards (2006), we argue that good measures of underlying inflation are likely to have some short-term predictive power for inflation. I would stress that this is not about the predictability of inflation in two or three years: central banks use their economic models to forecast inflation at that horizon. Rather, tests of near-term predictability provide an indication of which measures of inflation have less noise and relatively more signal.
At the RBA, we look at a wide range of measures of inflation in addition to headline inflation. These include the following:
- A number of ‘exclusion measures’, such as those that exclude automotive fuel and fruit & vegetables, as well as items that may be significantly affected by policy (for example, deposit & loan facilities, the prices of which have been affected both by measurement issues and by the large movements in the cash rate over the past year).
- A number of trimmed-mean and weighted-median measures calculated using both quarterly and annual price changes. In addition to the standard measures calculated by the ABS, we also calculate measures using price data disaggregated by both expenditure item and capital city, reflecting the innovation proposed for the United States in Brischetto and Richards (2006).
- Given that there is strong evidence of seasonality in some individual CPI components and some evidence of seasonality in the overall CPI, we calculate a seasonally adjusted CPI, as well as seasonally adjusted exclusion measures.
- Finally, we also look at some more technical methods, such as factor and time-series models.
Based on this, we reach a judgment about the trend in inflation over the past quarter or year, attempting to abstract from noise from individual items, and thinking about the particular factors influencing the data. As part of this process, we often do some (mental) time-series filtering or smoothing.
We then prepare forecasts of inflation, both underlying and headline, based on a suite of models, with the current pace of underlying inflation an important input into these forecasts. We recognise that any forecast has a distribution, and spend a fair bit of time thinking about how the world could be different (although, relative to Francesco and Shaun, we spend relatively more time thinking about the central forecast than thinking about the width of the distribution).
This paper
Francesco and Shaun start with the premise, consistent with the comments above, that measures of core inflation should be informative about inflation probabilities.
In simple terms, their methodology is as follows. They begin with quarterly inflation in CPI components (either 10 expenditure classes or 8 capital cities) up to time t. They then fit autoregressive models with four lags (AR(4)) explaining each component, and take the fitted values and densities for each component in period t+1. Then they mean-adjust (or re-centre) each fitted value and density to match mean CPI inflation. The re-centred AR(4) predictions and densities are then combined. This combined forecast is called ‘core inflation’ in period t+1, with an accompanying density. For some of these steps, the authors use some fairly advanced techniques to which my brief description does not do justice. Of course, this highly technical approach will be a two-edged sword and might hinder any attempt to use the proposed measure in a central bank's communication with the public.
Although the paper is titled ‘Measuring Core Inflation in Australia with Disaggregate Ensembles’, it is more about modelling and forecasting than about measuring in the conventional sense: indeed the authors can give us period t+1 underlying inflation before the statistical office has published even the headline inflation data for that period.[3]
Nevertheless, it is worth asking how it relates to existing measures of underlying inflation. Most measures of underlying inflation can be viewed as providing some degree of noise reduction through either time-series smoothing or through cross-sectional reweighting. This paper can be thought of as having elements of both time-series smoothing (the AR(4) modelling to generate forecasts) and reweighting (the combination of different forecasts).
Regarding the reweighting, it is worth comparing how the weights in this proposed measure compare with the conventional CPI and with a measure like the RBA's 15 per cent trimmed mean. Table 3 in their paper indicates that the city-based ensemble significantly down-weights Sydney and Melbourne, and significantly up-weights Darwin, Canberra and Hobart. Similarly, one can compare the weights on the expenditure groups with the CPI weights: their Table 2 shows that the expenditure-weighted ensemble significantly down-weights housing, and up-weights education relative to the CPI. In addition, one might consider how the weights in the proposed methodology compare with weights in trimmed-mean measures. This is not, of course, straightforward because the weights in the trimmed mean are highly time-varying. However, we might get an approximation from the average frequency with which CPI items are inside the central 70 per cent of the price-change distribution, over time. Such a calculation shows that the departures from CPI weights are much larger for the proposed methodology than for the trimmed mean.
Such large deviations from CPI weights are risky in the computation of measures of underlying inflation, because over long periods of time there may be persistent differences in the average inflation rates of different types of items in the CPI. If so, a significant reweighting of CPI components may yield a measure that is biased relative to the CPI, which is an undesirable feature of a measure of underlying inflation. Of course, it is possible that Francesco and Shaun's step of re-centring the mean growth rates reduces this risk.
Regarding the time-series smoothing, it is possible that the AR(4) modelling gives more smoothing than is appropriate. And the use of raw, rather than seasonally adjusted, data might exacerbate this given that price increases for some expenditure groups are highly seasonal. For example, there are four of the ten expenditure groups for which seasonally unadjusted data suggest that AR(4) models are appropriate, whereas seasonally adjusted data suggest that AR(1) or AR(2) models are appropriate. Hence it seems that the AR(4) modelling using seasonally unadjusted data places excessive weight on quite lagged data and insufficient weight on the more recent data.
Regarding the results, Francesco and Shaun's methodology provides a distribution of core inflation, but I will focus on the centre of the distribution.[4] A first point to note is that the central estimate for core inflation does not show all that much medium-term variation.[5] The authors suggest that the RBA trimmed-mean and weighted-median measures may have overstated core inflation in 2008. But an alternative reading of their results would be that their estimates might not show enough movement to be good estimates of underlying inflation.
As noted above, the central estimate for ‘core inflation’ is the central forecast for next period's CPI inflation. So one might ask how good their central forecasts are. As a benchmark for their forecast evaluations, Francesco and Shaun use an AR(4) model for headline inflation, and they find that their point forecasts ‘are competitive with the AR(4) benchmark’ (p 188). But it turns out that an AR(4) model of headline CPI inflation has an adjusted R-squared, in-sample, of essentially zero. So when the authors say their model is competitive with an AR(4), we should not take that as a particularly high hurdle.
A natural question, assuming one is using this approach, is whether one can come up with simple one-step-ahead forecasts of headline inflation that do better than either the AR(4) model or Francesco and Shaun's disaggregate ensembles. One obvious candidate in my mind was lagged trimmed-mean inflation. Indeed, when one adds lagged trimmed-mean inflation to an AR(4) model (or to my own simple attempted replication of Francesco and Shaun's methodology) it is clearly significant, although the adjusted R-squared is less than 0.10. So if one is trying to forecast the next period's headline inflation, one can indeed do better than an AR(4) model or the core measures proposed in this paper.
So does this mean that short-term inflation is close to unpredictable? Actually, it is somewhat predictable, you just have to be predicting something which has less noise than headline inflation. Again, one might consider trimmed-mean inflation. For example, I have used data for Australia, the euro area, Japan and the United States to run a regression explaining quarterly or three-month-ended trimmed-mean inflation by (non-overlapping) lagged headline and lagged trimmed-mean inflation. For all four economies, there is a reasonably high adjusted R-squared, with lagged trimmed-mean inflation highly significant, but lagged CPI inflation either insignificant or the ‘wrong’ sign.
These results stem from the fact that trimmed-mean inflation, unlike CPI inflation, is relatively smooth. As we can see in Figure 1, trimmed-mean inflation appears to abstract from much of the noise in CPI inflation, raising the possibility that we may actually be able to see some signal in monthly or quarterly inflation data.
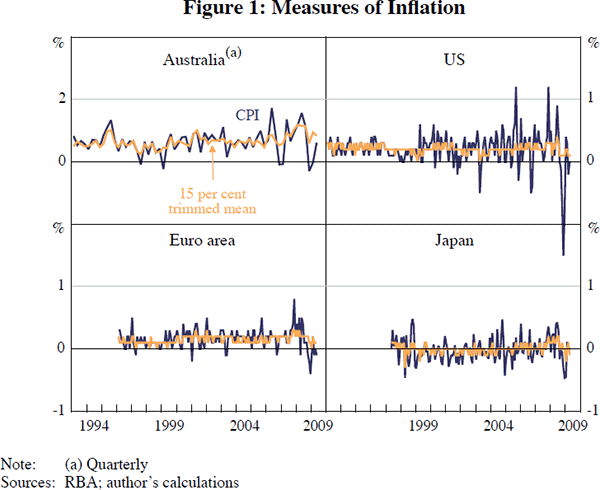
None of this is to suggest that the RBA or other central banks should necessarily be targeting trimmed-mean inflation or any other underlying measure. In Australia, the target is CPI inflation, but we have found that underlying measures can help us understand the trend in inflation, which should help us meet our broader goals for monetary policy.
Summary and suggestions
Overall, I agree with the premise of the paper that measures of underlying inflation should be judged in part on what information they provide about near-term inflation outcomes. While the paper's analysis of density functions is new, I suspect most readers will be more interested in its point estimates of underlying inflation. Here, my sense is that the suggested methodology, as currently implemented, has not yet made a strong case that it is an improvement over traditional underlying measures (including trimmed means) that use the cross-section of the data to remove some of the noise in headline inflation.
If the authors expand on their work, I would suggest that they should consider focusing on three aspects. First, it is important to deal with seasonality, especially when dealing with component-level data. Second, they should consider the possibility of adding other predictors to the ensembles, the obvious one being trimmed-mean inflation, but there are no doubt others. Finally, I think they should take more seriously the idea that the headline CPI is very noisy in the short term. If they find they really cannot predict quarter-on-quarter movements in the CPI, then their one-step-ahead prediction will always look like something close to a straight line and may not be informative about swings in underlying inflation. So they should also look at the short-term predictability of other inflation measures.
Footnotes
The terms core and underlying inflation are often used fairly interchangeably. However, many use the term ‘core’ to refer to a specific exclusion measure of underlying inflation (typically the CPI excluding automotive fuel and some food items). I will use the term ‘underlying’ to refer to a general concept, rather than any specific measure. [1]
Many of the ideas in these comments are borrowed from Brischetto and Richards (2006). [2]
This seems odd: the authors should consider changing their date/naming convention: although the forecast may be for inflation in period t+1, it uses period t data and might be better called underlying inflation for period t. [3]
I leave open the broader question of whether it would be desirable for a published measure of core inflation to have a wide confidence interval around it. However, I think one could make a good case that central banks should always give the sense that the future is uncertain and sometimes even that the current data are uncertain, but they should not overdo this. [4]
And, much of the short-term variation in the measure appears to be seasonal. This highlights the need to deal with seasonality anytime one is working with disaggregated CPI data. Another data issue to be dealt with when working with Australian data is the one-off price jump due to the tax changes of 1999–2000. [5]
Reference
Brischetto A and A Richards (2006), ‘The Performance of Trimmed Mean Measures of Underlying Inflation’, RBA Research Discussion Paper No 2006-10.
2. General Discussion
Francesco Ravazzolo and Shaun Vahey's paper generated debate on the possible uses of core inflation measures, including: as modelling tools; for internal bank discussion; or to communicate inflation outcomes to the public. One participant noted that an argument against using core inflation as a device for communication is that it requires convincing explanations about what is being excluded. For instance, it is difficult to justify excluding energy prices from a measure of inflation when expenditure on energy is often foremost in consumers' minds. Some other participants were of the same opinion, questioning the value of core inflation measures and suggesting that they are best suited to internal deliberations. Someone thought that it would be helpful for inflation measures to differentiate between those prices that are relatively flexible and those that are ‘sticky’, with the latter of greater concern to policy-makers. Shaun Vahey replied by suggesting that the measure of core inflation constructed in the paper was useful both for internal discussions and communication with the public. On the latter, he emphasised the ability of the approach presented in the paper to offer probabilistic forecasts of core inflation, which he argued are reasonably easy to understand.
The rest of the discussion considered modelling choices made by the authors. A participant suggested that the model should use more disaggregated CPI components, and avoid using the city disaggregated components. In response, Shaun Vahey noted that the ensemble methodology proposed has the capacity to handle any form of disaggregation. He cited the example of weather forecasting, from which the ensemble methodology was derived, which uses up to 50 components of disaggregation. He indicated that including the city components helps improve the model's predictive performance, so he was satisfied with this choice.
The one-period forecasting horizon considered in the paper was queried, with the suggestion that longer horizons should be considered. However, if the latter approach was taken, some people thought that a more appropriate predictive model, which also incorporates the responses of interest rates and output, should be considered. Shaun Vahey agreed with the sentiments expressed, and suggested that they justified the paper's focus on one-quarter-ahead forecasts.
One participant suggested that the model presented in the paper would not pick up any second-round effects following, say, a relative price shock because the autoregressive model with four lags imposed too much persistence on the inflation process. Shaun Vahey reiterated that a key feature of the model is its use of time-varying weights on the components, which gives the model the ability to adapt relatively quickly to shocks.