RBA Annual Conference – 2009 Determinants of Agricultural and Mineral Commodity Prices Jeffrey A Frankel and Andrew K Rose[1]
Abstract
Prices of most agricultural and mineral commodities rose strongly in the past decade, peaking sharply in 2008. Popular explanations included strong global growth (especially from China and India), easy monetary policy (as reflected in low real interest rates or expected inflation), a speculative bubble (resulting from bandwagon expectations) and risk (possibly resulting from geopolitical uncertainties). Motivated in part by this episode, this paper presents a theory that allows a role for macroeconomic determinants of real commodity prices, along the lines of the ‘overshooting’ model: the resulting model includes global GDP and the real interest rate as macroeconomic factors. Our model also includes microeconomic determinants: inventory levels, measures of uncertainty, and the spot-futures spread. We estimate the equation in a variety of different ways, for 11 individual commodities. Although two macroeconomic fundamentals – global output and inflation – both have positive effects on real commodity prices, the fundamentals that seem to have the most consistent and strongest effects are microeconomic variables: inventories, volatility and the spot-futures spread. There is also evidence of a bandwagon effect.
1. Macroeconomic Motivation
Questions related to the determination of prices for oil and other mineral and agricultural commodities have always fallen predominantly in the province of microeconomics. Nevertheless, there are times when so many commodity prices are moving so far in the same direction that it becomes difficult to ignore the influence of macroeconomic phenomena. The decade of the 1970s was one such time; recent history provides another. A rise in the price of oil might be explained by ‘peak oil’ fears, a risk premium related to instability in the Persian Gulf, or political developments in Russia, Nigeria or Venezuela. Spikes in certain agricultural prices might be explained by drought in Australia, shortages in China, or ethanol subsidies in the United States. But it cannot be a coincidence that almost all commodity prices rose together during much of the past decade, and peaked so abruptly and jointly in mid 2008. Indeed, from 2003–2008, three theories (at least) competed to explain the widespread ascent of commodity prices.
First, and perhaps most standard, was the global demand growth explanation. This argument stems from the unusually widespread growth in economic activity – particularly including the arrival of China, India and other entrants to the list of important economies, together with the prospects of continued high growth in those countries in the future. This growth has raised the demand for, and hence the price of, commodities. While reasonable, the size of this effect is uncertain.
The second explanation, also highly popular, at least outside of academia, was destabilising speculation. Many commodities are highly storable; a large number are actively traded on futures markets. We can define speculation as the purchases of the commodities – whether in physical form or via contracts traded on an exchange – in anticipation of financial gain at the time of resale. There is no question that speculation, so defined, is a major force in the market. However, the second explanation is more specific: that speculation was a major force that pushed commodity prices up during 2003–2008. In the absence of a fundamental reason to expect higher prices, this would be an instance of destabilising speculation or of a speculative bubble. But the role of speculators need not be pernicious; perhaps speculation was stabilising during this period. If speculators were short on average (in anticipation of a future reversion to more normal levels), they would have kept prices lower than they otherwise would have been.
Much evidence has been brought to bear on this argument. To check if speculators contributed to the price rises, one can examine whether futures prices lay above or below spot prices, and whether their net open positions were positive or negative.[2] A particularly convincing point against the destabilising speculation hypothesis is that commodities without any futures markets have experienced approximately as much volatility as commodities with active derivative markets. We also note that efforts to ban speculative futures markets have usually failed to reduce volatility in the past. Another relevant issue is the behaviour of inventories, which seems to undermine further the hypothesis that speculators contributed to the 2003–2008 run-up in prices. The premise is that inventories were not historically high, and in some cases were historically low. Thus speculators could not plausibly have been betting on price increases and could not, therefore, have added to the current demand.[3] One can also ask whether speculators seem to exhibit destabilising ‘bandwagon expectations’. That is, do speculators seem to act on the basis of forecasts of future commodity prices that extrapolate recent trends? The case for destabilising speculative effects on commodity prices remains an open one.
The third explanation, somewhat less prominent than the first two, is that easy monetary policy was at least one of the factors contributing to either the high demand for, or low supply of, commodities. Easy monetary policy is often mediated through low real interest rates.[4] Some have argued that high prices for oil and other commodities in the 1970s were not exogenous, but rather a result of easy monetary policy.[5] Conversely, a substantial increase in real interest rates drove commodity prices down in the early 1980s, especially in the United States. High real interest rates raise the cost of holding inventories; lower demand for inventories then contributes to lower total demand for oil and other commodities. A second effect of higher interest rates is that they undermine the incentive for oil-producing countries to keep crude under the ground. By pumping oil instead of preserving it, OPEC countries could invest the proceeds at interest rates that were higher than the return from leaving it in the ground. Higher rates of pumping increase supply; both lower demand and higher supply contribute to a fall in oil prices. After 2000, the process went into reverse. The Federal Reserve cut real interest rates sharply in 2001–2004, and again in 2008. Each time, it lowered the cost of holding inventories, thereby contributing to an increase in demand and a decline in supply.
Critics of the interest rate theory as an explanation of the boom that peaked in 2008 point out that it implies that inventory levels should have been high, but argue that they were not. This is the same point that has been raised in objection to the destabilising speculation theory. For that matter, it can be applied to most theories. Explanation number one, the global boom theory, is often phrased in terms of expectations of China's future growth path, not just its currently high level of income; but this factor too, if operating in the market place, should in theory work to raise demand for inventories.[6]
How might high demand for commodities be reconciled with low observed inventories? One possibility is that researchers are looking at the wrong inventory data. Standard data inevitably exclude various components of inventories, such as those held by users or those in developing countries. They typically exclude deposits in the ground, uncut forests and crops and livestock in the fields. In other words, what is measured in inventory data is small compared to reserves. The decision by producers to pump oil today or to leave it underground for the future is more important than the decisions of oil companies or downstream users to hold higher or lower inventories. And the lower real interest rates of 2001–2005 and 2008 clearly reduced the incentive for oil producers to pump oil, relative to what it would otherwise have been.[7] We classify low extraction rates as low supply and high inventories as high demand; but either way the result is upward pressure on prices.
In 2008, enthusiasm for explanations number two and three, the speculation and interest rate theories, increased, at the expense of explanation number one, the global boom. Previously, rising demand from the global expansion, especially the boom in China, had seemed the obvious explanation for rising commodity prices. But the sub-prime mortgage crisis hit the United States around August 2007. Virtually every month thereafter, forecasts of growth were downgraded, not just for the United States but for the rest of the world as well, including China.[8] Meanwhile commodity prices, far from declining as one might expect from the global demand hypothesis, climbed at an accelerated rate. For the year following August 2007, at least, the global boom theory was clearly irrelevant. That left explanations number two and three.
In both cases – increased demand arising from either low interest rates or expectations of capital gains – detractors pointed out that the explanations implied that inventory holdings should be high and continued to argue that this was not the case.[9] To repeat a counter-argument, especially in the case of oil, what is measured in inventory data is small compared to reserves under the ground.
This paper presents a theoretical model of the determination of prices for storable commodities that gives full expression to such macroeconomic factors as economic activity and real interest rates. However, we do not ignore other fundamentals relevant for commodity price determination. To the contrary, our model includes a number of microeconomic factors including (but not limited to) inventories. We then estimate the equation using both macroeconomic and commodity-specific microeconomic determinants of commodity prices. To preview the results, most of the hypothesised determinants of real commodity prices receive support, when the data are aggregated across commodities: inventories, uncertainty, speculation, economic growth and expected inflation. The main disappointment is that the real interest rate does not appear to have a significant effect.
2. A Theory of Commodity Price Determination
Most agricultural and mineral products differ from other goods and services in that they are both storable and relatively homogeneous. As a result, they are hybrids of assets – where price is determined by supply of and demand for stocks – and goods, for which the flows of supply and demand matter.[10]
The elements of an appropriate model have long been known.[11] The monetary aspect of the theory can be reduced to its simplest algebraic essence as a relationship between the real interest rate and the spot price of a commodity relative to its expected long-run equilibrium price. This relationship can be derived from two simple assumptions. The first governs expectations. Let:
s ≡ the natural logarithm of the spot price,
p ≡ the (log of the) economy-wide price index,
q ≡ s–p, the (log) real price of the commodity, and
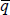 ≡ the long-run (log) equilibrium real price of the commodity.
≡ the long-run (log) equilibrium real price of the commodity.
Market participants who observe the real price of the commodity today lying either above or below its perceived long-run value expect it to regress back to equilibrium in the future over time, at an annual rate that is proportionate to the gap:
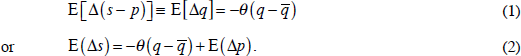
Following the classic Dornbusch (1976) overshooting paper, which developed the model for the case of exchange rates, we begin by simply asserting the reasonableness of the form of expectations in these equations. It seems reasonable to expect a tendency for prices to regress back toward long-run equilibrium. But, as in that paper, it can be shown that regressive expectations are also rational expectations, under certain assumptions regarding the stickiness of prices of other goods (manufactures and services) and a certain restriction on the parameter value θ (Frankel 1986).
One alternative that we consider below is that expectations also have an extrapolative component to them. We model this as:
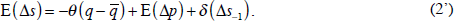
The next equation concerns the decision whether to hold the commodity for another period – leaving it in the ground, on the trees, or in inventory – or to sell it at today's price and use the proceeds to earn interest, an equation familiar from Hotelling's celebrated logic. The expected rate of return to these two alternatives must be the same:
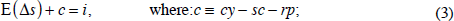
cy ≡ convenience yield from holding the stock (for example, the insurance value of having an assured supply of some critical input in the event of a disruption, or in the case of a commodity like gold, the psychic pleasure of holding it);
sc ≡ storage costs (for example, feed lot rates for cattle, silo rents and spoilage rates for grains, rental rates on oil tanks or oil tankers, costs of security to prevent plundering by others, etc);[12]
rp ≡ E(Δs) – (f−s) ≡ risk premium, where f is the log of the forward/futures rate at the same maturity as the interest rate. The risk premium is positive if being long in commodities is risky; and
i ≡ the nominal interest rate.[13]
There is no reason why the convenience yield, storage costs or the risk premium should be constant over time. If one is interested in the derivatives markets, one often focuses on the forward discount or slope of the futures curve, f−s in log terms (also sometimes called the ‘spread’ or the ‘roll’). For example, the null hypothesis that the forward spread is an unbiased forecast of the future change in the spot price has been tested extensively.[14] This issue does not affect the questions addressed in this paper, however. Here we note only that one need not interpret the finding of bias in the futures rate as a rejection of rational expectations; it could be due to a risk premium. From Equation (3), the spread is given by:
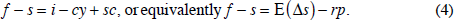
On average, f−s tends to be negative. This phenomenon, ‘normal backwardation’, suggests that convenience yield on average outweighs the interest rate and storage costs.[15] To get our main result, we simply combine Equations (2) and (3):
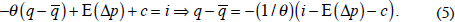
Equation (5) says that the real price of the commodity, measured relative to its long-run equilibrium, is inversely proportional to the real interest rate (measured relative to the term c, which could be described as the net convenience yield – that is, the convenience yield after accounting for storage costs and any risk premium). When the real interest rate is high, as in the 1980s, money will flow out of commodities. This will continue until the prices of commodities are perceived to lie sufficiently below their future equilibria, generating expectations of future price increases, at which point the quasi-arbitrage condition will be met. Conversely, when the real interest rate is low, as in 2001–2005 and 2008–2009, money will flow into commodities. (This is the same phenomenon that also sends money flowing to foreign currencies (the ‘carry trade’), emerging markets, and other securities.) This will continue until the prices of commodities (or the other alternative assets) are perceived to lie sufficiently above their future equilibria, generating expectations of future price decreases, so as to satisfy the speculative condition.
Under the alternative specification that leaves a possible role for bandwagon effects, we combine Equations (2') and (3) to get:
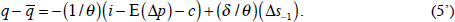
As noted, there is no reason for the net convenience yield, c, in Equation (5) to be constant. Substituting from (3) into (5),
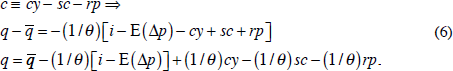
Thus, even if we continue to take the long-run equilibrium 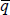 as given, there are other variables in addition to
the real interest rate that determine the real price: the convenience yield;
storage costs; and the risk premium. But
as given, there are other variables in addition to
the real interest rate that determine the real price: the convenience yield;
storage costs; and the risk premium. But 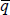 need not necessarily be constant. Fluctuations in
the convenience yield, storage costs, or the risk premium might also contain
a permanent component; all such effects would then appear in the equation.
need not necessarily be constant. Fluctuations in
the convenience yield, storage costs, or the risk premium might also contain
a permanent component; all such effects would then appear in the equation.
An additional hypothesis of interest is that storable commodities may serve as a hedge against inflation. Under this view, an increase in the expected long-run inflation rate would then raise the demand for commodities, thereby increasing real commodity prices today.[16] Adding the lagged inflation rate as a separate explanatory variable in the equation is thus another possible way of getting at the influence of monetary policy on commodity prices.
One way to isolate monetary effects on commodity prices is to look at jumps in financial markets that occur in immediate response to government announcements that change perceptions of the macroeconomic situation, as did Federal Reserve money supply announcements in the early 1980s. The experiment is interesting because news regarding disruptions to the supply of commodities and so forth is unlikely to have come out during the short time intervals in question. Frankel and Hardouvelis (1985) used Federal Reserve money supply announcements to test the monetary implications of this general theory of commodity price determination. Announcements that were interpreted as signalling tighter monetary policy indeed induced statistically significant decreases in commodity prices, and vice versa. As an alternative to the event study approach, in this paper we focus on estimating an equation for commodity price determination.
In translating Equation (6) into empirically usable form, there are several measurable determinants of the real commodity price for which we need to account. We discuss these in turn.
Inventories. Storage costs rise with the extent to which inventory holdings strain existing storage capacity: sc = Φ (INVENTORIES). If the level of inventories is observed to be at the high end historically, then storage costs must be high (absent any large recent increase in storage capacity), which has a negative effect on commodity prices.[17] Substituting into Equation (6),
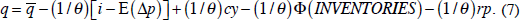
There is no reason to think that the relationship 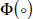 is necessarily linear. We assume linearity in our
estimation for simplicity, but allowing for non-linearity is a desirable extension
of the analysis. Under the logic that inventories are bounded below by zero
and above by some absolutely peak storage capacity, a logistic function might
be
appropriate.[18]
is necessarily linear. We assume linearity in our
estimation for simplicity, but allowing for non-linearity is a desirable extension
of the analysis. Under the logic that inventories are bounded below by zero
and above by some absolutely peak storage capacity, a logistic function might
be
appropriate.[18]
If one wished to estimate an equation for the determination of inventory holdings, one could use:
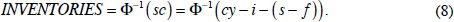
We see that low interest rates should predict not only high commodity prices but also high inventory holdings.
Economic activity (denoted Y) is a determinant of the convenience yield cy, since it drives the transactions demand for inventories. Higher economic activity should have a positive effect on the demand for inventory holdings and thus on prices; we usually proxy this with GDP. Let us designate the relationship γ (Y). Again, the assumption of linearity is arbitrary.
Medium-term volatility (denoted σ), another determinant of convenience yield cy, should have a positive effect on the demand for inventories and therefore on prices. It may also be a determinant of the risk premium. Again, we assume linearity for convenience.
Risk (political, financial and economic), in the case of oil for example, is measured by a weighted average of political risk among 12 top oil producers. (In the measures we use, a rise in the index represents a decrease in risk.) The theoretical effect on price is ambiguous. Risk is another determinant of cy (especially to the extent that risk concerns fear of disruption of availability), whereby it should have a positive effect on inventory demand and therefore on commodity prices. But it is also a determinant of the risk premium rp, whereby it should have a negative effect on commodity prices.
The spot-futures spread. Intuitively the spot-futures spread reflects the speculative return to holding inventories.[19] It is one component of the risk premium, along with expected depreciation. A higher spot-futures spread (normal backwardation), or lower futures-spot spread, signifies a low speculative return and so should have a negative effect on inventory demand and on prices.[20]
Substituting these extra effects into Equation (7), we get
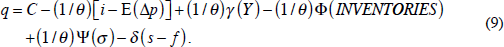
Finally, to allow for the possibility of bandwagon and bubble effects, and a separate effect of inflation on commodity prices, we can use the alternative expectations Equation (5') in place of (5). Equation (9) then becomes:
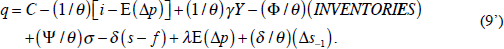
It is this equation – augmented by a hopefully well-behaved residual term – which we wish to investigate.
Each of the variables on the right-hand side of Equation (9) could easily be considered endogenous. This must be considered a limitation of our analysis. In future extensions, we would like to consider estimating three simultaneous equations: one for expectations formation, one for the inventory arbitrage condition and one for commodity price determination. However, we are short of plausibly exogenous variables with which to identify such equations. From the viewpoint of an individual commodity though, aggregate variables such as the real interest rate and GDP can reasonably be considered exogenous.[21]
3. The Dataset
We begin with a preliminary examination of the data set, starting with the commodity price series and the macroeconomic determinants of commodity prices.
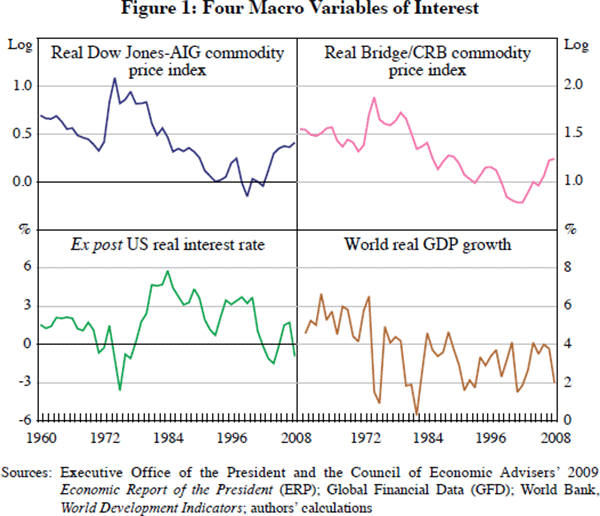
Figure 1 contains time-series plots for four variables of interest. The top pair portray the natural logarithms of two popular commodity price indices (the Dow Jones-AIG and the Bridge/CRB indices). Both series have been deflated by the US GDP chain price index to make them real. Below them are portrayed: the annualised realised US real interest rate (defined as the 3-month Treasury bill rate at auction less the percentage change in the US chain price index) and the growth rate of world real GDP (taken from the World Bank's World Development Indicators). All data are annual and span 1960 through 2008.
We follow the literature and measure commodity prices in US dollar terms and use US real interest rates. We think this is a reasonable way to proceed. If commodity markets are nationally segmented, by trade barriers and transport costs, then local commodity prices are determined by domestic real interest rates, domestic economic activity and so on. It is reasonable to assume, however, that world commodity markets are more integrated than they are segmented. Indeed, many assume that the law of one price holds closely for commodities.[22] In this case, the nominal price of wheat in Australian dollars is the nominal price in terms of US dollars multiplied by the nominal exchange rate.[23] Equivalently, the real price of wheat in Australia is the real price in the United States times the real exchange rate.[24]
Figure 1 contains few surprises. The sharp run-up in real commodity prices in the early/mid 1970s is clearly visible, as is the most recent rise. Real interest rates were low during both periods of time, and high during the early 1980s, as expected. Global business cycle movements are also clearly present in the data.
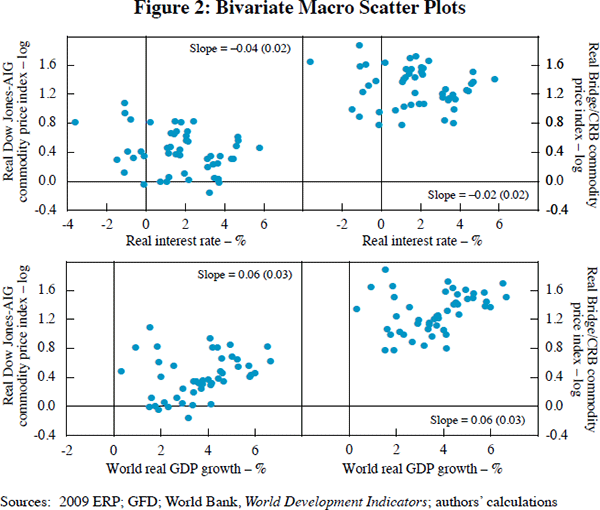
Figure 2 provides simple scatter plots of both real commodity price series against the two key macroeconomic phenomena. The bivariate relationships seem weak; real commodity prices are slightly negatively linked to real interest rates and positively to world growth. We interpret this to mean that there is plenty of room for microeconomic determinants of real commodity prices, above and beyond macroeconomic phenomena.[25] Accordingly, we now turn from aggregate commodity price indices and explanatory variables to commodity-specific data.
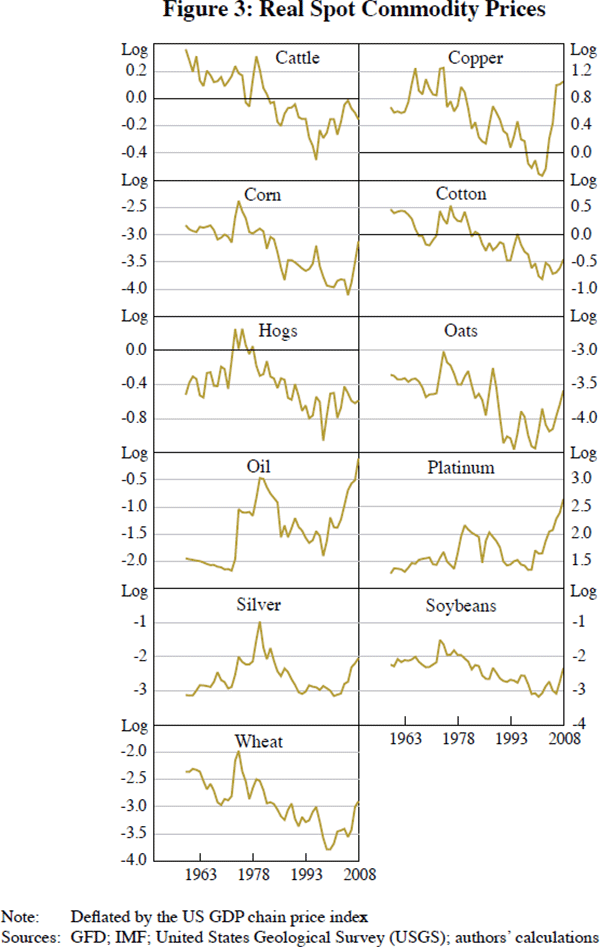
We have collected data on prices and microeconomic fundamentals for 11 commodities of interest. Seven are agricultural, including a number of crops (corn, cotton, oats, soybeans and wheat), as well as two livestock variables (live cattle and hogs). We also have oil and three non-ferrous metals (copper, platinum and silver). We chose the span, frequency, and choice of commodities so as to maximise data availability. The series are annual, and typically run from some time after the early 1960s through 2008.[26]
Figure 3 provides time-series plots of the natural logarithm of commodity prices, each deflated by the US GDP chain price index. The log of the real price shows the boom of the 1970s in most commodities and the second boom that culminated in 2008 – especially in the minerals: copper, oil and platinum.
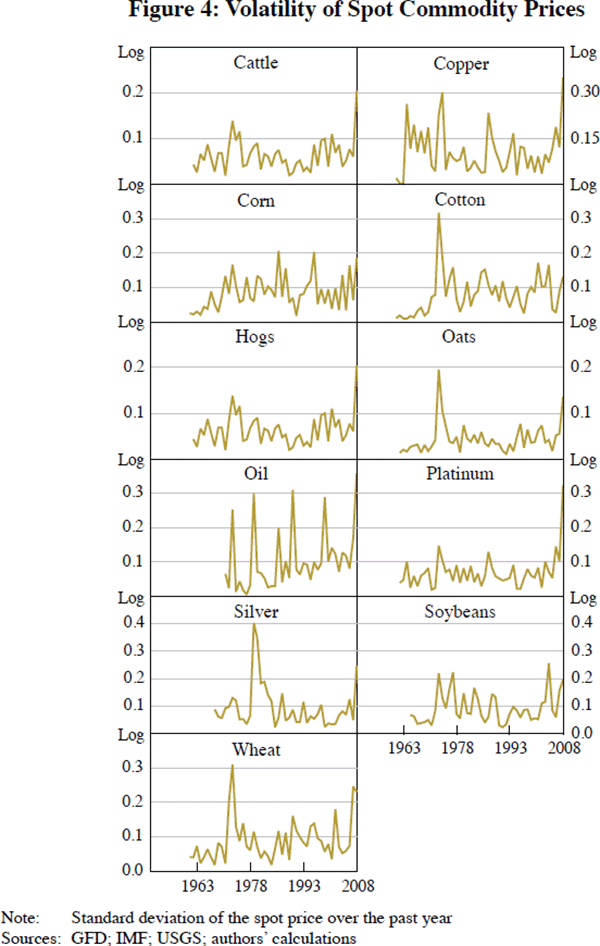
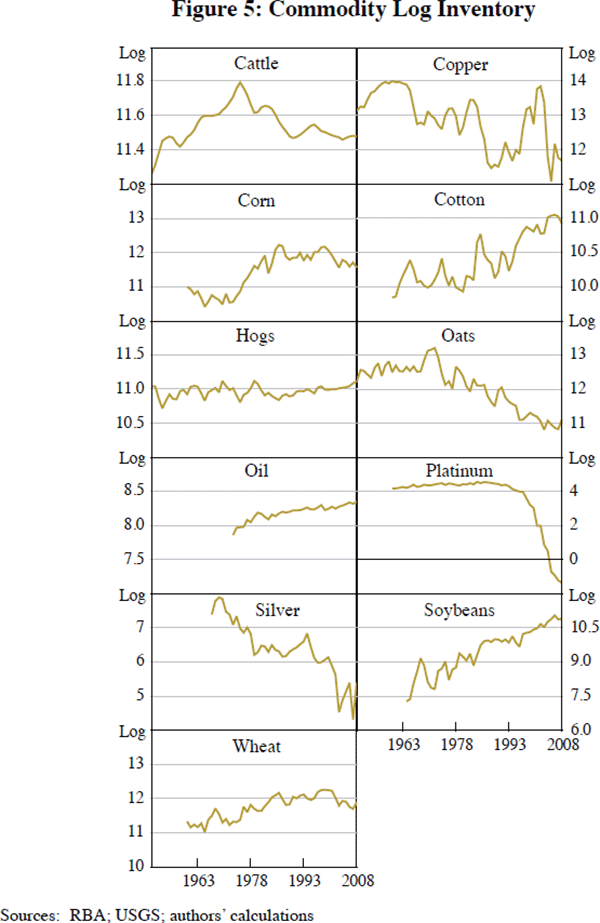
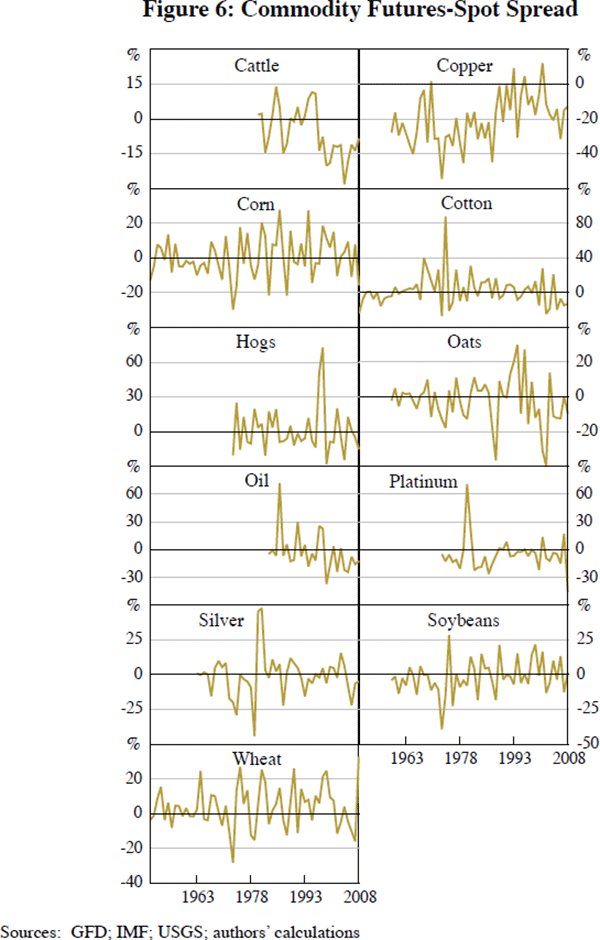
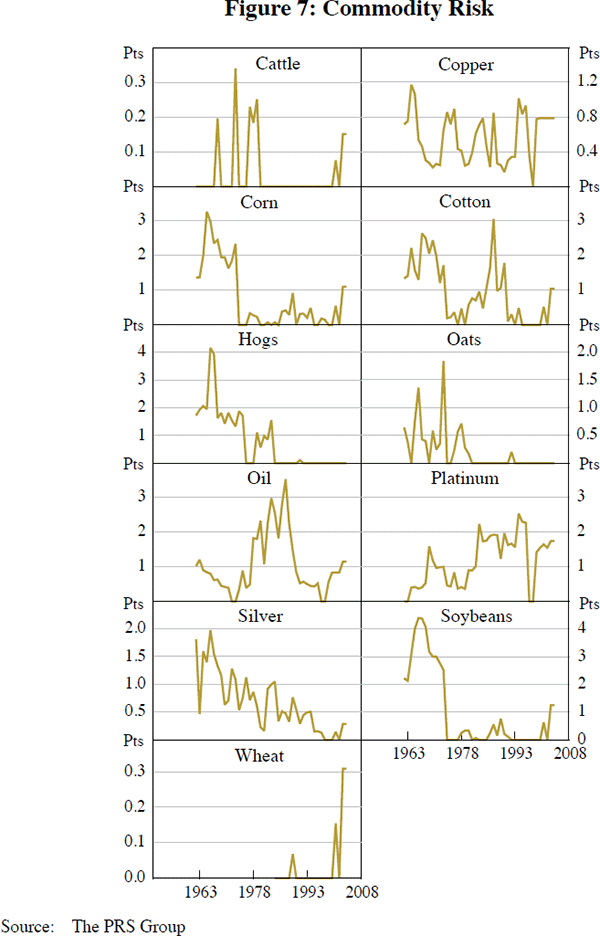
Figures 4 through 7 portray the commodity-specific fundamentals used as explanatory variables when we estimate Equation (9). We measure volatility as the standard deviation of the spot price over the past year.[27] According to our data, inventories for some commodities in 2008 were fairly high historically after all: corn, cotton, hogs, oil and soybeans.[28] The futures-spot spread alternates frequently between normal backwardation and contango. As one can see, the political risk variables are relatively limited in availability; accordingly, we do not include them in our basic equation for estimation, but use them for sensitivity analysis. Imaginative eyeballing can convince one that risks for the top oil-producing countries were high around the time of the 1973 Arab oil embargo and the aftermath of the 2001 attack on the World Trade Center.
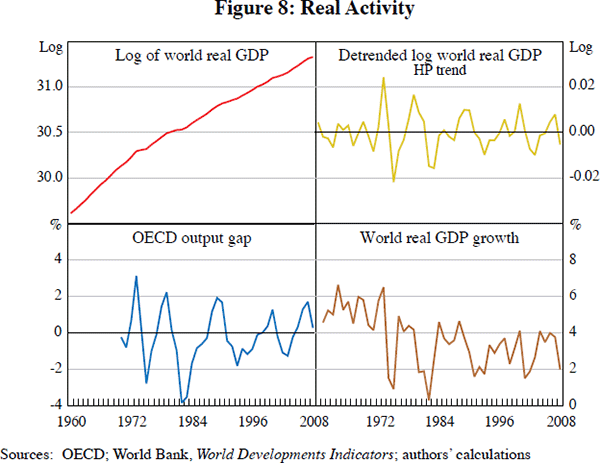
Finally, our preferred measure of real activity is plotted in Figure 8; (log) world real GDP. This has the advantage of including developing countries, including China and India. Of course all economic activity variables have positive trends. One must detrend them to be useful measures of the business cycle; we include a linear trend term in all our empirical work. (Another way to think of the trend term is as capturing the trend in supply or storage capacity, or perhaps the long-run equilibrium commodity price.) The growth rate of world GDP is also shown in Figure 8, as is world output detrended via the HP-filter. Finally, we also experiment with the output gap, which is available only for the OECD collectively, and only since 1970. In any of the measures of real economic activity one can see the recessions of 1975, 1982, 1991, 2001 and 2008.[29]
4. Estimation of the Commodity Price Determination Equation
As a warm-up, Table 1 reports the results of bivariate regressions; we show coefficients along with robust standard errors. The correlation with real economic activity is reported in the first column. Surprisingly, real prices are not significantly correlated with global output for most commodities; the exceptions are corn, oats, silver and soybeans.[30] Volatility shows a positive bivariate correlation with all prices, significantly so for nine out of eleven commodities. The correlations with the spot-futures spread and inventories are also almost always of the hypothesised sign (negative), and significant for a few commodities. The real interest rate, too, shows the hypothesised negative correlation for eight out of eleven commodity prices, but is significantly different from zero for only one commodity, hogs. Political risk is significantly different from zero in just four cases: higher political risk (a fall in our index) appears to raise demand for corn, cotton and soybeans (a negative coefficient in the last column of Table 1), but to lower it for cattle. As with volatility, the theoretical prediction is ambiguous: the positive correlation is consistent with the convenience yield effect, and the negative correlation with the risk premium effect.[31]
| World real GDP |
Volatility | Spot-futures spread | Inventories | Real interest rate | Risk | |
|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − | +/− |
| Cattle | −1.77 (1.27) |
0.10 (0.68) |
−0.007** (0.002) |
0.11 (0.41) |
−0.03 (0.02) |
1.77** (0.50) |
| Copper | −1.36 (0.85) |
2.74** (0.58) |
−0.008* (0.003) |
−0.28** (0.05) |
−0.04 (0.02) |
−0.16 (0.12) |
| Corn | −1.64** (0.59) |
2.08* (0.96) |
−0.005 (0.003) |
−0.21 (0.12) |
−0.03 (0.02) |
−0.14** (0.05) |
| Cotton | −1.35* (0.62) |
1.11** (0.39) |
−0.002 (0.002) |
−0.25 (0.13) |
0.01 (0.01) |
−0.14** (0.05) |
| Hogs | −1.66 (1.90) |
1.72* (0.67) |
−0.004** (0.001) |
0.23 (0.48) |
−0.05** (0.01) |
0.08 (0.06) |
| Oats | 1.51** (0.56) |
4.17* (1.74) |
−0.007* (0.003) |
−0.20 (0.11) |
−0.03 (0.02) |
−0.03 (0.11) |
| Oil | −1.36 (6.18) |
0.49 (1.26) |
−0.004 (0.003) |
−3.39 (4.03) |
−0.01 (0.06) |
0.16 (0.08) |
| Platinum | 3.79 (3.09) |
3.24** (0.53) |
0.000 (0.005) |
−0.17** (0.03) |
0.01 (0.02) |
0.10 (0.06) |
| Silver | 6.69** (2.26) |
425** (0.71) |
0.003 (0.008) |
−0.66** (0.22) |
0.03 (0.03) |
−0.46 (0.42) |
| Soybeans | 2.48** (0.59) |
3.33** (0.49) |
−0.007 (0.004) |
−0.07 (0.10) |
−0.03 (0.02) |
−0.10** (0.03) |
| Wheat | 3.57 (3.57) |
2.48** (0.84) |
−0.002 (0.006) |
−1.03** (0.22) |
−0.01 (0.04) |
0.63 (0.43) |
| Notes: Annual data. Each cell contains a slope coefficient from a bivariate regression of the real price on the relevant regressor, allowing for an intercept and trend.** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Regressand: log real commodity price. | ||||||
The theory made it clear that prices depend on a variety of independent factors simultaneously, so these bivariate correlations may tell us little. Accordingly, Table 2a presents the multivariate estimation of Equation (9).[32] World output now shows the hypothesised positive coefficient in nine out of the eleven commodities, and is statistically significant in four of them: cattle, corn, oats and soybeans. That is, economic activity significantly raises demand for these commodities. The coefficient on volatility is statistically greater than zero for five commodities: copper, platinum, silver, soybeans and wheat. Evidently, at least for these five goods, volatility raises the demand to hold inventories, via the convenience yield. The spread and inventories are usually of the hypothesised negative sign (intuitively, backwardation signals expected future reduction in commodity values while high inventory levels imply that storage costs are high). However, the effects are significant only for a few commodities. The coefficient on the real interest rate is of the hypothesised negative sign in seven of the eleven commodities, but significantly so only for two: cattle and hogs. Overall, the macro variables work best for cattle. They work less well for the metals than for agricultural commodities, which would be surprising except that the same pattern appeared in Frankel (2008a).
| World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | |
|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − |
| Cattle | 7.37** (1.03) |
−0.65 (0.34) |
−0.007 (0.002) |
2.37** (0.48) |
−0.06** (0.01) |
| Copper | 0.03 (0.68) |
1.92** (0.54) |
−0.005 (0.003) |
−0.21** (0.06) |
−0.03 (0.01) |
| Corn | 1.53* (0.69) |
1.52 (0.89) |
−0.003 (0.003) |
−0.18 (0.17) |
−0.01 (0.02) |
| Cotton | 0.66 (0.85) |
1.07 (0.57) |
−0.002 (0.002) |
−0.12 (0.14) |
0.01 (0.01) |
| Hogs | −0.57 (1.64) |
0.64 (0.71) |
−0.004* (0.002) |
0.18 (0.31) |
−0.03** (0.01) |
| Oats | 2.66** (0.71) |
3.28 (1.69) |
−0.006** (0.002) |
−0.59** (0.11) |
−0.02 (0.01) |
| Oil | 0.05 (8.60) |
0.57 (1.69) |
−0.003 (0.003) |
−2.52 (5.02) |
−0.01 (0.07) |
| Platinum | 1.22 (2.17) |
1.78* (0.87) |
0.002 (0.002) |
−0.21** (0.03) |
0.08** (0.01) |
| Silver | 2.69 (2.13) |
3.32** (0.73) |
0.003 (0.003) |
−0.37* (0.18) |
0.01 (0.03) |
| Soybeans | 1.94** (0.70) |
2.68** (0.55) |
−0.001 (0.002) |
−0.05 (0.07) |
−0.01 (0.01) |
| Wheat | −5.98* (2.79) |
1.90** (0.47) |
0.008* (0.003) |
−1.42** (0.27) |
0.03 (0.02) |
| Notes: Annual data. OLS, commodity by commodity (so each row represents a different regression). ** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Intercept and linear time trend included, not reported. Regressand: log real commodity price. | |||||
When the regressions are run in first differences, in Table 2b, the output coefficient is now always of the hypothesised positive sign. But the coefficient is smaller in magnitude and significant less often. Volatility is still significantly positive for five commodities, the spot-futures spread significantly negative for four, and inventories significantly negative for two. Any effect of the real interest rate has vanished.
| World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | |
|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − |
| Cattle | 0.01 (0.02) |
−0.46 (0.50) |
−0.004** (0.001) |
−1.26 (0.96) |
−0.00 (0.01) |
| Copper | 0.07** (0.02) |
0.44 (0.27) |
−0.002 (0.001) |
−0.08 (0.07) |
0.03 (0.02) |
| Corn | 0.02 (0.02) |
1.01 (0.53) |
−0.001 (0.001) |
−0.21 (0.12) |
−0.01 (0.02) |
| Cotton | 0.01 (0.02) |
1.05** (0.37) |
−0.001 (0.001) |
−0.02 (0.13) |
0.02 (0.03) |
| Hogs | 0.02 (0.03) |
−0.76 (0.85) |
−0.003** (0.001) |
−0.56 (0.50) |
−0.02 (0.02) |
| Oats | 0.03 (0.02) |
1.76* (0.71) |
−0.005** (0.001) |
−0.65** (0.12) |
−0.02 (0.02) |
| Oil | 0.10 (0.06) |
−0.34 (0.49) |
−0.003** (0.001) |
0.02 (1.24) |
−0.04 (0.04) |
| Platinum | 0.03 (0.03) |
1.28** (0.44) |
0.000 (0.001) |
−0.02 (0.07) |
0.02 (0.03) |
| Silver | 0.01 (0.04) |
1.98** (0.47) |
0.003 (0.003) |
−0.03 (0.10) |
0.01 (0.04) |
| Soybeans | 0.05** (0.02) |
1.68** (0.37) |
−0.001 (0.001) |
0.01 (0.08) |
−0.02 (0.02) |
| Wheat | 0.03 (0.04) |
0.90 (0.53) |
0.004 (0.002) |
−0.89** (0.23) |
−0.02 (0.04) |
| Notes: Annual data. OLS, commodity by commodity (so each row represents a different regression). ** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Intercept and linear time trend included, not reported. Regressand: first-difference in log real commodity price. | |||||
Analysing commodities one at a time does not produce strong evidence overall. This may not be surprising. For one thing, because we are working with annual data here, each regression has relatively few observations. For another thing, we know that we have not captured idiosyncratic forces such as the weather events that lead to bad harvests in some regions or the political unrest that closes mines in other parts of the world. We hope to learn more when we combine data from different commodities together.
Tables 3a and 3b are probably our most important findings. They combine data from different commodities into one large panel data set.[33] In the panel setting, with all the data brought to bear, the theory is supported more strongly. The basic equation, with fixed effects for each commodity, is portrayed in the first row. The coefficients on world output and volatility have the expected positive effects; the latter is significantly different from zero at the 1 per cent level, while the former misses significance by a whisker (the significance level is 5.3 per cent). The coefficients on the spread and inventories are significantly different from zero with the hypothesised negative effects; and the coefficient on the real interest rate, though not significant, is of the hypothesised negative sign. Our basic equation also fits the data reasonably; the within-commodity R2 = 0.58, though the between-commodity R2 is a much lower 0.15 (as expected). The fitted values are graphed against the actual (log real) commodity prices in the top-left panel of Figure 9. (The panel immediately to the right shows the results when the fixed effects are removed from the fitted values.)
| World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | Risk | |
|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − | +/− |
| Basic | 0.60 (0.27) |
2.29** (0.40) |
−0.003* (0.001) |
−0.15** (0.02) |
−0.01 (0.01) |
|
| Add time-fixed effects | na | 1.61** (0.29) |
−0.002* (0.001) |
−0.13** (0.01) |
na | |
| Drop spread | 0.58 (0.30) |
2.36** (0.38) |
na | −0.15** (0.02) |
−0.01 (0.01) |
|
| Add risk | 1.00** (0.23) |
1.67** (0.57) |
−0.003* (0.001) |
−0.15** (0.03) |
0.00 (0.01) |
−0.05 (0.04) |
| Growth (not log) of world real GDP | −0.01 (0.01) |
2.36** (0.40) |
−0.003 (0.001) |
−0.15** (0.02) |
−0.00 (0.01) |
|
| OECD output gap | 0.01 (0.01) |
2.34** (0.44) |
−0.002* (0.001) |
−0.15** (0.02) |
−0.01 (0.01) |
|
| HP-filtered GDP | 2.35 (1.47) |
2.32** (0.43) |
−0.003* (0.001) |
−0.14** (0.02) |
−0.01 (0.01) |
|
| Add quadratic trend | 0.48 (0.40) |
2.30** (0.40) |
−0.003* (0.001) |
−0.15** (0.02) |
−0.01 (0.01) |
|
| Notes: Annual data.** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Commodity-specific fixed intercepts and trend included, not reported. Regressand: log real commodity price. | ||||||
| World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | Risk | |
|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − | +/− |
| Basic | 0.03** (0.01) |
0.75** (0.24) |
−0.002** (0.001) |
−0.10* (0.05) |
0.00 (0.01) |
|
| Add time-fixed effects | na | 0.53** (0.18) |
−0.002** (0.001) |
−0.07 (0.04) |
na | |
| Drop spread | 0.04** (0.01) |
na | −0.0020** (0.0005) |
−0.10 (0.05) |
−0.00 (0.01) |
|
| Add risk | 0.03** (0.01) |
0.65* (0.28) |
−0.0018** (0.0005) |
−0.15* (0.07) |
0.01 (0.01) |
−0.03 (0.02) |
| OECD output gap | 0.03** (0.01) |
0.77* (0.25) |
−0.0018** (0.0005) |
−0.12* (0.04) |
0.01 (0.01) |
|
| HP-filtered GDP | 4.91** (0.97) |
0.78* (0.23) |
−0.002** (0.001) |
−0.12* (0.04) |
0.01 (0.01) |
|
| Add quadratic trend | 0.03** (0.01) |
0.75** (0.24) |
−0.002** (0.001) |
−0.10* (0.05) |
0.00 (0.01) |
|
| Notes: Annual data.** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Commodity-specific fixed intercepts and trend included, not reported. Regressand: log real commodity price first-difference. | ||||||
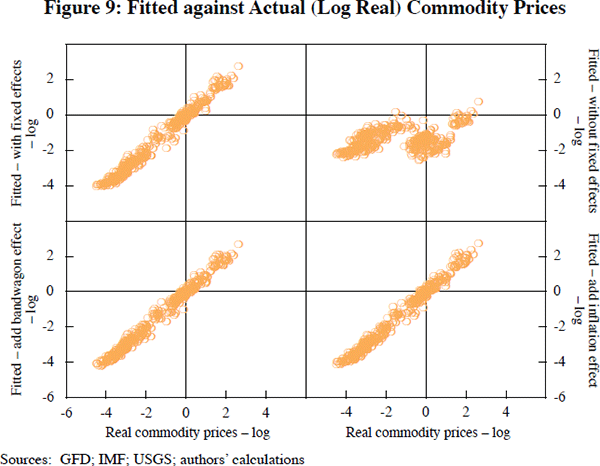
Table 3a also reports a variety of extensions and sensitivity tests in the lower rows. The second row of results adds year-specific effects to commodity-specific fixed effects. The two macroeconomic variables, world output and the real interest rate, necessarily drop out in the presence of these time-fixed effects; by definition they do not vary within a cross-section of commodities. But it is reassuring that the three remaining (microeconomic) variables – volatility, the spread, and inventories – retain their significant effects. The next row drops the spot-futures spread from the specification on the grounds that its role may already be played by inventories (see Equation (7)). The effects of inventories and the other variables remain essentially unchanged. Next, we add the political risk variable back in. It is statistically insignificant, but in its presence the world output variable becomes more significant than ever. We then try four alternative measures of global economic activity in place of the log of world real GDP: (1) the growth rate of world real GDP; (2) the OECD output gap; (3) Hodrick-Prescott filtered GDP; and (4) log world real GDP with a quadratic trend. None works as well as the level of real GDP, but the microeconomic effects are essentially unchanged.
Table 3b repeats the exercise of Table 3a, but using first differences rather than (log) levels, with similar results. In particular, the signs for the microeconomic determinants are almost always as hypothesised, as is the effect of economic activity. Most of the coefficients are also significantly different from zero, though the effect of activity on commodity prices is much smaller than in Table 3a. The estimated effects of real interest rates are often positive, although never significant.
Table 4 retains the panel estimation technique of Tables 3a and 3b, but reports the outcome of adding the rate of change of the spot commodity price over the preceding year to the standard list of determinants. The rationale is to test the theory of destabilising speculation by looking for evidence of bandwagon effects, as in Equation (9'). The lagged change in the spot price is indeed highly significant statistically, even if time-fixed effects are added, data after 2003 are dropped, or auto-correlated residuals are included in the estimation. It is also significant regardless of whether the spread or political risk variables are included or not, and regardless of the measure of economic activity. Evidently, alongside the regular mechanism of regressive expectations that is implicitly built into the basic model (a form of stabilising expectations), the results in Table 4 show that there is also a mechanism of extrapolative expectations (which is capable of producing self-confirming bubble effects).
| World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | Risk | Lagged nominal change | |
|---|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − | +/− | |
| Basic | 0.50 (0.27) |
1.84** (0.40) |
−0.004** (0.001) |
−0.13** (0.02) |
0.00 (0.01) |
0.0061** (0.0005) |
|
| Add time-fixed effects | na | 1.37** (0.28) |
−0.004** (0.001) |
−0.12** (0.01) |
na | 0.0050** (0.0008) |
|
| Drop spread | 0.48 (0.32) |
2.01** (0.37) |
na | −0.14** (0.02) |
−0.00 (0.01) |
0.0053** (0.0005) |
|
| Add risk | 0.93** (0.24) |
1.25 (0.58) |
−0.004** (0.001) |
−0.13** (0.03) |
0.01 (0.01) |
−0.03 (0.04) |
0.0050** (0.0005) |
| Growth (not log) of world real GDP | −0.01 (0.01) |
1.90** (0.40) |
−0.005** (0.001) |
−0.13** (0.02) |
0.01 (0.01) |
0.0061** (0.0005) |
|
| OECD output gap | −0.00 (0.01) |
1.90** (0.43) |
−0.004** (0.001) |
−0.13** (0.02) |
0.01 (0.01) |
0.0063** (0.0005) |
|
| HP-filtered GDP | −0.71 (1.58) |
1.92** (0.42) |
−0.004** (0.001) |
−0.13** (0.02) |
0.01 (0.01) |
0.0062** (0.0005) |
|
| Add quadratic trend | 0.26 (0.37) |
1.85** (0.41) |
−0.004** (0.001) |
−0.13** (0.02) |
0.01 (0.01) |
0.0062** (0.0005) |
|
| Drop post-2003 data | 1.21** (0.28) |
1.26 (0.58) |
−0.004** (0.001) |
−0.11** (0.04) |
0.01 (0.01) |
0.0049** (0.0005) |
|
| With AR(1) residuals | 2.08* (0.81) |
0.89** (0.13) |
−0.0033** (0.00004) |
−0.10** (0.03) |
0.00 (0.01) |
0.0031** (0.0004) |
|
| Notes: Annual data.** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Commodity-specific fixed intercepts and trend included, not reported. Regressand: log real commodity price. ‘Lagged nominal change’ is coefficient for lagged percentage change in nominal spot commodity price. | |||||||
Table 5 reports the result of adding a separate coefficient for the US inflation
rate, above and beyond the real interest rate (and the other standard commodity
price determinants). Thus there are two separate measures of the monetary policy
stance. Recall that the hypothesised role of the real interest rate is to pull
the current real commodity price q away from its long-run equilibrium 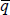 ,
while the role of the expected inflation rate is to raise
,
while the role of the expected inflation rate is to raise 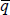 to the extent that commodities are considered useful as a hedge against inflation.
In our default specification, and under almost all of the variations, the coefficient
on inflation is greater than zero and highly significant. The result suggests
that commodities are indeed valued as a hedge against inflation. The positive
effect of inflation offers a third purely macroeconomic explanation for commodity
price movements (alongside real interest rates, which do not work very well
in our results, and growth, which does).[34],[35]
to the extent that commodities are considered useful as a hedge against inflation.
In our default specification, and under almost all of the variations, the coefficient
on inflation is greater than zero and highly significant. The result suggests
that commodities are indeed valued as a hedge against inflation. The positive
effect of inflation offers a third purely macroeconomic explanation for commodity
price movements (alongside real interest rates, which do not work very well
in our results, and growth, which does).[34],[35]
| World real GDP | Volatility | Spot-futures spread | Inventories | Risk | Real interest rate | Inflation | |
|---|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | +/− | − | + |
| Basic | −2.11** (0.61) |
2.12** (0.27) |
−0.0032** (0.0007) |
−0.14** (0.02) |
0.019 (0.012) |
0.082** (0.015) |
|
| Drop spread | −2.04** (0.63) |
2.21** (0.26) |
na | −0.15** (0.02) |
0.015 (0.012) |
0.079** (0.015) |
|
| Add risk | −1.25* (0.44) |
1.57** (0.44) |
−0.0031** (0.0006) |
−0.14** (0.02) |
−0.02 (0.04) |
0.020 (0.014) |
0.067** (0.015) |
| Growth (not log) of world real GDP | 0.02 (0.01) |
2.01** (0.32) |
−0.0027** (0.0007) |
−0.15** (0.02) |
0.006 (0.011) |
0.058** (0.010) |
|
| OECD output gap | −0.00 (0.01) |
2.09** (0.28) |
−0.0030** (0.0007) |
−0.15** (0.02) |
0.014 (0.012) |
0.083** (0.014) |
|
| HP-filtered GDP | 0.19 (1.64) |
2.03** (0.33) |
−0.0031** (0.0008) |
−0.15** (0.02) |
0.005 (0.013) |
0.051** (0.009) |
|
| Add quadratic trend | −2.47** (0.76) |
2.14** (0.27) |
−0.0032** (0.0006) |
−0.14** (0.02) |
0.017 (0.011) |
0.085** (0.015) |
|
| Notes: Annual data.** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Commodity-specific fixed intercepts and trend included, not reported. Regressand: log real commodity price. | |||||||
Tables 6a and 6b report the results for a variety of aggregate commodity price indices that we have created. Prices and each of the relevant determinant variables have been aggregated using commodity-specific data and (time-invariant) weights from a particular index. We use weights from five popular indices (Dow Jones-AIG; S&P GSCI; Bridge/CRB; Grilli-Yang; and The Economist), and also create an equally weighted index. Since these rely on a number of commodities for which we do not have data, our constructed indices are by no means equal to the original indices (such as those portrayed in Figures 1 and 2). Further, the span of data available over time varies by commodity. Accordingly, we create three different indices for each weighting scheme; the narrowest (in that it relies on the fewest commodities) stretches back to 1964, while broader indices are available for shorter spans of time (we create indices that begin in 1973 and 1984). We use the same weights for prices and their fundamental determinants. The benefit from this aggregation is that some of the influences that are particular to individual commodities, such as weather, may wash out when we look at aggregate indices. The cost is that we are left with many fewer observations.
| Period after | World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | |
|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − | |
| Dow Jones-AIG | 1984 | 3.52 (2.24) |
1.33** (0.16) |
−0.003 (0.002) |
−0.21 (0.19) |
−0.01 (0.02) |
| 1973 | 2.11 (1.13) |
1.32** (0.11) |
0.000 (0.002) |
−0.30* (0.13) |
−0.01 (0.01) |
|
| 1964 | 0.44 (0.77) |
1.28** (0.15) |
−0.003 (0.002) |
−0.11 (0.13) |
−0.01 (0.01) |
|
| S&P GSCI | 1984 | 4.83 (2.78) |
0.17 (0.35) |
−0.004** (0.001) |
1.01** (0.31) |
−0.01 (0.04) |
| 1973 | 2.18 (1.14) |
1.29** (0.10) |
−0.000 (0.002) |
−0.28* (0.13) |
−0.01 (0.01) |
|
| 1964 | 0.42 (0.75) |
1.31** (0.15) |
−0.003 (0.002) |
−0.17 (0.13) |
−0.01 (0.01) |
|
| Bridge/CRB | 1984 | 3.64 (2.58) |
0.99** (0.23) |
−0.003 (0.002) |
0.09 (0.25) |
−0.01 (0.03) |
| 1973 | 2.24 (1.31) |
1.27** (0.10) |
−0.000 (0.001) |
−0.25 (0.13) |
−0.01 (0.01) |
|
| 1964 | 0.47 (0.71) |
1.32** (0.15) |
−0.003 (0.002) |
−0.16 (0.13) |
−0.01 (0.01) |
|
| Grilli-Yang | 1984 | 3.83 (2.64) |
1.42** (0.14) |
−0.002 (0.002) |
−0.25 (0.14) |
−0.01 (0.02) |
| 1973 | 2.61 (1.76) |
1.18** (0.13) |
−0.001 (0.002) |
−0.17 (0.16) |
−0.01 (0.01) |
|
| 1964 | 0.32 (0.67) |
1.27** (0.17) |
−0.003 (0.002) |
−0.18 (0.13) |
−0.01 (0.01) |
|
| The Economist | 1984 | 3.76 (2.55) |
1.39** (0.11) |
−0.002 (0.002) |
−0.22 (0.12) |
−0.01 (0.02) |
| 1964 | 0.37 (0.72) |
1.29** (0.16) |
−0.003 (0.002) |
−0.14 (0.12) |
−0.01 (0.01) |
|
| Equally weighted | 1984 | 3.26 (1.76) |
1.64** (0.16) |
−0.003 (0.002) |
−0.50** (0.16) |
−0.01 (0.02) |
| 1973 | 2.09 (1.22) |
1.36** (0.15) |
−0.000 (0.002) |
−0.36* (0.15) |
−0.01 (0.01) |
|
| 1964 | 0.43 (0.61) |
1.40** (0.17) |
−0.003 (0.002) |
−0.26 (0.13) |
−0.01 (0.01) |
|
| Notes: Annual data. ** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Intercept and trend included, not reported. Price indices and micro-determinants are weighted averages (according to different schemes). Regressand: constructed log real commodity price index. | ||||||
| Period after | World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | |
|---|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − | |
| Dow Jones-AIG | 1984 | 0.07** (0.02) |
0.22 (0.48) |
0.002 (0.001) |
−0.35* (0.14) |
−0.02 (0.02) |
| 1973 | 0.03* (0.01) |
1.55** (0.39) |
0.000 (0.002) |
−0.29* (0.12) |
−0.00 (0.02) |
|
| 1964 | 0.04** (0.01) |
1.98** (0.49) |
−0.002 (0.002) |
−0.09 (0.11) |
0.00 (0.01) |
|
| S&P GSCI | 1984 | 0.10* (0.04) |
−0.24 (0.44) |
−0.002* (0.001) |
−0.66 (0.66) |
−0.04 (0.03) |
| 1973 | 0.03* (0.02) |
1.20* (0.44) |
0.000 (0.002) |
−0.29* (0.14) |
−0.00 (0.02) |
|
| 1964 | 0.04* (0.02) |
1.81** (0.50) |
−0.002 (0.002) |
−0.13 (0.11) |
0.00 (0.01) |
|
| Bridge/CRB | 1984 | 0.08** (0.03) |
−0.21 (0.43) |
−0.002 (0.001) |
−0.43* (0.19) |
−0.03 (0.02) |
| 1973 | 0.03 (0.02) |
1.35** (0.42) |
0.000 (0.002) |
−0.25 (0.13) |
0.00 (0.02) |
|
| 1964 | 0.03** (0.01) |
1.87** (0.45) |
−0.002 (0.002) |
−0.12 (0.10) |
0.01 (0.01) |
|
| Grilli-Yang | 1984 | 0.03* (0.02) |
1.50* (0.61) |
−0.001 (0.002) |
−0.22 (0.13) |
0.02 (0.02) |
| 1973 | 0.03 (0.02) |
1.60** (0.42) |
−0.001 (0.002) |
−0.17 (0.14) |
0.02 (0.02) |
|
| 1964 | 0.03 (0.02) |
1.25** (0.39) |
−0.002 (0.002) |
−0.12 (0.12) |
0.02 (0.01) |
|
| The Economist | 1984 | 0.03* (0.02) |
2.13** (0.66) |
−0.001 (0.001) |
−0.20* (0.10) |
0.02 (0.02) |
| 1964 | 0.04** (0.01) |
1.79** (0.41) |
−0.002 (0.002) |
−0.10 (0.10) |
0.01 (0.01) |
|
| Equally weighted | 1984 | 0.06* (0.02) |
1.59** (0.50) |
−0.003 (0.002) |
−0.35** (0.09) |
0.00 (0.02) |
| 1973 | 0.03 (0.02) |
1.84** (0.48) |
0.000 (0.002) |
−0.35* (0.13) |
0.00 (0.02) |
|
| 1964 | 0.03* (0.01) |
1.93** (0.46) |
−0.002 (0.002) |
−0.22 (0.11) |
0.00 (0.01) |
|
| Notes: Annual data. ** (*) means significantly different from zero at the 1 and 5 per cent levels respectively. Robust standard errors in parentheses. Intercept and trend included, not reported. Price indices and micro-determinants are weighted averages (according to different schemes). Regressand: constructed first-difference log real commodity price index. | ||||||
In the first column of Table 6a – which reports results in levels – the real GDP output coefficient always has the hypothesised positive sign. However, it is only significant in Table 6b, where the estimation is in terms of first differences. The volatility coefficient is almost always statistically greater than zero in both Tables 6a and 6b. The coefficient on the spot-futures spread is almost always negative, but not usually significantly different from zero. The inventory coefficient is also almost always negative, and sometimes significant. The real interest rate is never significant, though the sign is generally negative (and always negative in Table 6a). The lack of statistical significance probably arises because now that we are dealing with short time series of aggregate indices, the number of observations is smaller than in the panel analysis; this is especially true in the cases where we start the sample later.
Although we have already reported results of regressions run in both levels and first differences, a complete analysis requires that we examine the stationarity or non-stationarity of the series more formally. Tables in Appendix A tabulate Phillips-Perron tests for unit roots in our individual variables; the aggregate series are handled in Table A1a, while the commodity-specific results are in Table A1b. Table A1c is the analogue that tests for common panel unit roots. The tests often fail to reject unit roots (though not for the spread and volatility). One school of thought would doubt, on a priori grounds, that variables such as the real interest rate could truly follow a random walk. The other school of thought says that one must go wherever the data instruct. Here we pursue the implication of unit roots to be safe, as a robustness check if nothing else. However, we are reluctant to over-interpret our results, especially given the limited number of time-series observations.[36]
Tables A2a–A2c report related tests of cointegration. We generally find cointegration in commodity-specific models, but have weaker results in our panel cointegration result. It is not clear to us whether this is the result of low power, the absence of fixed effects or some other misspecification. Still, Table A3 reports results from commodity-specific vector error correction models (VECMs). As in some of the previous tests, the three variables that are most consistently significant and of the hypothesised sign are the volatility, the spread and inventories. We view this as a reassuring corroboration of the panel estimation we have already documented.
5. Summary and Conclusion
This paper has presented a model that can accommodate each of the prominent explanations that were given for the run-up in prices of most agricultural and mineral commodities that culminated in the 2008 spike: global economic activity, easy monetary policy, and destabilising speculation. Our model includes both macroeconomic and microeconomic determinants of real commodity prices.
The theoretical model is built around the ‘arbitrage’ decision faced by any firm holding inventories. This is the trade-off between the cost of carrying the inventory on the one hand (the interest rate plus the cost of storage) versus the convenience yield and spot-futures spread (or, if unhedged, the expected capital gain adjusted for the risk premium) on the other hand. A second equation completes the picture; the real commodity price is expected to regress gradually back to its long-run equilibrium (at least absent bandwagon effects). The reduced-form equation expresses the real commodity price as a function of the real interest rate, storage costs, convenience yield and the risk premium. The level of inventories is a ready stand-in for storage costs. The empirical significance of the inventory variable suggests that the data and relationship are meaningful, notwithstanding fears that the available measures of inventories are incomplete.[37] Global economic activity is an important determinant of the convenience yield. Measures of political risk and price uncertainty are other potentially important determinants of both convenience yield and the risk premium.
Our strongest results come about when we bring together as much data as possible, in the panel estimates of Tables 3a, 3b, 4 and 5. Our annual empirical results show support for the influence of economic activity, inventories, uncertainty, the spread and recent spot price changes. The significance of the inventories variable supports the legitimacy of arguments by others who have used observed inventory levels to gauge the roles of speculation or interest rates. There was little support in these new annual results for the hypothesis that easy monetary policy and low real interest rates are an important source of upward pressure on real commodity prices, beyond any effect they might have via real economic activity and inflation. (This result differs from more positive results of previous papers.) We also find evidence that commodity prices are driven in part by bandwagon effects and by inflation per se.
A number of possible extensions remain for future research. These include: (1) estimation at monthly or quarterly frequency (the big problem here is likely to be data availability, especially for any reasonably long span of time); (2) testing for nonlinearity in the effects of growth, uncertainty and (especially) inventories; (3) using implicit volatility inferred from commodity options prices as the measure of uncertainty; (4) using survey data to measure commodity price expectations explicitly; and (5) simultaneous estimation of the three equations: expectations formation (regressive versus bandwagon), the inventory arbitrage condition, and the equation for determination of the real commodity price. The future agenda remains large.
What caused the run-up in commodities prices in the 2000s? One explanation is the recent rapid global growth – as in the 1970s – aided now by China and India. Presumably, then the abrupt decline in the latter part of 2008, and even the partial recovery in the spring of 2009, could be explained by the rapidly evolving prospects for the real economy. But this story is still not able to explain the acceleration of commodity prices between mid 2007 and the peak around the second half of 2008, a time when growth prospects were already being downgraded in response to the US sub-prime mortgage crisis. Of the two candidate theories to explain that interval – low real interest rates and a speculative bubble – there is more support for the latter in this paper, in the form of bandwagon effects. But a more definitive judgment on both may have to await higher-frequency data.
Appendix A: Predictive Bias in Commodity Futures Markets
This Appendix briefly reviews the literature on whether forward and futures prices are unbiased forecasts of future spot prices for commodities, and – where there is systematic bias – what the source might be.
Commodity futures can deliver both storage facilitation and a forward-pricing role in their price discovery function.[38] Accordingly, there are two main theories in commodity futures price determination:
- The theory of storage or costs-of-carry models (Working 1949; Brennan 1958), which explain the difference in the contemporaneous spot price and futures price of commodities by the net costs of carrying stock. These are composed of: (1) interest foregone (had they been sold earlier); (2) warehousing costs; and (3) the convenience yield.
- The view that the futures price has two components (Breeden 1980; Hazuka 1984): the expected risk premium (Keynes' ‘normal backwardation theory’) and the forecast of future spot price. Under this theory, the futures price is a biased estimate of future spot price because of the risk premium – insurance being sold by the speculators to the hedgers.
Is the Futures Price a Biased Predictor of the Future Spot Price?
Some studies address the question of the unbiasedness of futures prices (in forecasting spot prices) by examining the cointegration between futures and spot prices; this allows one to deal with problems of the non-stationary nature of commodities prices (for example, Covey and Bessler 1995; Brenner and Kroner 1995; Fortenbery and Zapata 1998; and Yang et al 2001). Moosa and Al-Loughani (1994) and Chernenko, Schwarz and Wright (2004) find bias. Similarly, Morana (2001) finds that forward rates for oil actually point in the wrong direction more often than not. Chinn, LeBlanc and Coibion (2005), however, do not find bias in energy futures, while Green and Mork (1991) have mixed results for oil.
Many studies are motivated by the presumed existence of a risk premium in the futures price. The evidence is mixed. For example, Bessembinder (1993) found evidence of non-trivial risk premia for live cattle, soybeans and cotton, but much smaller risk premia in non-agricultural assets such as T-bills. Gorton and Rouwenhorst (2006) and Gorton, Hayashi and Rouwenhorst (2007) find systematic components to commodity returns. On the other hand, Fama and French (1987) studied 21 commodities and found only weak evidence of time-varying risk premia. A study by Kolb (1992) did not find evidence of risk premia for most of the 29 commodities examined. Many of these studies, however, equated the risk premium to the extra returns earned by speculators during particular sample periods, in other words by defining the risk premium as observed bias in the futures price as a forecast of the future spot price. These studies tend to neglect the question of whether the bias in the futures price might come from systematic prediction errors in-sample, rather than from a time-varying risk premium.
Is the Bias a Risk Premium or Expectational Errors?
Choe (1990) attempted to bring an independent expectations measure to bear on the question of whether the predictive bias in commodity futures is due to a risk premium or to a failure of the rational expectations methodology, analogous to the approach taken by Froot and Frankel (1989) for the foreign exchange market. To test this for commodities (including cocoa, coffee, copper, cotton, maize, soybeans, sugar and wheat), Choe obtained the data on futures prices and then approximated expectations of the future spot price using the forecast conducted by the World Bank International Commodity Markets Division. He discovered that:
- using futures prices for short-term price forecasting is more bias-prone than relying on specialists' forecasts;
- in contrast to the results found by Froot and Frankel (1989), a major part of futures forecast bias comes from risk premia as well as expectational errors. For cocoa, copper, cotton and soybeans, the expectational errors seem to play a principal role, whereas the existence of risk premia is important for the other commodities;
- the size of the risk premia can be large compared to the expectational errors. However, the variance of risk premium is larger than that of the expected price change only for coffee and wheat; and
- the estimated bias from the risk premium is negative while that from expectational errors is mixed – negative for half of the commodities examined and positive for the others.
| Authors | Sources |
|---|---|
| Dusak (1973) | United States Department of Agriculture |
| Fama and French (1987) | Chicago Board of Trade (CBOT) for broilers, corn, plywood, soy oil, soybeans,
wheat Chicago Mercantile Exchange for cattle, hogs, lumber, pork bellies Commodity Exchange for copper, gold, and silver Coffee, Sugar and Cocoa Exchange for cocoa and coffee New York Cotton Exchange for cotton New York Mercantile Exchange for platinum |
| Choe (1990) | World Bank, International Economics Department and DRICOM commodity database of Data Resources Inc: cocoa, coffee, copper, cotton, maize, sugar, soybeans, wheat |
| Tomek (1997) | CBOT |
| Carter (1999) | Commodity Futures Trading Commission for both cash and futures prices |
| Yang et al (2001) | Datastream International: data on CBOT and Minneapolis Grain Exchange |
| Z(ρ) | Z(t) (MacKinnon p-value) |
|
|---|---|---|
| Log world real GDP | −0.81 | −3.85** (0.00) |
| World growth rate | −20.8** | −3.59** (0.01) |
| OECD output gap | −19.1* | −3.34* (0.01) |
| Log world real GDP – HP trend | −31.9** | −4.84** (0.00) |
| Real interest rate | −10.00 | −2.18 (0.21) |
| Notes: Annual data. ** (*) indicates rejection of null hypothesis of unit root at the 1 and 5 per cent significance levels respectively. Intercept included. Two lags as controls. | ||
| Log real price | Spread | Log inventory | Volatility | Risk | |
|---|---|---|---|---|---|
| Cattle | −7.0/−2.2 | −12.3/−2.7 | −7.5/−2.7 | −39**/−4.5** | −34**/−5.1** |
| Copper | −7.4/−1.8 | −40**/−5.5** | −8.6/−2.0 | −39**/−5.2** | −22**/−3.7** |
| Corn | −5.8/−1.8 | −61**/−8.6** | −2.6/−1.2 | −53**/−6.7** | −6.2/−1.8 |
| Cotton | −4.4/−1.6 | −77**/−10** | −4.5/−1.5 | −24**/−4.1** | −11.7/−2.6 |
| Hogs | −8.3/−2.1 | −34**/−6.2** | −23**/−3.5** | −39**/−4.5 | −7.11/2.0 |
| Oats | −7.7/−2.0 | −46**/−6.2** | −2.1/−0.8 | −30**/−4.2** | −29**/−4.7** |
| Oil | −2.6/−0.8 | −27**/−5.1** | −5.0/−3.4* | −38**/−4.9** | −7.8/−2.0 |
| Platinum | −3.2/−0.8 | −29**/−4.6** | 4.6/3.6 | −40**/−3.6** | −13.4*/−2.9* |
| Silver | −7.3/−1.9 | −35**/−5.4** | −3.1/−1.3 | −19.7**/−3.3* | −14.7*/−3.3* |
| Soybeans | −5.4/−1.7 | −56**/−8.1** | −4.2/−1.8 | −24**/−4.0** | −3.9/−1.5 |
| Wheat | −6.6/−2.0 | −49**/−6.5** | −5.0/−1.7 | −28**/−4.2** | −5.3/−1.1 |
| Notes: Z(ρ)/Z(t) statistics reported. Annual data. ** (*) indicates rejection of null hypothesis of unit root at the 1 and 5 per cent significance levels respectively. Intercept included. Two lags as controls. | |||||
| Im, Pesaran, Shin (p-value) |
Levin, Lin |
Dickey, Fuller |
Maddala, Wu |
|
|---|---|---|---|---|
| Log real price | −1.79 (0.13) |
−0.14 (0.28) |
65 | 13.2 (0.93) |
| Risk | −1.73 (0.16) |
−0.34* (0.01) |
307 | 20.6 (0.55) |
| Spread | −2.83** (0.00) |
−0.98* (0.03) |
136 | 83.6** (0.00) |
| Log inventory | −1.05 (0.94) |
−0.06 (0.95) |
85 | 27.4 (0.20) |
| Volatility | −3.05** (0.00) |
−0.84 (0.09) |
144 | 58.4** (0.00) |
| Notes: Annual data. ** (*) indicates rejection of null hypothesis of unit root at the 1 and 5 per cent significance levels respectively. Intercept included. Two lags as controls. | ||||
| Basic | 1% level |
3 lags | Add trend |
Add risk |
Drop spread |
|
|---|---|---|---|---|---|---|
| Cattle | 4 | 3 | 5 | 6 | 2 | |
| Copper | 0 | 0 | 1 | 0 | 1 | 1 |
| Corn | 2 | 1 | 2 | 5 | 2 | |
| Cotton | 3 | 1 | 0 | 3 | 2 | |
| Hogs | 2 | 1 | 4 | 3 | 4 | 2 |
| Oats | 2 | 1 | 1 | 2 | 2 | 2 |
| Oil | 3 | 3 | 4 | 2 | ||
| Platinum | 2 | 1 | 3 | 1 | 3 | 1 |
| Silver | 1 | 1 | 3 | 2 | 1 | 0 |
| Soybeans | 2 | 2 | 4 | 2 | 2 | 1 |
| Wheat | 3 | 2 | 5 | 2 | 2 | |
| Notes: Maximal rank from Johansen trace statistic at 5 per cent level unless noted. Annual data. Intercept included. Two lags included unless noted. Model of log real commodity price includes five controls (spread, log inventory, volatility, real interest rate, log world real GDP) unless noted. | ||||||
| Gt | Ga | Pt | Pa | |
|---|---|---|---|---|
| Basic | −1.31 (1.00) |
−2.47 (1.00) |
−4.53 (0.92) |
−2.70 (0.99) |
| Only 1 lag | −1.88 (0.85) |
−3.02 (1.00) |
−4.97 (0.85) |
−3.32 (0.98) |
| Add constant | −1.41 (1.00) |
−3.74 (1.00) |
−4.28 (1.00) |
−3.47 (1.00) |
| Add constant, trend | −1.31 (1.00) |
−3.32 (1.00) |
−3.97 (1.00) |
−3.08 (1.00) |
| Add lead | −0.46 (1.00) |
−0.57 (1.00) |
−2.34 (1.00) |
−0.87 (1.00) |
| Notes: Basic: two lags. p-values (for null hypothesis of no cointegration) recorded in parentheses. Model of log real commodity price includes five controls (spread, log inventory, volatility, real interest rate, log world real GDP). | ||||
| Gt | Ga | Pt | Pa | |
|---|---|---|---|---|
| Basic | −1.66 (0.85) |
−2.70 (1.00) |
−4.12 (0.69) |
−3.07 (0.92) |
| Only 1 lag | −1.87 (0.64) |
−5.36 (0.98) |
−5.14 (0.57) |
−4.54 (0.76) |
| Add constant | −1.51 (1.00) |
−5.31 (1.00) |
−4.00 (1.00) |
−3.34 (1.00) |
| Add constant, trend | −1.84 (1.00) |
−6.88 (1.00) |
−4.84 (1.00) |
−4.22 (1.00) |
| Add lead | −1.07 (1.00) |
−2.33 (1.00) |
−3.28 (0.95) |
−1.79 (0.98) |
| Notes: Basic: two lags. p-values (for null hypothesis of no cointegration) recorded in parentheses. Model of log real commodity price includes six controls (risk, spread, log inventory, volatility, real interest rate, log world real GDP). | ||||
| World real GDP | Volatility | Spot-futures spread | Inventories | Real interest rate | |
|---|---|---|---|---|---|
| Hypothesised sign on coefficient | + | + | − | − | − |
| Cattle | 6.20** (1.76) |
−72** (10.0) |
−0.095** (0.023) |
17.2** (6.6) |
0.08 (0.17) |
| Copper | 0.99** (0.27) |
−0.37 (1.54) |
−0.076** (0.007) |
−0.40* (0.16) |
−0.04 (0.05) |
| Corn | −0.28 (0.21) |
3.65** (1.04) |
−0.056** (0.004) |
−0.47* (0.20) |
0.03 (0.03) |
| Cotton | −092** (0.19) |
5.75** (0.95) |
−0.054** (0.003) |
−0.91** (0.24) |
0.01 (0.03) |
| Hogs | −0.09 (0.27) |
17.1** (2.7) |
−0.032** (0.004) |
−4.9** (1.2) |
0.02 (0.03) |
| Oats | −0.54 (0.31) |
9.6** (2.1) |
−0.035** (0.005) |
0.18 (0.21) |
0.03 (0.03) |
| Oil | −5.0 (3.6) |
20.2** (3.7) |
−0.15** (0.01) |
18.0 (12.0) |
−0.02 (0.19) |
| Platinum | −1.9 (1.0) |
10.0 (5.8) |
0.081** (0.010) |
0.01 (0.19) |
0.15 (0.09) |
| Silver | −2.1** (0.3) |
4.6** (0.6) |
−0.043** (0.003) |
−0.89** (0.13) |
0.01 (0.02) |
| Soybeans | 1.54 (0.79) |
0.64 (2.15) |
−0.135 (0.009) |
−0.39 (0.34) |
0.07 (0.06) |
| Wheat | −0.69** (0.14) |
444** (0.64) |
−0.039** (0.003) |
−0.39 (0.20) |
0.03 (0.02) |
| Notes: Annual data. ** (*) means significantly different from zero at 0.01 (0.05) level. Standard errors in parentheses. Intercept and linear time trend included, not reported. VEC estimation, commodity by commodity, one lag. | |||||
Footnotes
Jeffrey Frankel is Harpel Professor, Kennedy School of Government, Harvard University and Director of the NBER's International Finance and Macroeconomics Program. Andrew Rose is Rocca Professor, Economic Analysis and Policy, Haas School of Business, UC Berkeley, CEPR Research Fellow and NBER Research Associate. This is a substantial revision of a paper presented at a workshop on 16–17 June 2009 at Westfälishche Wilhelms University Münster, Münster, Germany. For research assistance we thank: Ellis Connolly, Marc Hinterschweiger, Imran Kahn and Frederico Meinberg. We thank Harry Bloch, Mike Dooley, Mardi Dungey, Renée Fry, Don Harding, Christopher Kent, Lutz Kilian, Mariano Kulish, Marco Lombardi, Philip Lowe, Warwick McKibbin, Simon Price, Tony Richards, Larry Schembri, Klaus Schmidt-Hebbel, Susan Thorp, Shaun Vahey, Ine Van Robays and RBA conference participants for suggestions and comments. The datasets, key output and a current version of this paper are available on Rose's website <http://faculty.haas.berkeley.edu/arose/>. [1]
Expectations of future oil prices on the part of typical speculators, if anything, initially lagged behind contemporaneous spot prices. Furthermore, speculators have often been ‘net short’ (sellers) of commodities rather than ‘long’ (buyers). In other words, they may have delayed or moderated the price increases, rather than initiating or adding to them. [2]
See Krugman (2008a, 2008b) and Wolf (2008). [3]
See Frankel (2008a, 2008b), for example. A variant of the argument blaming the 2008 spike on easy monetary policy is that the mediating variable is expected inflation per se, rather than the real interest rate (Calvo 2008). [4]
For example, Barsky and Kilian (2002, 2004). [5]
We are indebted to Larry Summers for this point. [6]
The King of Saudi Arabia said at this time that his country might as well leave the reserves in the ground for its grandchildren (‘Saudi King Says Keeping Some Oil Finds for Future’, Reuters, 13 April 2008). [7]
For example, IMF (2007, 2008a, 2008b). [8]
See among others, Kohn (2008) and Krugman (2008a, 2008b). [9]
For example, Frankel (1984) and Calvo (2008). [10]
See Frankel (1986, 2008a, 2008b), among others. [11]
Fama and French (1987) and Bopp and Lady (1991) emphasise storage costs. [12]
Working (1949) and Breeden (1980) are classic references on the roles of carrying costs and the risk premium, respectively, in commodity markets. Yang, Bessler and Leatham (2001) review the literature. [13]
As in the (even more extensive) tests of the analogous unbiasedness propositions in the contexts of forward foreign exchange markets and the term structure of interest rates, the null hypothesis is usually rejected. Appendix A to this paper briefly reviews this literature. [14]
For example, Kolb (1992). [15]
This is the view of Calvo (2008). [16]
Ye, Zyren and Shore (2002, 2005, 2006) emphasise the role of inventories in forecasting oil prices. Notice that, once we condition on the real interest rate (and convenience yield), inventories have a negative effect on commodity prices, rather than the positive relationship that has appeared in the arguments of Kohn (2008), Krugman (2008a, 2008b) and Wolf (2008). [17]
We are implicitly assuming that the long-run commodity price can be modelled by a constant or trend term. [18]
See, for example, the discussion of Figure 1.22 in IMF (2006, pp 57–58). [19]
In theory, when estimating Equation (9), if inventories are already in the equation, the spread does not need to be added separately. But any available measure of inventories is likely to be incomplete, which might provide a reason to include the spread separately as a measure of speculative demand. [20]
Also inventories could perhaps be considered predetermined in higher-frequency data, since it takes time to make big additions to, or subtractions from, inventories. But in this paper we use annual data. [21]
For example, Protopapadakis and Stoll (1983, 1986) and Phillips and Pippenger (2005). [22]
For example, Mundell (2002). [23]
An application of the Dornbusch (1976) overshooting model can give us the prediction that the real exchange rate is proportionate to the real interest differential. It thus turns out that the real commodity price in local currency can be determined by the US real interest rate (and other determinants of the real US price) together with the differential in real interest rates between the domestic country and the United States. Equations along these lines are estimated in Frankel (2008a, Table 7.3, pp 307–310) for real commodity price indices in eight floating exchange rate countries: Australia, Brazil, Canada, Chile, Mexico, New Zealand, Switzerland and the United Kingdom. In almost every case, both the US real interest rate and the local–US real interest differential are found to have significant negative effects on local real commodity prices, just as hypothesised. [24]
Frankel (2008a) finds stronger evidence, especially for the relationship of commodity price indices and real interest rates. [25]
Further details concerning the series, and the dataset itself, are available on Andrew Rose's website <http://faculty.haas.berkeley.edu/arose/>. [26]
Alternative measurements are possible; in the future, we hope to use the implicit forward-looking expected volatility that can be extracted from options prices. [27]
We use world inventories insofar as possible, but substitute US inventories when this is missing (specifically, in the cases of copper, live cattle and hogs, oats, platinum and silver). [28]
In the past, we have also used US GDP, G7 GDP and industrial production (for the United States as well as for advanced countries in aggregate); the latter has the advantage of being available monthly. [29]
When we substitute G7 real GDP, the three commodity prices that showed significant correlations – not reported here – were: corn, cotton and soybeans. We view global output as a better measure than G7 GDP or industrial production, because it is more comprehensive. [30]
The results were a bit better when the same tests were run in terms of first differences (on data through 2007, not here reported but available in Table 1b of Frankel and Rose 2009, p 17). Correlation of price changes with G7 GDP growth was always positive, though again significant only for corn, cotton and soybeans. Correlations with volatility, the spread and inventories each show up as significant in five or six commodities out of eleven (and with the expected sign). [31]
We exclude the political risk measure. It gives generally unclear results, perhaps in part because its coverage is incomplete and/or because of the possible theoretical ambiguity mentioned earlier. Volatility seems to be better at capturing risk. A useful extension would be to use implicit volatility from options prices, which might combine the virtues of both the volatility and political risk variables. [32]
Unless otherwise noted, in our panel estimation we always include a common trend and commodity-specific intercepts; we do not report these coefficients. [33]
For example, Calvo (2008). [34]
Adding either a bandwagon or inflationary effect improves the fit of our equation: the within-commodity R2 rises from 0.58 to 0.66 in both cases. Fitted values for both perturbations are graphed against actual prices in the bottom panels of Figure 9. [35]
Studies of the time-series properties of real commodity prices can find a negative trend, positive trend, random walk, or mean reversion, depending on the sample period available when the authors do their study. Examples include Cuddington and Urzúa (1989) and Reinhart and Wickham (1994). [36]
We are implicitly considering inventories relative to full capacity, but explicit adjustment would improve the measurement, if the appropriate data on storage capacity could be found. [37]
See Yang et al (2001) for a review of the literature. [38]
References
Barsky RB and L Kilian (2002), ‘Do We Really Know that Oil Caused the Great Stagflation? A Monetary Alternative’, in BS Bernanke and KS Rogoff (eds), NBER Macroeconomics Annual 2001, 16, MIT Press, Cambridge, pp 137–183.
Barsky RB and L Kilian (2004), ‘Oil and the Macroeconomy since the 1970s’, Journal of Economic Perspectives, 18(4), pp 115–134.
Bessembinder H (1993), ‘An Empirical Analysis of Risk Premia in Futures Markets’, Journal of Futures Markets, 13(6), pp 611–630.
Bopp AE and GM Lady (1991), ‘A Comparison of Petroleum Futures versus Spot Prices as Predictors of Prices in the Future’, Energy Economics, 13(4), pp 274–282.
Breeden DT (1980), ‘Consumption Risks in Futures Markets’, Journal of Finance, 35(2), pp 503–520.
Brennan MJ (1958), ‘The Supply of Storage’, American Economic Review, 48(1), pp 50–72.
Brenner RJ and KF Kroner (1995), ‘Arbitrage, Cointegration, and Testing Unbiasedness Hypothesis in Financial Markets’, Journal of Financial and Quantitative Analysis, 30(1), pp 23–42.
Calvo G (2008), ‘Exploding Commodity Prices, Lax Monetary Policy, and Sovereign Wealth Funds’, Vox, 20 June. Available at <http://www.voxeu.org/index.php?q=node/1244#fn5>.
Carter CA (1999), ‘Commodity Futures Markets: A Survey’, Australian Journal of Agricultural and Resource Economics, 43(2), pp 209–247.
Chernenko SV, KB Schwarz and JH Wright (2004), ‘The Information Content of Forward and Futures Prices: Market Expectations and the Price of Risk’, Board of Governors of the Federal Reserve System International Finance Discussion Paper No 808.
Chinn MD, M LeBlanc and O Coibion (2005), ‘The Predictive Content of Energy Futures: An Update on Petroleum, Natural Gas, Heating Oil and Gasoline’, NBER Working Paper No 11033.
Choe B-J (1990), ‘Rational Expectations and Commodity Price Forecasts’, World Bank Policy, Research, and External Affairs Working Paper No 435.
Covey T and DA Bessler (1995), ‘Asset Storability and the Informational Content of Inter-Temporal Prices’, Journal of Empirical Finance, 2(2), pp 103–115.
Cuddington JT and CM Urzúa (1989), ‘Trends and Cycles in the Net Barter Terms of Trade: A New Approach’, Economic Journal, 99(396), pp 426–442.
Dornbusch R (1976), ‘Expectations and Exchange Rate Dynamics’, Journal of Political Economy, 84(6), pp 1161–1176.
Dusak K (1973), ‘Futures Trading and Investor Returns: An Investigation of Commodity Market Risk Premiums’, Journal of Political Economy, 81(6), pp 1387–1406.
Fama EF and KR French (1987), ‘Commodity Futures Prices: Some Evidence on Forecast Power, Premiums, and the Theory of Storage’, Journal of Business, 60(1), pp 55–73.
Fortenbery TR and HO Zapata (1998), ‘An Evaluation of Price Linkages between Futures and Cash Markets for Cheddar Cheese’, Journal of Futures Markets, 17(3), pp 279–301.
Frankel JA (1984), ‘Commodity Prices and Money: Lessons from International Finance’, American Journal of Agricultural Economics, 66(5), pp 560–566.
Frankel JA (1986), ‘Expectations and Commodity Price Dynamics: The Overshooting Model’, American Journal of Agricultural Economics, 68(2), pp 344–348.
Frankel JA (2008a), ‘The Effect of Monetary Policy on Real Commodity Prices’, in JY Campbell (ed), Asset Prices and Monetary Policy, University of Chicago Press, Chicago, pp 291–327.
Frankel JA (2008b), ‘An Explanation for Soaring Commodity Prices’, Vox, 25 March. Available at <http://www.voxeu.org/index.php?q=node/1002>.
Frankel JA and GA Hardouvelis (1985), ‘Commodity Prices, Money Surprises, and Fed Credibility’, Journal of Money, Credit and Banking, 17(4, Part I), pp 427–438.
Frankel JA and AK Rose (2009), ‘Macroeconomic Determination of Agricultural and Mineral Commodity Prices’, paper presented at the workshop ‘Challenges to Inflation in an Era of Relative Price Shocks’, Westfälishche Wilhelms University Münster, Münster, 16–17 June.
Froot KA and JA Frankel (1989), ‘Forward Discount Bias: Is It an Exchange Risk Premium?’, The Quarterly Journal of Economics, 104(1), pp 139–161.
Gorton GB, F Hayashi and KG Rouwenhorst (2007), ‘The Fundamentals of Commodity Futures Returns’, NBER Working Paper No 13249.
Gorton GB and KG Rouwenhorst (2006), ‘Facts and Fantasies about Commodity Futures’, Financial Analysts Journal, 62(2), pp 47–68.
Green SL and KA Mork (1991), ‘Toward Efficiency in the Crude-Oil Market’, Journal of Applied Econometrics, 6(1), pp 45–66.
Hazuka TB (1984), ‘Consumption Betas and Backwardation in Commodity Markets’, Journal of Finance, 39(3), pp 647–655.
IMF (International Monetary Fund) (2006), World Economic Outlook – Globalization and Inflation, World Economic and Financial Surveys, IMF, Washington DC.
IMF (2007), World Economic Outlook – Globalization and Inequality, World Economic and Financial Surveys, IMF, Washington DC.
IMF (2008a), World Economic Outlook – Financial Stress, Downturns, and Recoveries, World Economic and Financial Surveys, IMF, Washington DC.
IMF (2008b), World Economic Outlook – Housing and the Business Cycle, World Economic and Financial Surveys, IMF, Washington DC.
Kohn D (2008), ‘The Economic Outlook’, speech at the National Conference on ‘Public Employee Retirement Systems Annual Conference’, New Orleans, 20 May.
Kolb RW (1992), ‘Is Normal Backwardation Normal?’, Journal of Futures Markets, 12(1), pp 75–91.
Krugman P (2008a), ‘Commodity Prices (Wonkish)’, The New York Times, 19 March. Available at <http://krugman.blogs.nytimes.com/2008/03/19/commodity-prices-wonkish/>.
Krugman P (2008b), ‘The Oil Nonbubble’, The New York Times, 12 May. Available at <http://www.nytimes.com/2008/05/12/opinion/12krugman.html>.
Moosa IA and NE Al-Loughani (1994), ‘Unbiasedness and Time Varying Risk Premia in the Crude Oil Futures Market’, Energy Economics, 16(2), pp 99–105.
Morana C (2001), ‘A Semiparametric Approach to Short-Term Oil Price Forecasting’, Energy Economics, 23(3), pp 325–338.
Mundell R (2002), ‘Commodity Prices, Exchange Rates and the International Monetary System’, in Food and Agriculture Organization of the United Nations (FAO) (ed), Consultation on Agricultural Commodity Price Problems, FAO, Rome, pp 21–26.
Phillips L and JE Pippenger (2005), ‘Some Pitfalls in Testing the Law of One Price in Commodity Markets’, University of California, Santa Barbara, Economics Working Paper No WP 4-05.
Protopapadakis A and HR Stoll (1983), ‘Spot and Futures Prices and the Law of One Price’, Journal of Finance, 38(5), pp 1431–1455.
Protopapadakis A and HR Stoll (1986), ‘The Law of One Price in International Commodity Markets: A Reformulation and Some Formal Tests’, Journal of International Money and Finance, 5(3), pp 335–360.
Reinhart C and P Wickham (1994), ‘Commodity Prices: Cyclical Weakness or Secular Decline?’, IMF Staff Papers, 41(2), pp 175–213.
Tomek WG (1997), ‘Commodity Futures Prices as Forecasts’, Review of Agricultural Economics, 19(1), pp 23–44.
Wolf M (2008), ‘The Market Sets High Oil Prices to Tell Us What to Do’, Financial Times, Asian edn, 14 May, p 11.
Working H (1949), ‘The Theory of Price of Storage’, American Economic Review, 39(6), pp 1254–1262.
Yang J, DA Bessler and DJ Leatham (2001), ‘Asset Storability and Price Discovery in Commodity Futures Markets: A New Look’, Journal of Futures Markets, 21(3), pp 279–300.
Ye M, J Zyren and J Shore (2002), ‘Forecasting Crude Oil Spot Price Using OECD Petroleum Inventory Levels’, International Advances in Economic Research, 8(4), pp 324–334.
Ye M, J Zyren and J Shore (2005), ‘A Monthly Crude Oil Spot Price Forecasting Model Using Relative Inventories’, International Journal of Forecasting, 21(3), pp 491–501.
Ye M, J Zyren and J Shore (2006), ‘Forecasting Short-Run Crude Oil Price Using High- and Low-Inventory Variables’, Energy Policy, 34(17), pp 2736–2743.