RBA Annual Conference – 2009 Discussion
1. Simon Price
It is a pleasure to be invited to discuss this rich paper by Jeffrey Frankel and Andrew Rose. After the events of the past few years, with a range of commodity prices exhibiting great volatility, it is not hard to motivate Frankel and Rose's choice of topic, seen from either a long- or medium-term perspective. The authors use annual data, mainly in a panel context, to examine the relationship between real commodity prices and a number of macro and microeconomic series. What they are trying to do, I believe, is to adopt an eclectic approach that combines a classic model of short-run dynamics (articulated in, for example, Frankel 1986) with other considerations that may affect both short- and medium-term movements. Meanwhile, the very long run is relegated to essentially un-modelled trends. The empirical analysis is conducted using a variety of methods that, it is argued, allow us to conclude that the results are relatively robust.
The results are certainly thoroughly explored. The aim of my remarks is to step to one side, so to speak, to consider other ways of thinking about the relationship between the long-run and short-run dynamics of commodity prices with the intention of encouraging some discussion. I hope the observations given may thereby complement the paper, where the long run is somewhat pushed into the background. My comments probably also reflect my intellectual upbringing by adopting a UK-based econometric approach. Unhappily, I am the first to admit that I do not have a fully articulated alternative to the authors' approach, but that is the privilege of a discussant.
I am old enough to remember that some of us became concerned about the environment and resources back in the 1970s, even before the first oil price shock. At the time, one view was that prices of commodities – the exhaustible ones anyway – would inevitably rise as they became increasingly scarce. Another view was that naïve Malthusian views, as embodied in the Club of Rome's approach, were absurdly ignorant of economics and history. These opposing views were neatly captured in the famous bet between Paul Ehrlich and Julian Simon. Simon argued that contrary to the views of Ehrlich, economic forces and technical progress would together ensure that commodity prices would not tend to rise in the long run, and proposed a bet based on the prices of raw materials. Ehrlich and two of his colleagues accepted the challenge (see Ehrlich 1981) on the basis of the change in the real price of a basket of five metals between 29 September 1980 and 29 September 1990.
Looking even further back, Hotelling (1931) argued that the rent due to owners of exhaustible resources would rise at the rate of interest. This essentially followed from an arbitrage condition, and would seem to imply that exhaustible commodity prices should rise inexorably.
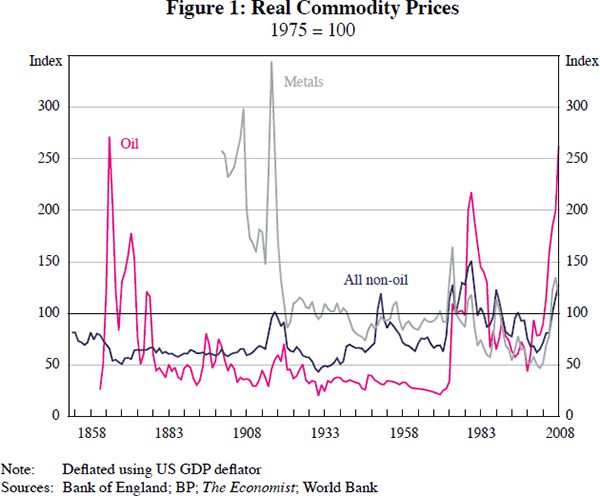
What happened? Simon won his bet, and as Figure 1 shows, the real price of oil (deflated by the US GDP deflator) in 2003 was lower than its average in the second half of the 19th century. Although the chart also shows that this was not true in 2008, it seems likely at the time of writing in August 2009 that the eventual outcome for 2009 will be below the 2008 figure. Metals prices are lower than when the series started in the late 19th century; while in the 20th century they appear to be mean reverting. Similarly, the series for all non-oil commodities shows no obvious trend. So the question is, is this in any sense a puzzle?
Hotelling's (1931) proposal was that the rent due to the owner of an exhaustible resource would rise at the rate of interest:

where: s is the spot price of the commodity; c is the marginal extraction cost; and i is the one-period nominal interest rate.
Equation (1) is an arbitrage condition as stated earlier. It applies under perfect competition. The question arises, why do the rents not get competed away? The answer is that the commodity is in fixed supply and no agent has an incentive to undercut.[1] But inspection of the data in Figure 1 does not suggest that exhaustible resources such as oil or metals rise at a rate determined solely by the real interest rate. The essential thing to grasp is that Equation (1) is a statement about the rent. So, in general, it is perfectly consistent with the data if ct has fallen.
What is missing here is some consideration of general equilibrium issues. That will determine the initial condition that is consistent with the behaviour of all agents, and will also provide dynamics even in a flexible-price model. Peter Sinclair has a nice paper, sadly as yet unpublished although available in preliminary form (Sinclair 2006), tying Hotelling into a macroeconomic model of optimal Ramsey growth with exhaustible resources. I will sketch his argument here. Clearly, from the Hotelling rule in general equilibrium (with perfect competition) the marginal product of oil, for example, must be rising at the rate of interest along the steady state path. So in equilibrium the real quantities (both for production and consumption) must be such that this holds. Sinclair discusses what determines the steady state.[2] The steady state here relates to variables that in this non-stochastic model are stationary: the interest rate; the proportional rate at which ‘oil’ is extracted; output growth; and the ratio of consumption to capital. Output, capital and the price of ‘oil’ all grow. It is the constellation of deep parameters such as the rate of time preference, the rate of technical progress and population growth that determine the steady state. Only a shock to such fundamental parameters will perturb the steady state path. But other shocks may have an influence on the short-term path.
Suppose that there is an unexpected discovery of ‘oil’. This would leave the steady state real interest rates and steady state rates of output growth and ‘oil’ extraction unaffected, although welfare would be higher and the paths for the levels of output and consumption would both jump. The ‘oil’ price would tumble on impact, and overshoot. It would jump to a point on the saddle path, along which the growth in the ‘oil’ price would differ from the long-run interest rate. Precise dynamics would depend on specific parametrisations. But my point is that there are real models that exhibit jumps in the ‘oil’ price and which may exhibit overshooting, but that overshoot need not be driven by sticky prices.
In the long run, what will determine the price of commodities? Although extraction costs are not in the formal model, a secular decline over time may well be a prime candidate for the long-run rise in prices to be less than implied by the interest rate. Higher impatience (the pure rate of time preference) will raise the real rate of interest so the spot price will jump down and the real oil price will rise faster in the long run. Eventually, the new level of prices will cross the previous path. Other deep parameters have other effects. As usual, it is hard to talk about the level of output or capital ‘affecting’ the price because they are endogenous; similarly, the rate of interest is endogenous. However, we might be able to say something about how output or interest rates co-move with ‘oil’ prices after a specific shock. If over time shocks tended to be of the same species, we would observe apparently stable, but essentially reduced-form, relationships between different endogenous and non-stationary variables (the real oil price and output, for example).
Taken literally, Hotelling suggests that the ‘oil’ price will be ‘integrated of order 1’ (I(1)) (unless the interest rate is a constant, in which case it will be trend stationary). Sinclair's (2006) Macro-Hotelling model also suggests that the ‘oil’ price will be I(1), and cointegrated or co-breaking with fundamental drivers. But those drivers are hard to measure. In a similar vein, Pindyck (1999) argues from a partial equilibrium perspective that such prices should revert to unobservable stochastic trends. However, from the co-movements of endogenous variables, we might observe cointegration with output, or indeed the long-run interest rate. Nevertheless, we should be aware this does not imply a structural relationship. This is a point that Lutz Killian has made repeatedly in a different way in his analysis of oil prices using structural decompositions, as is made clear, for example, in the title of Kilian (2009) ‘Not All Oil Price Shocks Are Alike’.
Still on the subject of univariate time series properties, in an interesting paper, Lee, List and Strazicich (2005) look at the real prices of 11 natural resources from 1870 to 1990. They have a unit root test which allows for endogenously determined structural breaks with and without a quadratic trend. Contrary to some earlier research cited in their paper (for example, Berck and Roberts 1996), they find evidence against the unit root hypothesis for all price series. Natural resource prices are stationary around deterministic trends with structural breaks. So this is not strictly consistent with Hotelling unless the real interest rate is non-stochastic. But the message to take away is that breaks may matter.
It must be said that the commodities examined in Jeffrey and Andrew's paper are not exclusively exhaustible. Agricultural commodities are not usually thought of as such, although a read of Jared Diamond (2005, for example) provides plenty of examples where agricultural output has been (and often remains) unsustainable. Of course, there is an inventory arbitrage condition at work in any storable commodity, to which the authors appeal in their motivation.
So to return more specifically to the paper, in Frankel's formal model (Frankel
1986) we also have price jumps, where the mechanism is not capital accumulation
but sticky prices à la Dornbusch (1976). But in both cases we have
short-run dynamics that are converging on the long-run – 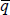 in terms of the paper. In the less formal model, we have a variety of mechanisms
at work. On interest rates, to quote the related paper Frankel (2006, p 5):
in terms of the paper. In the less formal model, we have a variety of mechanisms
at work. On interest rates, to quote the related paper Frankel (2006, p 5):
High interest rates reduce the demand for storable commodities, or increase the supply, through a variety of channels:
- by increasing the incentive for extraction today rather than tomorrow (think of the rates at which oil is pumped, gold mined, forests logged, or livestock herds culled)
- by decreasing firms' desire to carry inventories (think of oil inventories held in tanks)
- by encouraging speculators to shift out of commodity contracts (especially spot contracts), and into treasury bills.
So I suppose my question is, what are we looking at – short-run dynamics or long-run determinants? I think the answer is that the authors take an eclectic approach and try to tease out what the data tell us. In which case we might ask how best to do that.
I was raised in what is sometimes called the Oxford-Copenhagen view of time series analysis, which takes the distinction between stationary and non-stationary data very seriously. This, and my discussion above, pushes me towards an analysis where there is a long-run relationship between commodity prices and their fundamentals, perturbed by shocks, with equilibration towards the long run that does not have to take place exclusively via prices: that is, a vector error correction mechanism (VECM). And it is not obvious, given the differences between commodities, that either the long-run relationships or short-run dynamics are common between the commodities.
While the authors report some cointegration tests and present results in an appendix, it strikes me as worthwhile to think more about these issues, particularly because several of the series included in their VECMs appear to be stationary. I have already suggested that prices may follow stochastic trends, and that things that move the steady state around will be cointegrated with prices. So one might expect to find cointegration with those long-run drivers, if one could work out what they are. However, that is a difficult task. I have also argued that we might observe a (non-structural) relationship between the level of output and the oil price. If technical progress were deterministic, we might also observe a linear trend, which is mainly what the authors use in their regressions. So these might be specifications worth exploring, with the stationary ‘micro’ series relegated to the dynamics. A lack of data might make this difficult, however, as the annual series mean that the number of data points is small.
One prominently exploited aspect of the paper is that the data constitute a panel. While I have argued that, in principle, long-run shocks are unlikely to be identical across the series, it may be true that there remains considerable co-movement in the price series. I took quarterly series of the real prices of cattle, copper, corn, hogs, soybeans, wheat and oil that I had to hand from 1977:Q1 to 2009:Q2. Two principal components explain 83 per cent of the variation of this data in levels terms. Similarly, in Jeffrey and Andrew's annual data set, two principal components explain 81.5 per cent (53.3 per cent) of the variance of the price levels (inflation rates). These are high proportions that by themselves support pooling, but inspection of the loadings on the two factors show that they vary markedly between series, indicating heterogeneity. So despite the common variance, this suggests that pooling the data will not necessarily be helpful. Another way to look at this is to simply compare the time series of the price series as shown in Figure 2 (these are normalised to unity at the start of the sample). I have not labelled the series, as the point of this exercise is to highlight the diversity in the data. The figure suggests to me that at least the long-run drivers do differ. Perhaps the panel approach is most helpful for assessing the short-run covariances and dynamics.
One way of modelling this short-run dependence might be to estimate a seemingly unrelated regression (SUR) on individual error correction mechanism (ECM) relationships. Pesaran, Shin and Smith (1999) suggest a related pooled mean group (PMG) approach. They argue that in dynamic panels there may be common long-run effects that may increase efficiency of estimation if they are exploited. I suspect those common effects are implausible in this case, but given we have a small system here we might be able to feasibly estimate a SUR without imposing long-run homogeneity, although higher-frequency data would probably be necessary. Alternatively, if the aim is to estimate the average long-run effects of the variables in the system, then the PMG method may be efficient even in the absence of homogeneity in the parameters; there is a Hausman test for this.
To conclude, both the authors' and a possible general equilibrium Ramsey growth theory suggest that there are long-run relations and short-run dynamics to model. Unfortunately, this may not best be captured in an essentially static framework. Exhaustible and agricultural products are likely to be driven very differently, again suggesting that pooling may not be the obvious approach to adopt. A VECM or system ECM approach might shed some different light on what drives commodity prices. Or perhaps an attempt to identify shocks, as in Lutz Killian's work, might be productive.
References
Berck P and M Roberts (1996), ‘Natural Resource Prices: Will They Ever Turn Up?’, Journal of Environmental Economics and Management, 31(1), pp 65–78.
Diamond JM (2005), Collapse: How Societies Choose to Fail or Survive, Allen Lane Science, London.
Dornbusch R (1976), ‘Expectations and Exchange Rate Dynamics’, Journal of Political Economy, 84(6), pp 1161–1176.
Ehrlich PR (1981), ‘An Economist in Wonderland’, Social Science Quarterly, 62, pp 44–19.
Frankel JA (1986), ‘Expectations and Commodity Price Dynamics: The Overshooting Model’, American Journal of Agricultural Economics, 68(2), pp 344–348.
Frankel JA (2006), ‘The Effect of Monetary Policy on Real Commodity Prices’, NBER Working Paper No 12713.
Hotelling H (1931), ‘The Economics of Exhaustible Resources’, The Journal of Political Economy, 39(2), pp 137–175.
Kilian L (2009), ‘Not All Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market’, American Economic Review, 99(3), pp 1053–1069.
Lee J, JA List and MC Strazicich (2005), ‘Nonrenewable Resource Prices: Deterministic or Stochastic Trends?’, NBER Working Paper No 11487.
Pesaran MH, Y Shin and RP Smith (1999), ‘Pooled Mean Group Estimation of Dynamic Heterogeneous Panels’, Journal of the American Statistical Association, 94(446), pp 621–634.
Pindyck RS (1999), ‘The Long-Run Evolution of Energy Prices’, The Energy Journal, 20(2), pp 1–27.
Sinclair PJN (1994), ‘On the Optimum Trend of Fossil Fuel Taxation’, Oxford Economic Papers, 46, Special Issue on Environmental Economics, pp 869–877.
Sinclair PJN (2006), ‘A Simple Guide to the Basic Macroeconomics of Oil’, Centre for Dynamic Macroeconomic Analysis Conference Paper No 06/08. Available at <http://www.st-andrews.ac.uk/economics/CDMA/papers/cp0608.pdf>.
2. General Discussion
Much of the discussion surrounding Jeffrey Frankel and Andrew Rose's paper focused on the results related to the macroeconomic rather than the microeconomic determinants of commodity prices. A number of participants were concerned that measures of world economic activity did not have a more significant role in explaining commodity prices given their prior beliefs. Some participants wondered whether this was due to problems with constructing a measure of global activity relevant to commodity prices. One participant commented that world GDP was not the best measure of world output and that using other measures of industrial output may yield different results. Another suggested that the authors should experiment with some of the measures used by Lutz Kilian, or Ine Van Robay's measure of industrial production, which includes China. Andrew Rose responded by noting that their paper reports results based on a wide range of measures of global output, but that the findings were consistent across all of these. He thought that it might be worth trying some of the industrial production measures that had been suggested, but if they produced a different outcome to those of the other measures of output they had already examined, the overall conclusion would have to be that the results for global activity are not very robust. Other participants wondered whether some of the effects of stronger economic activity over recent years had been captured instead by the measure of inventories.
In response to Simon Price's questions about what drives the long-run evolution of commodity prices and how the long-run dynamics might be estimated, Andrew Rose suggested that the 48-year span of the dataset was insufficient for estimating the long-run relationship between commodity prices and macroeconomic factors, particularly given that the data were annual.
The discussion also touched on issues surrounding the nature of the supply side of commodity markets. In particular, given considerable differences in the elasticities of supply across commodities and differences in the long-term evolution of the prices of the commodities examined, there was some scepticism regarding the value of the paper's results based on pooled regressions. Andrew Rose emphasised that that is why they also had looked at unpooled results in the robustness checks, which were consistent with the pooled results. He again emphasised that much of the variation of the commodity prices over time could be accounted for by microeconomic factors. Even so, a participant suggested that more could be done to better understand the role of supply-side factors in determining commodity prices. In this regard, reference was made to previous episodes of significant commodity price movements where supply-side factors appeared to have played an important role, such as the oil price movements of the 1970s. Similarly, it was argued that the more recent run-up in commodity prices was partly a function of tight supply due to the lack of global exploration for commodities in the 1990s. Andrew Rose sympathised with the comments, but pointed to constraints on available data which precluded the use of supply-related variables.
Finally, the discussion turned to what the results, considered together with the framework of the paper, might imply for the level of commodity prices. There was particular interest in the question of whether commodity prices are indeed sustainable at the higher levels of late. Andrew Rose noted that their results had little to say on this question, but that it was an interesting area for future research. One participant noted that the rise of commodity prices over recent years had reversed a long downward trend associated with considerable productivity growth in the resources sector, and wondered if such trends will reassert themselves in time.