RBA Annual Conference – 2009 Discussion
1. Mardi Dungey
This paper is one in a set of related papers recently put forward by Gert Peersman, in conjunction with the co-authors of this paper, Christiane Baumeister and Ine Van Robays. This body of work commendably attempts to more thoroughly explore the empirical linkages between oil price fluctuations and real economic outcomes for a variety of countries, in the hope of drawing together some general results about the impact of shocks to oil prices on the economy. Such generalisations are undoubtedly important for policy-makers. If it is possible to assess the expected response of an economy to a shock to oil prices based on the structure of the economy, then it will become somewhat easier to advocate appropriate policy responses.
What do we know?
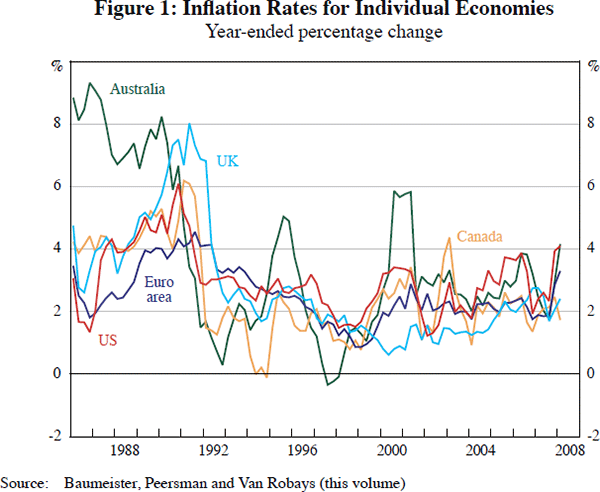
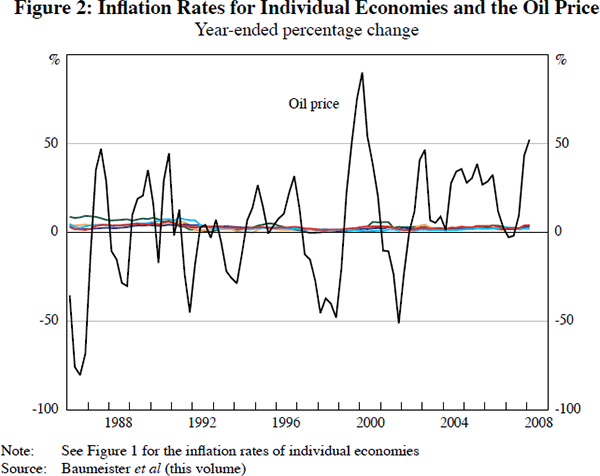
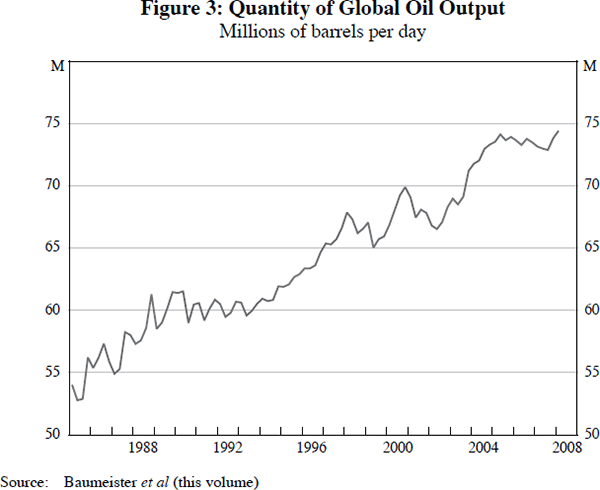
There is plenty of evidence that inflation behaviour in many countries is quite similar; see for example Figure 1, which compares the inflation rates for the economies in Christiane, Gert and Ine's sample. The figure shows the clear commonality in inflation rates, and there is a literature concerned with capturing the effects of global influences on inflation in individual countries, (for example, Binyamini and Razin 2008). The issue has also come to be associated with vector autoregression (VAR) estimates of individual country models as far back as Sims (1992), where he proposed that the price puzzle evident in many small VARs could be explained by capturing some measure of inflationary expectations, for which either commodity prices or oil prices could be useful proxies (an Australian example is provided by Brischetto and Voss 1999). Rather, Christiane, Gert and Ine attempt to use VAR estimates to distinguish the impact of oil market developments on economies. It is apparent that this link will be non-trivial to model by a simple comparison of the inflation rates of interest with changes in oil prices, shown in Figure 2. The volatility in oil prices swamps that in inflation rates, making its role as a proxy for a common factor unlikely. Christiane, Gert and Ine implicitly acknowledge this by attempting to disentangle the demand and supply shocks – if we examine the output profile of oil, through their quantity measure shown in Figure 3, it is apparent that this is also a relatively volatile series. As Christiane, Gert and Ine are at pains to point out, changes in oil output relate to both supply- and demand-side shocks, requiring appropriate identification technology.
Data selection
It is relatively well known that data intensive estimation methods such as VARs are sensitive to data choices. It then behoves me to make a number of comments on the selection of data for this paper, and the problems which may occur with cross-country comparisons. The first problem is that not all data sources are created equal. As we are all aware, the euro area did not exist prior to the official adoption of the euro in 1999, although some euro area data exist from the early 1990s courtesy of Eurostat. Even these data, however, are tainted by changing definitions of the countries in the euro area. The data used to represent the euro area in this paper are drawn from the Area-Wide Model (AWM) database of Fagan, Henry and Mestre (2001), a database conveniently available from the Euro Area Business Cycle Network (EABCN) for download. Euro area aggregates in this database are based on country data which are aggregated using PPP GDP-fixed weights for the entire pre-official euro area data. The weights are fixed in 2001. The back data for the euro area consumer price index are constructed using an entirely different set of weights based on household survey data, with back data constructed based on 1995 weights (see Anderson et al 2007 for a discussion). This may not be such a problem for the real data, but is a significant one for the financial data, particularly interest rates. Ehrmann and Fratzscher (2005) in fact find a significant break in the financial data at precisely the point at which this splicing would occur. The lack of real euro area data is likely to cause significant problems with sensitivity of the estimation, and the question of which data should be used is a lively area of debate with Brüggemann and Lütkepohl (2006) preferring German data, Beyer, Doornick and Hendry (2001) advocating nominal growth rate splicing and Anderson et al (2007) proposing sliding weights for financial market data based on distance from a measure of centrality in order to play down the effects of Italian and Portuguese financial markets. These issues should at least rate a mention in the paper – the AWM database was not designed to be a catch-all database for all applications.
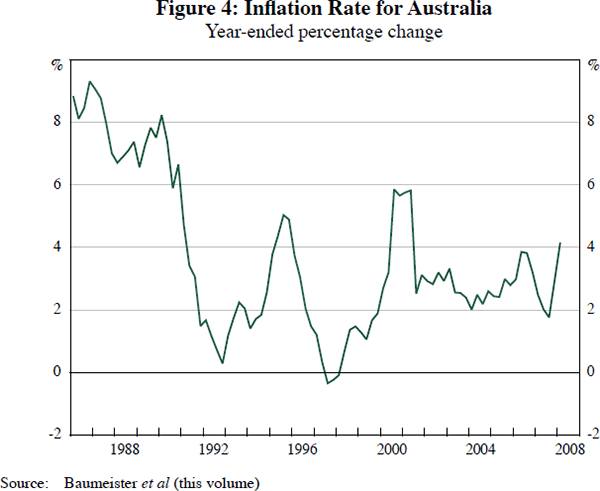
The second problem is appropriate recognition of structural breaks and outliers in the data. A good example in the current context is the Australian CPI data. This is shown below in Figure 4. The impact of the introduction of the goods and services tax in 2000 is clearly evident as a short-lived increase in the inflation rate. Without controls for special features of the data such as this, significant distortions may arise. For example, using Christiane, Gert and Ine's data I estimated a very simple version of a linear Taylor rule for Australia with and without a dummy variable for the GST. The weights on inflation for these specifications are given in Table 1. Clearly, the dummy is significant, and its exclusion suggests that the Reserve Bank of Australia places a lower weight on domestic inflationary pressures than is the case when the appropriate control is in place.
| No dummy for GST | With dummy for GST | |
|---|---|---|
| Coefficient on inflation | 0.18 (0.05) |
0.25 (0.07) |
| Coefficient on dummy | na | −1.02 (0.46) |
| Notes: With interest rate smoothing. Standard errors in parentheses. | ||
Estimation methodology
This paper makes clever use of the sign restriction methodology to identify oil price shocks. By examining combinations of quantity and price responses to shocks in a VAR framework, the authors impose an identification which effectively supports demand from supply. This is very powerful. However, we need to be careful with this technology. Here three types of shocks are identified. One, when prices and quantities move in the same direction (a demand shock), a second when prices and quantities move in the opposite direction (a supply shock) and a third when prices and quantities move in the same direction but world output moves in the opposite direction (an oil-specific demand shock). These restrictions are imposed for four quarters. Although four quarters has become common in the literature, there is as yet no real methodology for determining the appropriate length of time which ‘should’ be applied. One of the criteria seems to be of reasonableness – and that we wish to find a sufficient number of identified draws in simulation. In this case, when the system is simulated the sign restrictions are satisfied some 25 per cent of the time – in effect this means that 75 per cent of the rotated draws are not satisfactory combinations. Again, we have no criteria to judge whether this is reasonable or not.
Peersman (2005) was one of the earlier papers to implement sign restrictions. Fry and Pagan (2007) show that the choice of point estimates for the sign-restricted impulse responses in that paper does not preserve the orthogonality of the shocks represented in the impulses. Without orthogonality, not only are the impulse response functions inconsistently generated but variance decompositions, such as given in Peersman, will be invalid. Simply, the Peersman proposal chose the median realisation of the acceptable simulated impulses at each point of time in the forecast horizon, which does not guarantee orthogonality. Fry and Pagan propose a simple distance estimator to overcome this problem in selecting the point estimate, and show that it can make a considerable difference to the impulse response function. In the current paper, it is not clear that such a correction has been applied to ensure the orthogonality of shocks at all points. If not, this should be undertaken to confirm the validity of the results.
Cross-country evidence
The novelty of this paper is the application of the identification methodology to a relatively wide range of economies, representing net oil importers and exporters, net importers and exporters of other energy sources, and large and small open economies. A potential problem is whether the shocks identified in each of the individual models for oil demand and supply are equivalent across the economies, validating the cross-country comparisons.
The authors present their model results for separate country groups defined according to these different economic structures. The first are energy importers, which import both oil and other energy substitutes: Japan, the euro area and Switzerland fall clearly into this category. The second are net oil importers, which largely import oil but export other energy substitutes: the United States, Australia and Canada are primary examples. The third are net oil exporters, which export oil but import other energy substitutes, such as the United Kingdom. And finally, there are oil-exporting countries who do not rely on other energy substitutes, such as Norway.
Overlaid on this distinction based on trade in energy, there are important differences in terms of the size and openness of the economies. Australia, Canada and Norway are all small open commodity-exporting economies. Japan and the euro area are typically classified as larger open economies, with the United Kingdom somewhere between these and the commodity exporters. Typically the United States is represented as a large closed economy.
The conclusions drawn by Christiane, Gert and Ine based on their categorisation of energy importers, and two categories of net energy importers and energy exporters, can be summarised as follows. An adverse oil supply shock results in permanently lower output for energy importers of all kinds, but is insignificant or occasionally positive for energy exporters. Inflationary effects may be offset by exchange rate movements, but are not always. Oil demand shocks are less able to be divided by the energy status of the individual economies.
Consider now whether the openness of the economies can also be related to the results. Small open economies seem to have smaller (and largely insignificant) impacts from an oil supply shock and their inflationary responses are also muted and insignificant. The shock does result in significant interest rate response in Australia, the euro area, the United Kingdom and Switzerland. Only in Japan, Canada and the United Kingdom are the output responses to oil demand shocks (from either source) significantly different from zero at a longer horizon. All countries experience significant inflation increases from an economic activity-driven oil demand shock. On the other hand, only the United Kingdom (and possibly the United States, it is not clear from the figure) have a significant inflationary impact from an oil-specific demand shock. In fact, it seems that it is difficult to make any generalisations regarding the effects of oil demand shocks based on either the classification of the energy import/export status or their openness.
Time-varying evidence
The authors present evidence drawn from a previous paper that the elasticity of demand for oil has changed within the sample period. Consequently, they re-estimate the VAR models and examine whether there are differences in impulses between the two sample periods. In general, they conclude that the responses in the later (1990s) period are muted compared with the earlier (1970s) period. This tallies with our understanding of economic relationships over the period. I would like to suggest that the authors consider an alternative representation of their results. By estimating the early period SVAR and projecting it forward into the later period, they can examine the different outcomes the early model predicts when encountering the later period shocks, and clearly examine the differences between them. This is in the spirit of the projections given in Dungey, Fry and Martin (2004). Another useful extension would be to decompose individual country inflation data into its components using an historical decomposition, where each component depends on the contribution of all previous shocks of a particular type – that is, the value of any variable in the VAR can be represented as a weighted sum of all previous shocks. This is a reorganisation of the information in the impulse responses, somewhat different to a forecast error variance decomposition, but it can be useful in obtaining a view of the relative importance of different shocks to domestic inflation over the period of interest. In this way it would be possible to say something about the relative importance of oil supply, oil demand and domestic shocks to the evolution of domestic inflation. With information about the sources of shocks it will be easier to assess the performance of monetary policy in response.
Concluding remarks
In summary, this paper is a contribution to better understanding of the effects of oil price shocks on economies, in light of the differences in the structure of the individual economies.
The identification of the oil price shocks in the paper is intelligent, but this is not the novelty of this paper. Rather, the authors concentrate on classifying the characteristics of economies in order to understand the way in which they respond to oil shocks. The paper is not quite in the vein of the global VAR (GVAR) papers of Dees et al (2007) and Dees et al (2009), but there are overlaps. In the GVAR, each country is treated as an individual module, where the structure of these modules is identical. The novelty of the GVAR modelling approach is that it uses a consistent means of interaction between countries, via a relationship with the rest of the world. In Christiane, Gert and Ine's paper we have a similar modular style of approach to the countries, with each linked to a rest-of-world activity variable, but we do not have interactions between all of the economies in a single model. It would be beneficial to take this one step further and take account of the structural idiosyncrasies of the data in these economies to further refine the results. Then we could be surer that the generalisations we desire are not being driven by outliers or anomalies, something which seems to be absolutely desirable from a policy-making perspective.
References
Anderson HM, M Dungey, DR Osborn and F Vahid (2007), ‘Constructing Historical Euro Area Data’, CAMA Working Paper No 18/2007.
Beyer A, JA Doornick and DF Hendry (2001), ‘Constructing Historical Euro-Zone Data’, The Economic Journal, 111(469), pp F102–F121.
Binyamini A and A Razin (2008), ‘Inflation-Output Tradeoff as Equilibrium Outcome of Globalization’, NBER Working Paper No 14379.
Brischetto A and G Voss (1999), ‘A Structural Vector Autoregression Model of Monetary Policy in Australia’, RBA Research Discussion Paper No 1999-11.
Brüggemann R and H Lütkepohl (2006), ‘A Small Monetary System for the Euro Area Based on German Data’, Journal of Applied Econometrics, 21(6), pp 683–702.
Dees S, P di Mauro, MH Pesaran and LV Smith (2007), ‘Exploring the International Linkages of the Euro Area: A Global VAR Analysis’, Journal of Applied Econometrics, 22(1), pp 1–38.
Dees S, MH Pesaran, LV Smith and RP Smith (2009), ‘Identification of New Keynesian Phillips Curves from a Global Perspective’, Journal of Money, Credit and Banking, 41(7), pp 1481–1502.
Dungey M, R Fry and VL Martin (2004), ‘Identification of Common and Idiosyncratic Shocks in Real Equity Prices: Australia 1982–2002’, Global Finance Journal, 15(1), pp 81–102.
Ehrmann M and M Fratzscher (2005), ‘Equal Size, Equal Role? Interest Rate Interdependence between the Euro Area and the United States’, The Economic Journal, 115(506), pp 928–948.
Fagan G, J Henry and R Mestre (2001) , ‘An Area-Wide Model (AWM) for the Euro Area’, ECB Working Paper No 42.
Fry R and A Pagan (2007), ‘Some Issues in Using Sign Restrictions for Identifying Structural VARs’, National Centre for Econometric Research Working Paper No 14.
Peersman G (2005), ‘What Caused the Early Millennium Slowdown? Evidence Based on Vector Autoregressions’, Journal of Applied Econometrics, 20(2), pp 185–207.
Sims CA (1992), ‘Interpreting the Macroeconomic Time Series Facts: The Effects of Monetary Policy’, European Economic Review, 36(5), pp 975–1000.
2. General Discussion
Three themes emerged from the discussion on the paper presented by Ine Van Robays examining the varying reactions to oil demand and oil supply shocks across economies, many following on from those raised in the first session of the conference.
There was some discussion of how best to measure real activity. A participant noted that the paper used a broad measure of output starting from 1986, but this came at the cost of a diminished sample length. This raised a concern that the parameter estimates of the VAR model may be compromised by the lack of sample data. Another participant expanded on this point by noting that not only was it difficult to accurately estimate the coefficients of the model given the number of variables and available observations, but that extending the sample further back in time would encompass larger shocks specific to the oil market, namely those of the 1970s. It was suggested that incorporating these would better identify the VAR model, particularly in terms of the key oil supply and demand shocks of the model.
The second theme was introduced by a participant who wondered whether the nature of the impulse responses to oil shocks depends on where along the supply curve the economy is to begin with. If so, it was suggested that this might have important implications for monetary policy; if the economy is on the inelastic part of the supply curve, the response of prices to a general demand shock would be larger than if the economy was on a flatter portion of the curve. A related line of discussion arose regarding possible movements in the oil supply curve, with one participant conjecturing that the oil supply curve was becoming steeper. Another participant followed this up by raising the question of the consequences of a significant expansion of demand shifting the world economy up the supply curve. In response, a participant thought that the suggestion of moving up the global supply curve is not as severe as perhaps implied by the results of the paper because the world would find ways to adjust to short- and even medium-run supply constraints. They went on to claim that, but for the financial crisis, there would have been a significant amount of capital available to expand the supply of oil. It was noted, however, that while a rightward shift in the oil supply curve may be likely, it could take a long time and in the meantime, monetary policy-makers needed to consider the implications of a movement up the oil supply curve.
There was some debate about the assumptions used in the VAR model of the paper in relation to the supply of oil. One participant suggested that the supply of oil is a function of the decisions taken by swing producers, and that the VAR approach does not adequately model these decisions which will have an important influence on prices over the longer run. Another participant responded to this comment by explaining that the VAR approach used in the paper does not restrict the long-run response, but rather identifies shocks by making assumptions about the short-run responses of the economy to different types of shocks.
The third theme of the discussion was the importance of second-round effects on the inflation and monetary policy responses. One participant appreciated the precision with which the paper defined the direct and second-round effects. Another highlighted the paper's results regarding differences across economies in the impulse responses to oil supply shocks and suggested that they were potentially explained by differences in labour market flexibility.