RDP 2013-10: Stochastic Terms of Trade Volatility in Small Open Economies 7. Robustness Checks
August 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 1.06MB
In this section we examine the robustness of our results to alternative parameter assumptions and modeling choices.
7.1 Alternative Parameter Values
As a first exercise, we test the sensitivity of our model's dynamics to alternative parameter values. In particular we consider: (i) increasing the inverse of the labour supply elasticity, ζ, from 2 to 100; (ii) increasing the inverse of the elasticity of substitution, σ, from 2 to 10; and (iii) increasing the parameter governing the sensitivity of the risk-free interest rate to the foreign debt level, ψ, from 10−3 to 10−2. We examine each of these alternative parameter choices separately, leaving the other parameters at the same level as in the baseline model presented above. Figures 9 and 10 show impulse responses to a one standard deviation terms of trade volatility shock in Australia under the alternative parameter values.
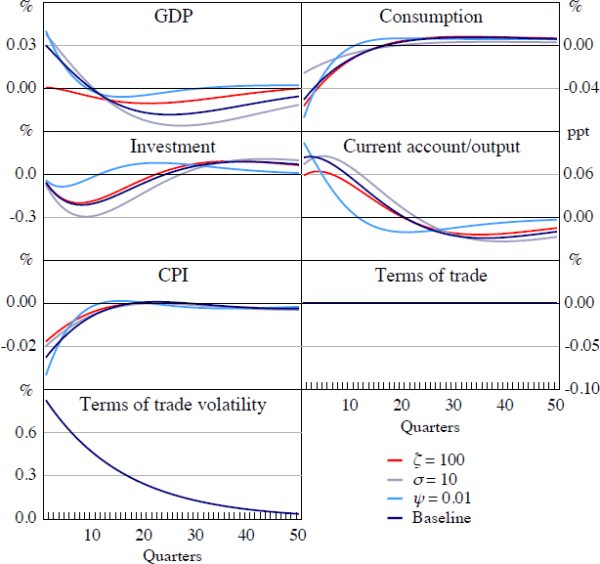
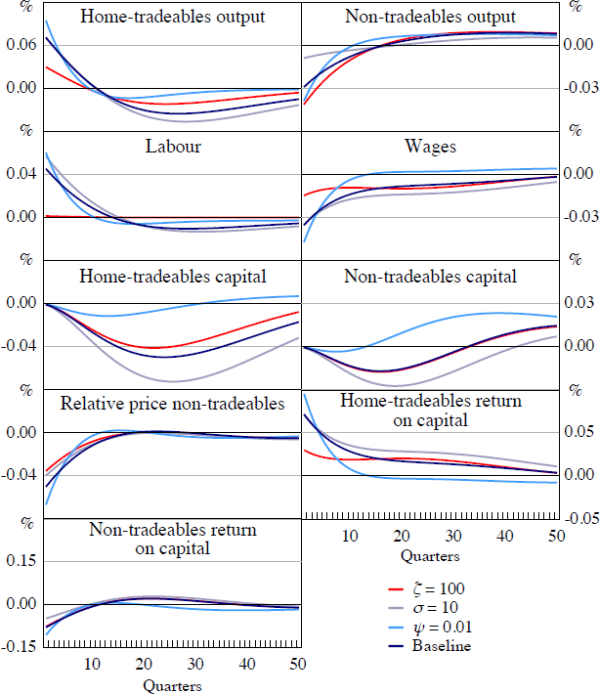
An increase in ζ decreases the willingness of households to adjust their labour supply in response to macroeconomic shocks. Relative to the baseline case, an increase in terms of trade volatility now triggers a smaller increase in tradeables output, larger contraction in non-tradeables output and consumption, and a larger improvement in the current account. That is, because households are less willing to respond to adverse income shocks by increasing their labour supply, they engage in more precautionary foreign asset accumulation. Aggregate GDP also decreases following the shock in this scenario, consistent with the empirical responses in Section 4.
In contrast, a decrease in the intertemporal elasticity of substitution (equivalent to an increase in σ) reduces the consumption response to changes in terms of trade volatility. This largely occurs through a smaller decline in non-tradeables consumption, leaving the response of the other variables largely unaffected.
In our baseline results, we assumed an extremely low value of ψ in order to minimise the effect of this parameter on the dynamics of the model. Other papers that have estimated the value of this parameter for various countries have tended to find higher values.[15] A higher value of ψ penalises the economy for varying its stock of foreign assets. Setting this parameter to 10−2 reduces the amount of time that it takes for the model to converge to its steady state. However, the initial responses of the variables to the terms of trade volatility shock are broadly similar to the baseline model.
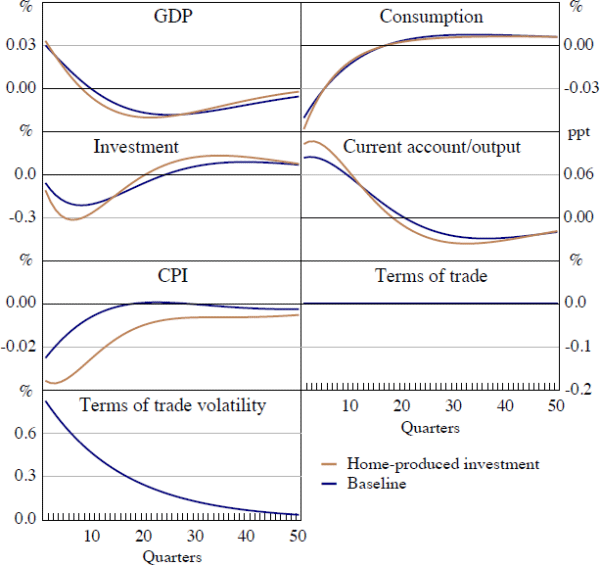
7.2 Home-produced Components of Investment
In our baseline model we assumed that the investment good was priced in units of the foreign tradeable good. This choice was motivated by the stylised fact that prices of investment goods differ less across countries than the prices of consumption goods (Hsieh and Klenow 2009). In this exercise, we instead assume that the investment good is priced in the same units as the economy's consumption good. That is, we allow the prices of home-produced goods to affect prices of investment goods. To do this, we assume that the investment good is a constant elasticity of substitution aggregate of tradeable and non-tradeable goods and that the tradeable component is itself an aggregate of home and foreign tradeable goods.[16]
Because we are interested in how including home-produced investment goods affects the fit of the model, as well as the dynamics, we first recalibrate the new model to match the same moments of the data as we did with the baseline model. Table 8 shows the resulting model moments for Australia. Including a home-produced component of investment goods increases the correlation between investment and output marginally, which improves the fit of the model in that dimension. However, it also reduces the volatility of consumption relative to that of output.
| σy | σc/σy | σi/σy | ρc,y | ρi,y | ρnx,y | nx/y | |
|---|---|---|---|---|---|---|---|
| Data | 1.35 | 0.81 | 2.97 | 0.49 | 0.67 | −0.22 | −0.94 |
| Model | 1.36 | 0.46 | 2.97 | 0.56 | 0.28 | 0.55 | −0.94 |
Next, we examine the dynamic response of the economy to a terms of trade volatility shock, shown in Figure 11. Including a home-produced component of investment has very little effect on the response of the economy to a volatility shock. In sum, in terms of both model fit and dynamics there seems to be little to choose between the two model specifications.
Footnotes
For example, Fernández-Villaverde et al (2011) for a selection of South American economies and Jaaskela and Nimark (2011) for Australia, while Justiniano and Preston (2010) calibrated this parameter to 10−2 in models of Australia, Canada and New Zealand. [15]
To be precise:
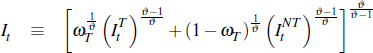 and
and
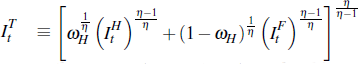 , where ωT
is the share of tradeable goods in the aggregate investment good, while ωH
is the share of the home-produced goods in the tradeables goods aggregate.
[16]
, where ωT
is the share of tradeable goods in the aggregate investment good, while ωH
is the share of the home-produced goods in the tradeables goods aggregate.
[16]