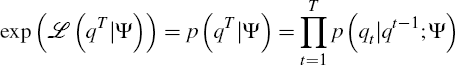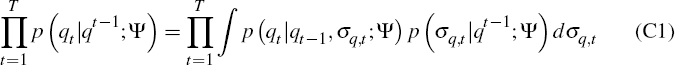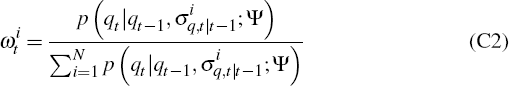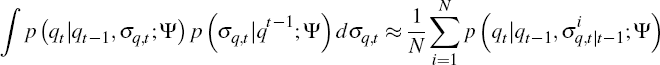RDP 2013-10: Stochastic Terms of Trade Volatility in Small Open Economies Appendix C: Estimating Stochastic Volatility

This appendix describes our procedure for estimating the stochastic volatility of the terms of trade. For a more detailed description of the use of the particle filter to estimate macroeconomic models, see Fernández-Villaverde and Rubio-Ramírez (2007).

Denote the vector of parameters to be estimated as Ψ = {ρ_q,ρ_σ,σ_q,η_q} and the log of the prior probability of observing a given vector of parameters 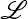(Ψ). The function 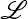(Ψ) summarises what is known about the parameters prior to estimation. The log-likelihood of observing the dataset q^T ≡ {q₁,…,q_T} for a given parameter vector is denoted 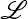(q^T | Ψ).

The likelihood of the data given the parameters factorises to:

The final term in this expression expands as follows:

Computing this expression is difficult because the sequence of conditional densities 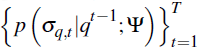has no analytical characterisation. A standard procedure, which we follow, is to substitute the density p (σ_q,t|q^t−1; Ψ) with an empirical draw from it. To obtain these draws, we follow Algorithm 1, which we borrow from Fernández-Villaverde et al (2011).

Algorithm 1

Step 0: initialisation

Sample N particles, 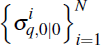from the initial distribution p(σ_q,0|Ψ).

Step 1: prediction

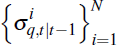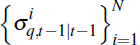Sample N one-step-ahead forecasted particles using , the law of motion for the states (Equation (2)) and the distribution of shocks .

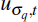Step 2: filtering

Assign each draw 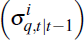the weight 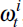, where:

Step 3: resampling

Generate a new set of particles by sampling N times with replacement from 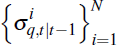using the probabilities 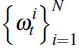. Call the draw 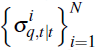. In effect, this step builds the draws 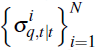recursively from 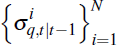using the information on q_t.

If t < T, set t = t + 1 and return to Step 1. Otherwise stop.

Using the law of motion for the terms of trade in Equation (1), we can evaluate 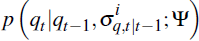for any 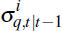. Moreover, from the law of large numbers we know that:

Algorithm 1 provides a sequence of 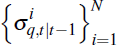for all t. Consequently, the algorithm gives us the information needed to evaluate Equation (C1).

To calculate the posterior distribution of the parameters, we repeat this procedure 25,000 times. At each iteration, we update our parameter draw using a random walk Metropolis-Hastings procedure, scaling the proposal density to induce an acceptance ratio of around 25 per cent. We discard the initial 5,000 draws and conduct our posterior inference on the remaining draws. For each evaluation of the likelihood we use 2,000 particles.