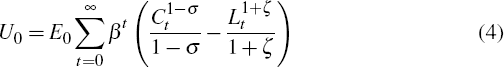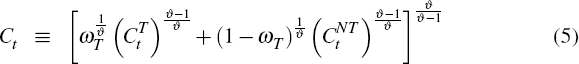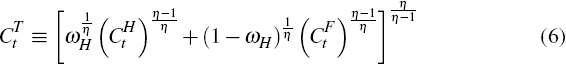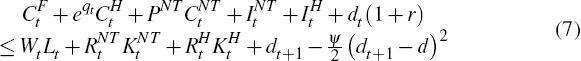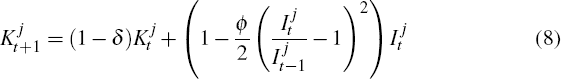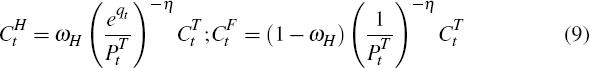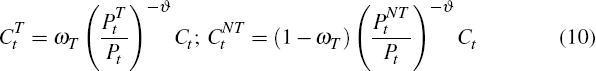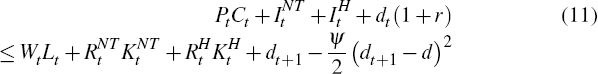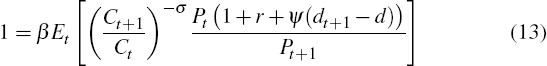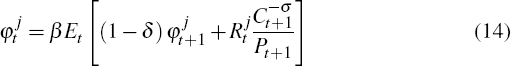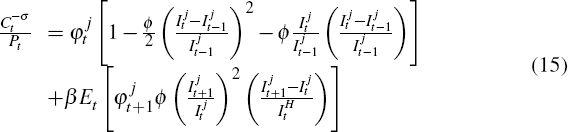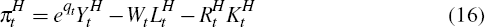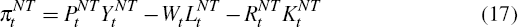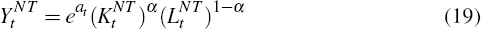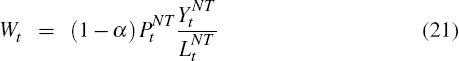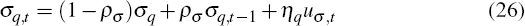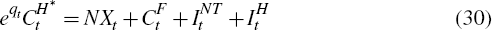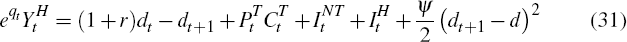RDP 2013-10: Stochastic Terms of Trade Volatility in Small Open Economies 5. The Impact of Volatility Shocks: Theory
August 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 1.06MB
In this section, we embed stochastic terms of trade volatility in an otherwise standard small open economy real business cycle model. In the model, households choose consumption, saving and labour supply to maximise expected lifetime utility. Households consume three goods – non-tradeable, home- and foreign-produced tradeable goods – and can invest in three assets – a one-period risk-free bond traded in international capital markets and physical capital in the two domestic sectors. On the production side, firms seek to maximise profits by producing goods using capital, which is sector-specific, and labour, which is mobile across sectors. As well as terms of trade shocks, we also include productivity shocks in the model. These shocks help the model to match key features of the data, but play little role in the analysis.
5.1 Households
The economy features a representative household that maximises its expected lifetime utility given by:
where C is an aggregate consumption bundle comprising tradeable and non-tradeable goods and L represents the household's supply of labour. The consumption bundle is given by:
where the elasticity of substitution between tradeables and non-tradeables is
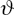 , the weight of tradeables in the consumption
basket is ωT and CNT is the household's
consumption of non-tradeables. CT is the household's
consumption of tradeable goods, which is itself a composite of home- and foreign-produced
tradeable goods:
, the weight of tradeables in the consumption
basket is ωT and CNT is the household's
consumption of non-tradeables. CT is the household's
consumption of tradeable goods, which is itself a composite of home- and foreign-produced
tradeable goods:
where the elasticity of substitution between the two tradeable goods is η, the weight of home-produced goods is ωH, CH is the household's consumption of home-produced tradeable goods and CF is the household's consumption of foreign-produced tradeable goods.
To smooth consumption across time, households have access to three assets: a one-period risk-free bond, denominated in units of the foreign-tradeable good, and physical capital in the non-tradeable and home-tradeable sectors. Reflecting the fact that the domestic economy is small relative to the rest of the world, we assume that the interest rate that agents face when they borrow or lend abroad, r, is exogenous.
Household capital holdings, KNT and KH, are sector specific. We assume that the prices of all capital goods are denominated in units of the foreign-produced tradeable good.
We take the price of the foreign good as numeraire and set it equal to one. With this normalisation, the household's budget constraint is given by:
where eqt is the price of home-produced tradeable goods in terms of foreign-produced tradeable goods – the terms of trade – and PNT is the relative price of non-tradeable goods. The terms of trade is exogenous in the model, while PNT is determined endogenously. INT and IH are investment in the non-tradeable and home-tradeable sectors. W, RNT and RH are the wage rate and return on capital in the non-tradeable and home-tradeable sectors. Note that as labour is mobile between the two sectors, firms in each sector pay the same wage. The final term on the right-hand-side of the equation represents portfolio adjustment costs that households must pay when holding foreign debt at a different level than its steady-state level, d. These ensure that the economy's foreign debt level is stationary and prevent precautionary savings diverging to infinity.[8]
The capital stock of each sector evolves according to the law of motion:
for j = {NT, H}. The parameter δ represents the depreciation rate of capital, while the parameter ϕ controls the size of investment adjustment costs. We include these to ensure that the model economy does not deliver excessive investment volatility in response to shocks.
Household optimisation implies that the demand for home- and foreign-produced tradeable goods is given by:
where
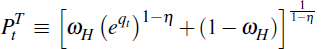 is the traded goods price index. The
demand for tradeable and non-tradeable goods is:
is the traded goods price index. The
demand for tradeable and non-tradeable goods is:
where
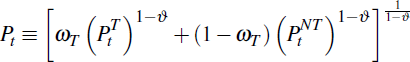 is the
consumer price index (CPI).
is the
consumer price index (CPI).
Using the household's decisions over different good types, we can re-write the household's budget constraint as:
The household's optimal choice over consumption, labour supply and asset holdings implies the following intra and intertemporal conditions:
and
for j ∈ {H,NT} where
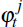 is the Lagrangian associated with capital
in sector j.
is the Lagrangian associated with capital
in sector j.
5.2 Firms
The home-tradeable and non-tradeable sectors both feature perfectly competitive firms that maximise profits, which are given by:
Firms in each sector produce output using a Cobb-Douglas production function:
where
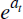 is a productivity shifter that is common
to both sectors.
is a productivity shifter that is common
to both sectors.
Profit maximisation by firms implies that factor prices are equated to the value of marginal products:
5.3 Shock Processes
The model features three exogenous processes. First, productivity evolves according to an AR(1) process:
Second, the terms of trade and its volatility evolve according to the processes described in the empirical section and repeated here for convenience:
The interpretation of the parameters is also as described in the empirical section.
5.4 Equilibrium Definition
A competitive equilibrium is given by an
allocation
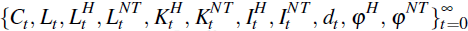 and goods and factor prices
and goods and factor prices
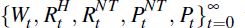 where (i) consumers' satisfy their
optimality conditions
(Equations (12) to (15)) and capital evolves as per Equation (8);
(ii)
firms' zero-profit conditions given in Equations (20) to (23) hold; (iii)
productivity and the terms of trade, at,
qt and σq,t, follow the exogenous
processes in Equations (24) to (26); and (iv) factor and goods markets clear.
where (i) consumers' satisfy their
optimality conditions
(Equations (12) to (15)) and capital evolves as per Equation (8);
(ii)
firms' zero-profit conditions given in Equations (20) to (23) hold; (iii)
productivity and the terms of trade, at,
qt and σq,t, follow the exogenous
processes in Equations (24) to (26); and (iv) factor and goods markets clear.
Regarding factor market clearing, labour is fully mobile across sectors. Hence, its market clearing condition is given by:
Goods market clearing implies that all production in the non-tradeable and tradeable sectors is consumed:
where
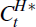 is consumption of the home-produced
tradeable good by foreigners. The latter can be expressed in terms of home
variables only. To do so, we use the equation for the evolution of foreign
debt dt+1−dt =
rdt−NXt where NXt
denotes net exports, defined as nominal exports minus nominal imports:
is consumption of the home-produced
tradeable good by foreigners. The latter can be expressed in terms of home
variables only. To do so, we use the equation for the evolution of foreign
debt dt+1−dt =
rdt−NXt where NXt
denotes net exports, defined as nominal exports minus nominal imports:
Substituting this equation into the tradeable goods market clearing condition and replacing net exports with the debt evolution equation we obtain the condition for home-produced goods market clearing in terms of home variables only:
5.5 Model Solution and Calibration
We solve the model using perturbation methods, taking a third-order approximation of the policy functions of the agents and the law of motion of the exogenous variables around the model's steady state. As Fernández-Villaverde et al (2011) discuss, in models with stochastic volatility it is necessary to take a third-order approximation of the model to capture the effects of volatility shocks independent of the other innovations in the model.[9]
We fix the value of a number of parameters using values generally found in the literature
(Table 4). For households, we set the discount rate, β, equal to 0.99, the inverse of the elasticity of substitution,
σ, and the inverse of the Frisch elasticity, ζ, both equal
to 2, consistent with values commonly used in the literature. We base the values
of
 and η on available estimates
for the elasticity of substitution between traded and non-traded goods. For
the elasticity of substitution between tradeables and non-tradeables,
and η on available estimates
for the elasticity of substitution between traded and non-traded goods. For
the elasticity of substitution between tradeables and non-tradeables,
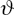 , we use the estimate by Mendoza (1995),
calculated for a sample of industrialised countries, and set that elasticity
equal to 0.74. For the elasticity of substitution between home- and foreign-tradeables,
η, we use the estimate of Corsetti, Dedola and Leduc (2008) and
select a value of 0.85. We set the share of traded goods in the households'
consumption basket, ωT, equal to 0.5, consistent
with the estimates of Stockman and Tesar (1995). We also set the share of home
goods in the tradeable goods basket equal to 0.5.
, we use the estimate by Mendoza (1995),
calculated for a sample of industrialised countries, and set that elasticity
equal to 0.74. For the elasticity of substitution between home- and foreign-tradeables,
η, we use the estimate of Corsetti, Dedola and Leduc (2008) and
select a value of 0.85. We set the share of traded goods in the households'
consumption basket, ωT, equal to 0.5, consistent
with the estimates of Stockman and Tesar (1995). We also set the share of home
goods in the tradeable goods basket equal to 0.5.
| Parameter | Description | Value | Comments |
|---|---|---|---|
| β | Discount factor | 0.99 | Standard value |
| σ | Inverse elasticity of substitution | 2 | Standard value |
| ζ | Inverse of Frisch elasticity | 2 | Standard value |
| ωT | Share of tradeables in consumption basket | 0.5 | As in Stockman and Tesar (1995) |
| ωH | Share of home goods in tradeable consumption basket | 0.5 | Imports share of consumption equals 25 per cent |
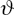 |
Elasticity of substitution between tradeable and non-tradeable goods | 0.74 | As in Mendoza (1995) |
| η | Elasticity of substitution between home- and foreign-tradeable goods | 0.85 | As in Corsetti et al (2008) |
| α | Capital share of income | 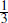 |
Standard value |
| ρa | Persistence of shock to productivity | 0.95 | As in Fernández-Villaverde et al (2011) |
| ψ | Portfolio adjustment cost | 10−3 | Small value to limit impact on dynamics |
On the firm side, we set the capital share of income, α, equal to 1/3 for both sectors. We follow Fernández-Villaverde et al (2011) in setting the persistence of productivity shocks, ρa, equal to 0.95. This choice has little effect on our results as we merely use this shock to calibrate the model. Finally, we set ψ, the portfolio adjustment cost of foreign debt, equal to 10−3 for all the countries. This small value ensures that the foreign debt level is stationary, without significantly affecting the dynamic properties of the model (Schmitt-Grohé and Uribe 2003; Fernández-Villaverde et al 2011).
Conditional on these choices, we pick the remaining three parameters to match moments of the ergodic distribution generated by simulating the model to moments of the data. The three parameters are: (i) σα, the standard deviation of productivity shocks; (ii) ϕ, the adjustment cost of investment; and (iii) d, the parameter that controls the average stock of foreign debt. The moments of the data that we match are: (i) output volatility; (ii) the volatility of investment relative to output; and (iii) the ratio of net exports to output.[10] Table 5 provides the resulting parameter values.
| Parameter | Australia | Brazil | Canada | Mexico | New Zealand | South Africa |
|---|---|---|---|---|---|---|
| d | −2.11 | 1.98 | 3.94 | −3.27 | 2.63 | 7.54 |
| ϕ | 7.89 | 17.20 | 1.87 | 10.88 | 4.04 | 1.66 |
| σα | 1.00 × 10−2 | 1.14 × 10−2 | 1.08 × 10−2 | 1.85 × 10−2 | 1.01 × 10−2 | 1.07 × 10−2 |
In general, the calibration assigns higher values of σα to economies whose output is more volatile. The parameter d helps the model to match the average ratio of net exports to output. Because in the model the real interest rate is greater than the average growth rate, economies who have, on average over the sample, run trade deficits are assigned a value of d that is less than 0, while economies that have run trade surpluses are assigned a value of d that is greater than 0.[11] The parameter ϕ then varies to match the volatility of investment relative to output, conditional on the variances of productivity and the terms of trade.
Footnotes
Portfolio adjustment costs are one of the several ad hoc methods commonly used to close small open economy models. Others include a debt-elastic interest rate premium or a time preference rate that varies with aggregate consumption. Schmitt-Grohé and Uribe (2003) show that all of these methods deliver almost identical dynamics at business-cycle frequencies. Another way of attaining a stationary asset distribution is to assume that the rate of time preference is smaller than the interest rate as in Aiyagari (1994). [8]
Specifically, a first-order approximation eliminates all of the effects of volatility shocks as certainty equivalence holds. A second-order approximation captures the effects of volatility shocks only through their interaction with shocks to the level of the terms of trade. It is only in a third-order (or higher) approximation that stochastic volatility shocks enter as independent arguments in the policy functions. [9]
Because the moments are affected by a non-linear combination of parameters, we choose the parameters to minimise the sum of the quadratic distance between the model moments and the moments from the data. Specifically, for each economy, we simulate a sample of 200 observations and calculate moments based on these observations. We then repeat this procedure 200 times and calculate the mean of each moment across the 200 draws. [10]
In reality, some countries in our sample, such as Australia, have typically run net export deficits while being net debtors to the rest of the world, implying that d is greater than 0. In our model such a persistent pattern could exist if, for example, an economy's expected long-run growth rate was greater than that of the rest of the world (Engel and Rogers 2006). [11]