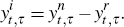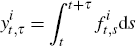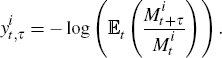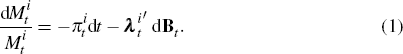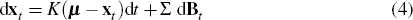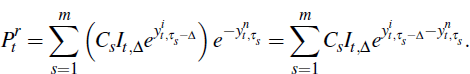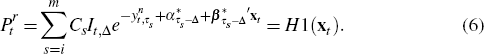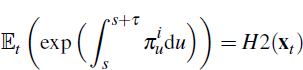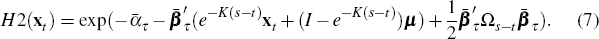RDP 2011-01: Estimating Inflation Expectations with a Limited Number of Inflation-indexed Bonds 2. Model

2.1 Yields and Forward Rates

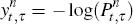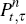To make subsequent discussion clear we first briefly define yields and forward rates in our model. Unless otherwise stated, yields in this paper are gross, zero-coupon and continuously compounded. So, for example, the nominal τ-maturity yield at time t is given by where is the price at time t of a zero-coupon nominal bond paying one dollar at time t + τ. 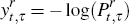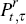The equivalent real yield is given by where is the price at time t of a zero-coupon inflation-indexed bond, which pays the equivalent of the value one time t dollar at time t + τ.^[3] The inflation yield is the difference between the yields of nominal and inflation-indexed zero-coupon bonds of the same maturity. So the inflation yield between time t and t + τ is

The inflation yield describes the cumulative increase in prices over a period. In continuous time, the inflation yield between t and t + τ is related to the inflation forward rates applying over that period by

where 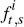is the instantaneous inflation forward rate determined at time t and applying at time s.^[4]

2.2 Affine Term Structure Model

Following Beechey (2008), we assume that the inflation yield can be expressed in terms of an inflation Stochastic Discount Factor (SDF). The inflation SDF is a theoretical concept, which for the purpose of asset pricing incorporates all information about income and consumption uncertainty in our model. Appendix A provides a brief overview of the inflation, nominal and real SDFs.

We assume that the inflation yield can be expressed in terms of an inflation SDF, 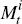, according to

We further assume that the evolution of the inflation SDF can be approximated by a diffusion equation,

According to this model, 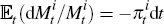, so that the instantaneous inflation rate is given by 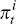. The inflation SDF also depends on the term 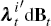. Here B_t is a Brownian motion process and 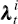relates to the market price of this risk. 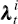determines the risk premium and this set-up allows us to separately identify inflation expectations and inflation risk premia. This approach to bond pricing is standard in the literature and has been very successful in capturing the dynamics of nominal bond prices (see Kim and Orphanides (2005), for example).

We model both the instantaneous inflation rate and the market price of inflation risk as affine functions of three latent factors. The instantaneous inflation rate is given by

where 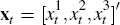are our three latent factors.^[5] Since the latent factors are unobserved, we normalise ρ to be a vector of ones, 1, so that the inflation rate is the sum of the latent factors and a constant, ρ₀. We assume that the price of inflation risk has the form

where λ₀ is a vector and Λ is a matrix of free parameters.

The evolution of the latent factors x_t is given by an Ornstein-Uhlenbeck process (a continuous time mean-reverting stochastic process)

where: K(μ − x_t) is the drift component; K is a lower triangular matrix; B_t is the same Brownian motion used in Equation (1); and Σ is a diagonal scaling matrix. In this instance we set μ to zero so that x_t is a zero mean process, which implies that the average instantaneous inflation rate is ρ₀.

Equations (1) to (4) can be used to show that the inflation yield is a linear function of the latent factors (see Appendix B for details). In particular

where 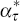and 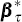are functions of the underlying model parameters. In the standard estimation procedure, when a zero-coupon inflation yield curve exists, this function is used to estimate the values of x_t.

2.3 Pricing Inflation-indexed Bonds in the Latent Factor Model

We now derive the price of an inflation-indexed bond as a function of the model parameters, the latent factors and nominal zero-coupon bond yields, denoted H1(x_t). This function will later be used to estimate the model as described in Section 3.2.

As is the case with any bond, the price of an inflation-indexed bond is the present value of its stream of coupons and its par value. In an inflation-indexed bond, the coupons are indexed to inflation so that the real value of the coupons and principal is preserved. In Australia, inflation-indexed bonds are indexed with a lag of between 4½ and 5½ months, depending on the particular bond in question. This means that for future indexations part of the change in the price level has already occurred, while part is yet of occur. We denote the time lag by Δ and the historically observed increase in the price level between t − Δ and t by I_t,Δ. Then at time t, the implicit nominal value of the coupon paid at time t + τ_s is given by the real (at time t − Δ) value of that coupon, C_s, adjusted for the historical inflation that occurred between t − Δ and t, I_t,Δ, and adjusted by the current market-implied change in the price level between periods t and t + τ_s − Δ using the inflation yield, exp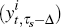. So the implied nominal coupon paid becomes 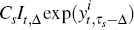. The present value of this nominal coupon is then calculated using the nominal discount factor between t and 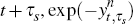. So if an inflation-indexed bond pays a total of m coupons, where the par value is included in the last of these coupons, then the price at time t of this bond is given by

We noted earlier that the inflation yield is given by 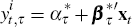so the bond price can be written as

Note that exp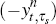 can be estimated directly from nominal bond yields (see Section 3.1). So the price of a coupon-bearing inflation-indexed bond can be expressed as a function of the latent factors x_t as well as the model parameters, nominal zero-coupon bond yields and historical inflation. We define H1(x_t) as the non-linear function that transforms our latent factors into bond prices.

2.4 Inflation Forecasts in the Latent Factor Model

In the model, inflation expectations are a function of the latent factors, denoted H2(x_t). Inflation expectations are not equal to expected inflation yields since yields incorporate risk premia whereas forecasts do not. Inflation expectations as reported by Consensus Economics are expectations at time t of how the CPI will increase between time s in the future and time s + τ and are therefore given by

where 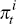is the instantaneous inflation rate at time t. In Appendix B we show that one can express H2(x_t) as

The parameters 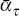and 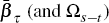are defined in Appendix B, and are similar to 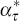and 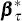from Equation (5).

Footnotes

These are hypothetical constructs as zero-coupon government bonds are not issued in Australia. [3]

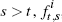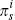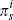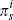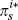At time t, the inflation forward rate at time , is known as it is determined by known inflation yields. The inflation rate, , that will prevail at s is unknown, however, and in our model is a random variable ( can be thought of as the annualised increase in the CPI at time s over an infinitesimal time period). 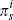is related to the known inflation yield by exp, where is the so-called ‘risk-neutral’ version of (see Appendix B for details). [4]

Note that one can specify models in which macroeconomic series take the place of latent factors, as done for example in Hördahl (2008). Such models have the advantage of simpler interpretation but, as argued in Kim and Wright (2005), tend to be less robust to model misspecification and generally result in a worse fit of the data. [5]