RDP 2011-01: Estimating Inflation Expectations with a Limited Number of Inflation-indexed Bonds 5. Discussion and Conclusion

The model just described is designed to give policy-makers accurate and timely information on market-implied inflation expectations. It has a number of advantages over existing sources for such data, which primarily constitute either break-even inflation derived from bond prices or inflation forecasts sourced from market economists.

As argued, break-even inflation as derived directly from bond prices has a number of drawbacks as a measure of inflation expectations: such a measure gives average inflation over the tenor of the bond, not inflation as at a certain date in the future; Government bonds in Australia are coupon-bearing, which means that yields of similar maturity nominal and inflation-indexed bonds are not strictly comparable; there are very few inflation-indexed bonds on issue in Australia which means that break-even inflation can only be calculated at a limited number of tenors which change over time; inflation-indexed bonds are indexed with a lag which means that their yields also reflect historical inflation, not just future expected inflation; and finally, inflation-indexed bond yields incorporate risk premia so that the level, and even changes in break-even inflation, need not give an accurate read on inflation expectations. Our model addresses each of these issues: we model inflation-indexed bonds as consisting of a stream of payments where the value of each payment is determined by nominal interest rates, historical inflation, future inflation expectations and inflation risk premia. This means we are able to produce estimates of expected future inflation at any time and for any tenor which are free of risk premia and are not effected by historical inflation.

Model-derived inflation expectations also have a number of advantages over expectations from market economists: unlike survey-based expectations they are again available at any time and for any tenor; and they reflect the agglomerated knowledge of all market participants, not just the views of a small number of economists. By contrast, the main drawback of our model is its complexity – break-even inflation and inflation forecasts have their faults but are transparent and simple to measure, whereas our model, while addressing a number of faults, is by comparison complex and difficult to estimate.

Standard affine term structure models, which take as inputs zero-coupon yield curves and give as outputs expectations and risk premia, have existed in the literature for some time. Our main contribution to this literature, apart from the estimation of inflation expectations and inflation risk premia for Australia, is our reformulation of the model in terms of coupon-bearing bond prices instead of zero-coupon yields.

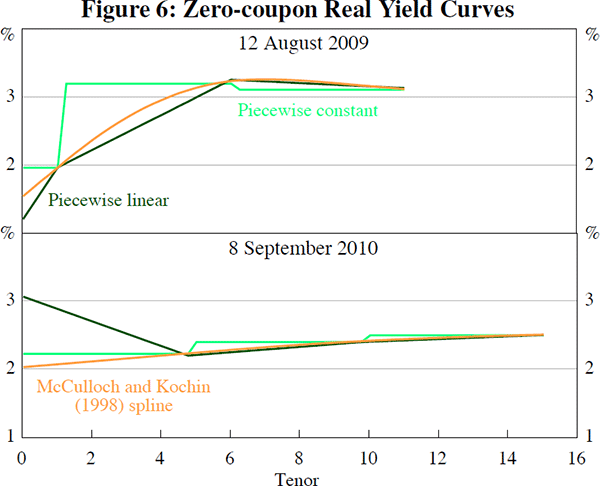
In practice zero-coupon yields are not directly available but must be estimated, so by fitting the affine term structure model directly to prices we avoid inserting a second arbitrary yield curve model between the data and our final model. When many bond prices are available this is only a small advantage as accurate zero-coupon yields can be recovered from the well-specified coupon-bearing yield curve. When only a small number of bond prices are available our method provides a major advantage – one can fit a zero-coupon yield curve to only two or three far-spaced coupon-bearing yields, and indeed McCulloch and Kochin (1998) provide a procedure for doing this, but there are limitless such curves that can be fitted with no a priori correct criteria to choose between them.

The inability to pin down the yield curve is highlighted in Figure 6 which shows three yield curves – one piecewise constant, one piecewise linear and starting from the current six-month annualised inflation rate, and one following the method of McCulloch and Kochin (1998) – all fitted to inflation-indexed bond yields on two different dates. All curves fit the bond data perfectly, as would any number of other curves, so there is nothing in the underlying data to motivate a particular choice, yet different curves can differ by as much as one percentage point. Our technique provides a method for removing this intermediate curve-fitting step and estimating directly with the underlying data instead of the output of an arbitrary yield curve model. The fact that we price bonds directly in terms of the underlying inflation process also allows for direct modelling of the lag involved in inflation-indexation and the impact that historically observed inflation has on current yields, a second major advantage.

In sum, the affine term structure model used in this paper addresses a number of problems inherent in alternative approaches to measuring inflation expectations, and produces plausible measures of inflation expectations over the inflation-targeting era. Given the complexity of the model and the limited number of inflation-indexed bonds on issue, some caution should be applied in interpreting the results. A key finding of the model is that long-term inflation expectations appear to have been well-anchored to the inflation target over most of the sample. Conversely, 1-year-ahead inflation expectations appear to be closely tied to CPI inflation and are more variable than longer-term expectations. Given the relative stability of our estimates of long-term inflation expectations, changes in 5- and 10-year inflation forward rates, and so in break-even inflation rates, are by implication driven by changes in inflation risk premia. As such, our measure has some benefits over break-even inflation rates in measuring inflation expectations.