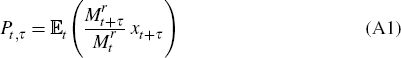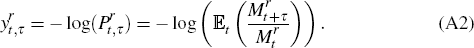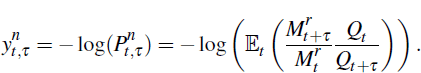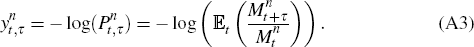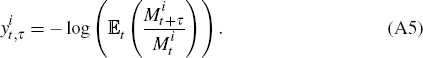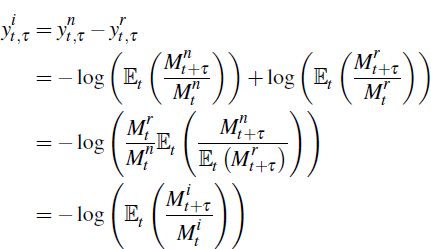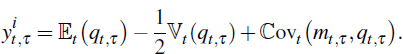RDP 2011-01: Estimating Inflation Expectations with a Limited Number of Inflation-indexed Bonds Appendix A: Yields and Stochastic Discount Factors

The results of this paper revolve around the idea that inflation expectations are an important determinant of the inflation yield. In this appendix we make clear the relationships between real, nominal and inflation yields, inflation expectations and inflation risk premia. We also link these quantities to standard asset pricing models, as discussed, for example, in Cochrane (2005).

A.1 Real Yields and the Real SDF

Let 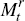be the real SDF or pricing kernel, defined such that

holds for any asset, where P_t,τ is the price of the asset at time t which has (a possibly random) pay-off x_t+τ occurring at time t + τ. A zero-coupon inflation-indexed bond maturing at time t + τ is an asset that pays one real dollar, or equivalently one unit of consumption, for certain. That is, it is an asset with payoff x_t+τ ≡ 1. If we define the (continuously compounded) gross real yield by 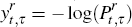, that is, as the negative log of the inflation-indexed bond price, we can use Equation (A1) with x_t+τ = 1 to write

This defines the relationship between real yields and the continuous time real SDF.

A.2 Nominal Yields and the Nominal SDF

A zero-coupon nominal bond maturing at time t + τ is an asset that pays one nominal dollar for certain. If we define Q_t to be the price index, then the pay-off of this bond is given by x_t+τ = Q_t/Q_t+τ units of consumption. For example, if the price level has risen by 10 per cent between t and t + τ, so that Q_t+τ = 1.1 × Q_t, then the nominal bond pays off only 1/1.1 ≈ 0.91 units of consumption. Taking x_t+τ = Q_t/Q_t+τ in Equation (A1), we can relate the gross nominal yield 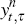to the nominal bond price 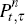and the continuous time real SDF by

Motivated by this result, we define the continuous time nominal SDF by 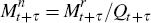, so that

A.3 Inflation Yields and the Inflation SDF

The inflation yield is defined to be the difference in yield between a zero-coupon nominal bond and a zero-coupon inflation-indexed bond of the same maturity

As in Beechey (2008), we define the continuous time inflation SDF, 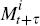, such that the pricing equation for inflation yields holds. That is, such that

All formulations of 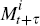which ensure that Equations (A2), (A3) and (A4) are consistent with Equation (A5) are equivalent from the perspective of our model, since only inflation yields are seen by the model. One such formulation is to define the inflation SDF as

We can then obtain Equation (A5) by substituting Equations (A2) and (A3) into Equation (A4) and using the definition of the inflation SDF given in Equation (A6).

In this case we have

as desired. If one assumed that 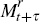and Q_t+τ were uncorrelated, a simpler formulation would be to take 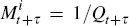. Since 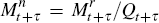, in this case we would have 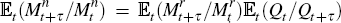so that 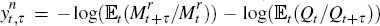and 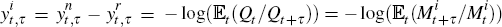as desired.

A.4 Interpretation of Other SDFs in our Model

We model 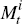directly as 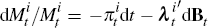, where we take 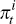as the instantaneous inflation rate and 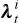as the market price of inflation risk. Although very flexible, this set-up means that in our model the relationship between different stochastic discount factors in the economy is not fixed.

In models such as ours there are essentially three quantities of interest, any two of which determine the other: the real SDF, the nominal SDF and the inflation SDF. As we make assumptions about only one of these quantities we do not tie down the model completely. Note that we could make an additional assumption to tie down the model. Such an assumption would not affect the model-implied inflation yields or inflation forecasts however, which are the only data our model sees, and so in the context of our model would be arbitrary.

Note that this situation of model ambiguity is not confined to models of inflation compensation such as ours. The extensive literature which fits affine term structure models to nominal yields contains a similar kind of ambiguity. Such models typically take the nominal SDF as driven by 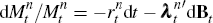where once again the real SDF and inflation process are not explicitly modelled, so that, similar to our case, the model is not completely tied down.

A.5 Inflation Expectations and the Inflation Risk Premium

Finally, we link our inflation yield to inflation expectations and the inflation risk premium. The inflation risk premium arises because people who hold nominal bonds are exposed to inflation, which is uncertain, and so demand compensation for bearing this risk. If we set 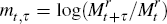and 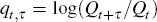which are both assumed normal, and use the identity 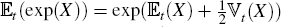where X is normally distributed and 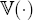is variance, we can work from Equation (A4) to derive

The first term above is the expectations component of the inflation yield while the last two terms constitute the inflation risk premium (incorporating a ‘Jensen's’ or ‘convexity’ term).