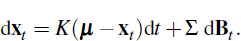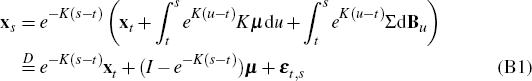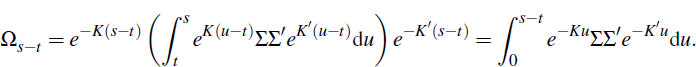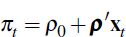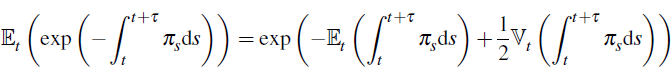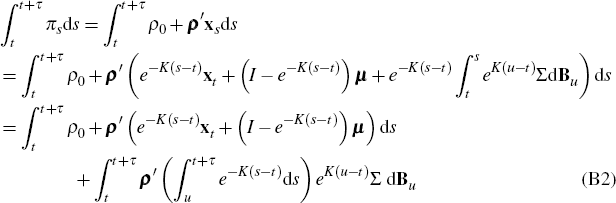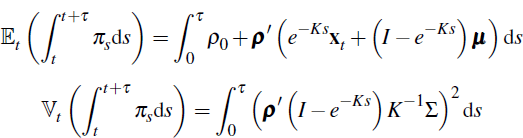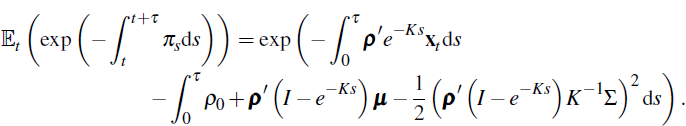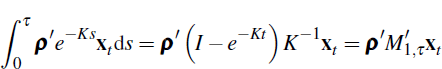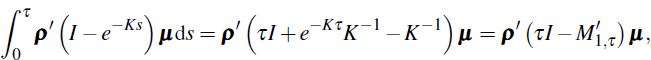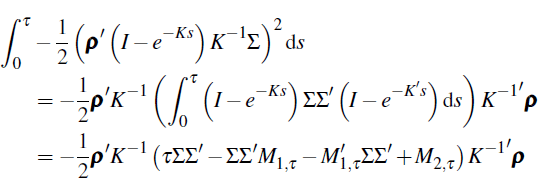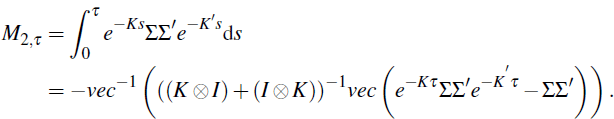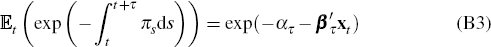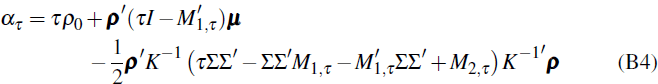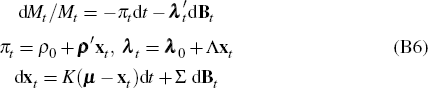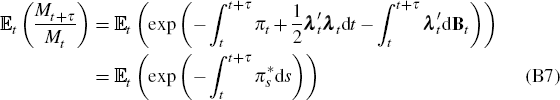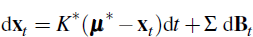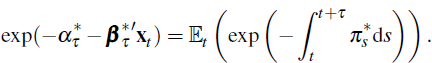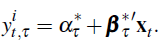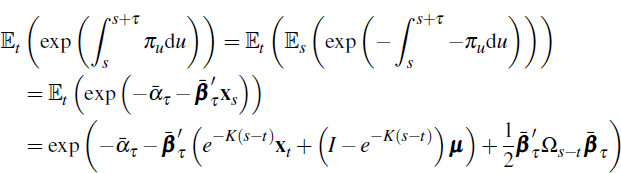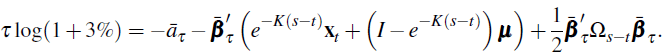RDP 2011-01: Estimating Inflation Expectations with a Limited Number of Inflation-indexed Bonds Appendix B: The Mathematics of Our Model

We first give some general results regarding affine term structure models, then relate these results to our specific model and its interpretation.

B.1 Some Results Regarding Affine Term Structure Models

Start with the latent factor process

Given x_t we have, for s > t (see, for example, p 342 of Duffie (2001))

where 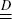denotes equality in distribution and 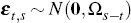with

Further, if we define

then since 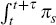is normally distributed,

with

where we have used a stochastic version of Fubini's theorem to change the order of integration (see, for example, p 109 of Da Prato and Zabczyk (1992)). Evaluating the inner integral of line (B2), using Itô's Isometry (see, for example, p 82 of Steele (2001)) and making the change of variable s = t + τ − u we have

where for x a vector we define x² = x′² as the vector dot-product x′x. Hence

Now for 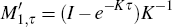we have,

while

and

where from Kim and Orphanides (2005) for example,

Putting this together we have

with

Equivalent formula are available in Kim and Orphanides (2005).

B.2 Bond Price Formula

If we model the SDF according to

then the price of a zero-coupon bond at t paying one dollar at t + τ is given by (see, for example, Cochrane (2005))

where 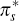is like π_s in Equation (B6) above but with

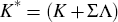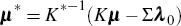where and (Here 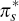is the ‘risk neutral’ version of π_s.) Hence we can price bonds via Equation (B3) using K^* and μ^* in place of K and μ in Equations (B4) and (B5). We can write Equation (B7) as

In terms of the inflation yield from Equation (A5) this can be written as

B.3 Inflation Forecast Formula

Inflation expectations are reported in terms of percentage growth in the consumer price index, not average inflation (the two differ by a Jensen's inequality term). As such, expectations at time t of how the CPI will grow between time s > t and time s + τ in the future correspond to a term of the form

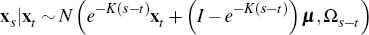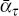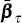where the last line follows since Here and are equivalent to α_τ and β_τ from Equations (B4) and (B5) respectively but with the market price or risk λ_τ set to zero and using −ρ₀ and −ρ in place of ρ₀ and ρ. So if the CPI is expected to grow by 3 per cent between s and s + τ for example, we would have