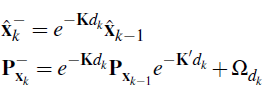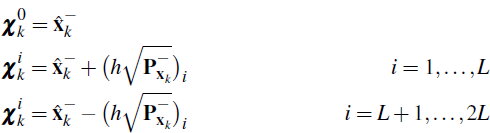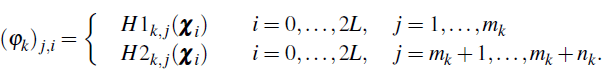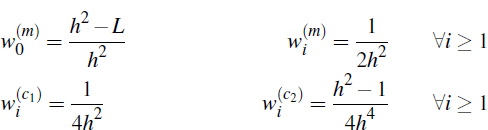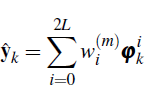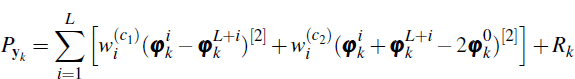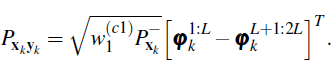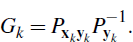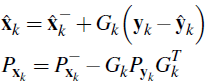RDP 2011-01: Estimating Inflation Expectations with a Limited Number of Inflation-indexed Bonds Appendix C: Central Difference Kalman Filter
March 2011
- Download the Paper 480KB
The central difference Kalman filter is a type of sigma-point filter. Sigma-point filters deal with non-linearities in the following manner:
- First, a set of points around the forecast of the state is generated. The distribution of these points depends on the variance of the forecast of the state.
- The measurement equations (functions H1(xt) and H2(xt)) are used to calculate a set of forecast observation points. This set of points is used to estimate a mean and variance of the data forecasts.
- The mean and variance of the data forecasts are then used to update the estimates of the state and its variance.
The algorithm we use is that of an additive noise central difference Kalman filter, the details of which are given below. For more detail on sigma-point Kalman filters see van der Merwe (2004).
Step 1: Initialise the state vector and its covariance matrix to their unconditional expected values,
Step 2: Loop over k = 1 : n where n is the length of our data set.
Step 2.k.1: Time-update equations:
where dk is the time in years between data point k and data point k − 1.
Step 2.k.2: Create the sigma points,
where 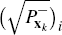 is the ith column of the matrix square root of
is the ith column of the matrix square root of 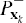 , L is the number
of latent factors and h is the central difference step size, which
is set to
, L is the number
of latent factors and h is the central difference step size, which
is set to 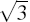 .
.
Step 2.k.3: Propagate the sigma points through the pricing functions 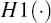 and
and 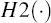 .
Let mk be the number of observed inflation-indexed bond
prices in period k. Let nk be the number of observed
inflation forecasts in period k. For each observed price j
= 1,...,mk we propagate each sigma point
.
Let mk be the number of observed inflation-indexed bond
prices in period k. Let nk be the number of observed
inflation forecasts in period k. For each observed price j
= 1,...,mk we propagate each sigma point 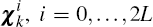 through the pricing function
for bond j in period k,
through the pricing function
for bond j in period k, 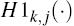 . For each observed forecast
j = mk + 1,…,mk + nk
we propagate each sigma point
. For each observed forecast
j = mk + 1,…,mk + nk
we propagate each sigma point 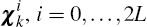 through the pricing function for forecast
j in period k,
through the pricing function for forecast
j in period k, 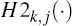 . Denote the output by φk,
which is a matrix of dimension nk + mk
by 2L + 1 with elements
. Denote the output by φk,
which is a matrix of dimension nk + mk
by 2L + 1 with elements
Denote the ith column of φk by 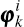 .
.
Step 2.k.4: Observation update equations. For weightings of
the estimate of the price vector is given by a weighted average of the 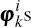
and the estimated covariance matrix of 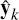 is given by
is given by
where Rk is the covariance matrix of the noise present in the
observed prices. Here 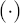 [2] denotes the vector outer product.
[2] denotes the vector outer product.
Next the estimate of the covariance between the state estimate and the price estimate is given by
Step 2.k.5: Calculate the Kalman gain matrix Gk
Step 2.k.6: Update the state estimates,
where yk is the vector of observed prices.