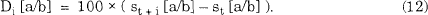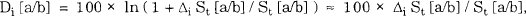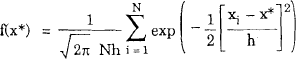RDP 8906: A Random Walk Around the $A: Expectations, Risk, Interest Rates and Consequences for External Imbalance V. Skewness
October 1989
- Download the Paper 1.72MB
This section provides evidence about the skewness of the $A against a range of currencies and against the trade-weighted index (TWI). There have been many studies examing the skewness of exchange rate returns over very short horizons (a day or less – see for example, Bewley et.al., (1987)). By contrast, our analysis examines skewness over a week and four weeks because we are interested in an horizon relevant to those investing in Australian assets for substantially longer than a day. In all cases we examine the behaviour of the random variable Di [a/b], defined as
There are two reasons for studying Di [a/b]. Firstly, defining Δi St [a/b] = St + i [a/b] − St [a/b], it follows that
provided Δi St/St is small compared to 1. Hence, Di [a/b] is approximately the percentage return from converting currency a into currency b for i periods. Secondly, by definition, Di [b/a] ≡ − Di [a/b] and so – Di [a/b] is approximately the percentage return from converting currency b into currency a for i periods.
In Tables 5 – 8, we examine the sample values of the third central moment (tcm) of Di [a/b], i.e., E {Di [a/b] − E Di [a/b]}3, for a range of currencies and time periods. Table 5 demonstrates that for weekly changes, the $A may have been negatively skewed against most currencies since 1979, but that this skewness has become much larger and statistically significant since the $A was floated in Dec 83.[23] Since Jan 86, this skewness has remained large (and may have become larger – see the comparison of two week changes in Table 6).
| Currency a | ||||||
|---|---|---|---|---|---|---|
| $US | ¥ | £ | DM | $C | TWI | |
| Period | ||||||
| Jan 79 – Dec 83 | −3.9 | −4.5 | −3.3 | −5.9 | −3.9 | −3.3 |
| Jan 84 – Apr 89 | −6.1** | −9.8** | −8.8* | −8.7** | −5.3** | −6.2** |
| Jan 86 – Apr 89 | −5.6* | −12** | −7.6 | −12* | na | −6.4* |
| Periods 79 – 83 and 84 – 89: From dataset A. | Period 86 – 89: From dataset B. | |||||
* Different from zero at 10% level of significance |
||||||
| $US | ¥ | £ | DM | TWI | |
|---|---|---|---|---|---|
| Period | |||||
| One week | −6.11** (2.49) |
−9.75** (4.07) |
−8.83* (4.92) |
−8.74** (4.39) |
−6.22** (2.87) |
| Two weeks | −10.85* (6.52) |
−23.21** (10.33) |
−16.99 (12.02) |
−16.93 (11.92) |
−13.75** (6.23) |
| Four weeks | −40.10 (31.70) |
−79.20* (46.33) |
−88.74 (69.64) |
−69.89 (48.16) |
−39.05* (22.22) |
| $US | ¥ | £ | DM | TWI | |
|---|---|---|---|---|---|
| Period | |||||
| One week | −5.57* (2.96) |
−12.04** (6.15) |
−7.63 (4.94) |
−11.67* (6.29) |
−6.42* (3.42) |
| Two weeks | −15.25* (8.67) |
−38.09* (20.06) |
−25.67 (18.46) |
−38.51* (22.52) |
−19.19* (10.59) |
| Month (22 working days) | −40.61 (32.52) |
−119.76 (90.94) |
−51.69 (60.64) |
−114.17 (87.27) |
− 54.97 (38.64) |
Standard errors in brackets |
|||||
| Currency a | ||||||
|---|---|---|---|---|---|---|
| $A | $US | ¥ | £ | DM | $C | |
| Currency b | ||||||
| $A | • | −6.1** | −9.8** | −8.8* | −8.7** | −5.3** |
| $US | 6.1** | • | −1.9 | −2.0 | −1.4 | 0.0 |
| ¥ | 9.8** | 1.9 | • | 0.7 | 0.0 | 1.6 |
| £ | 8.8* | 2.0 | −0.7 | • | −0.3 | 1.4 |
| DM | 8.7** | 1.4 | 0.0 | 0.3 | • | 1.0 |
| $C | 5.3** | 0.0 | −1.6 | −1.4 | −1.0 | • |
| Currency a | ||||||
|---|---|---|---|---|---|---|
| $A | $US | ¥ | £ | DM | $C | |
| Currency b | ||||||
| $A | • | −40 | −79* | −89 | −70+ | −22 |
| $US | 40 | • | −23+ | −27 | −10 | 0.9 |
| ¥ | 79* | 23+ | • | −1.2 | −0.3 | 20 |
| £ | 89 | 27 | 1.2 | • | −3.4 | 18 |
| DM | 70+ | 10 | 0.3 | 3.4 | • | 6.8 |
| $C | 22 | −0.9 | −20 | −18 | −6.8 | • |
Dataset A: weekly (Friday) data, Jan 84 – Apr 89. |
||||||
| Currency a | |||||
|---|---|---|---|---|---|
| $A | $US | ¥ | £ | DM | |
| Currency b | |||||
| $A | • | −5.6* | −12** | −7.6 | −12* |
| $US | 5.6* | • | −1.3 | −0.2 | −0.7 |
| ¥ | 12** | 1.3 | • | 0.1 | −0.1 |
| £ | 7.6 | 0.2 | −0.1 | • | −0.3 |
| DM | 12* | 0.7 | 0.1 | 0.3 | • |
| Currency a | |||||
|---|---|---|---|---|---|
| $A | $US | ¥ | £ | DM | |
| Currency b | |||||
| $A | • | −41 | −120+ | −52 | −114+ |
| $US | 41 | • | −18 | −1.5 | −7.9 |
| ¥ | 120+ | 18 | • | 22 | 3.3 |
| £ | 52 | 1.5 | −22 | • | −7.5 |
| DM | 114+ | 7.9 | −3.3 | 7.5 | • |
Dataset B: daily data, Jan 86 – Apr 89. |
|||||
Tables 7 and 8 show that the $A is much more skewed than other currencies. This is clear both from the size of the point estimates of the third central moment, and from their level of significance. These conclusions are supported by the results of a non-parametric test shown in Table 9. This test, which is described in Appendix D, has the advantage that under the null hypothesis, it is not necessary to assume that Di [a/b] is normally distributed. The test is also approximately valid when the observations of Di [a/b] come from different distributions. Figures 8 and 9 show the distributions of Di [TWI/$A], Di [¥/$A] and Di [¥/$US] for i = one week, and for i = four weeks since Jan 86.[24] In Figure 9, Di [¥/$US] is chosen because it is one of the most skewed distributions which does not involve the $A (see Table 8). In both Figures, the significant proportion of big depreciations of the $A is clearly not matched by an equal proportion of big appreciations.
| Currency a | |||||
|---|---|---|---|---|---|
| $A | $US | ¥ | £ | DM | |
| Currency b | |||||
| $A | • | (−) 5** |
(−) 3** 2* |
(−) 2* |
(−) 3** 1* |
| $US | (+) 5** |
• |
(−) 1* |
0 |
(−) 1* (+) 1* |
| ¥ | (+) 3** 2* |
(+)1* |
• |
0 |
0 |
| £ | (+) 2* | 0 | 0 | • | 0 |
| DM | (+) 3** 1* |
(+)1* (−)1* |
0 |
0 |
• |
Dataset B: daily data, Jan 86 – Apr 89. |
|||||
Distribution of weekly and four weekly returns on the $A against the TWI
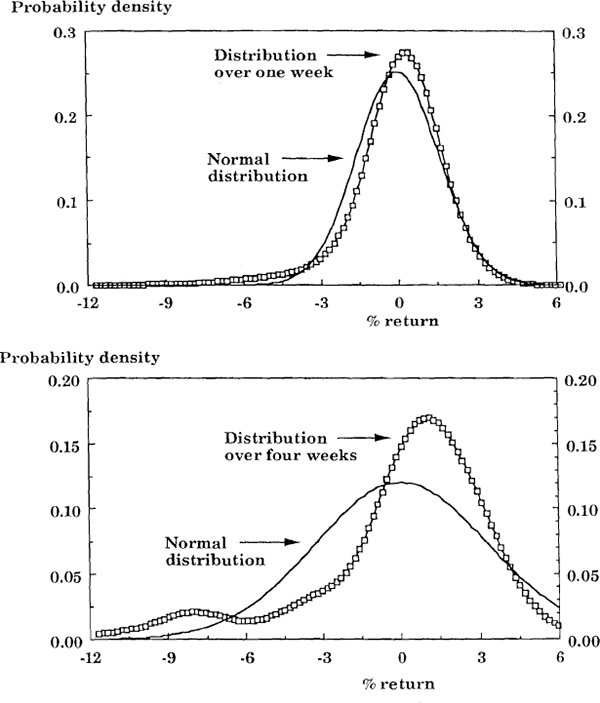
In both cases, the normal distribution has the same mean and variance as the actual distribution. Results are derived from dataset B: daily rates Jan 86 – Apr 89.
Distribution of weekly and four weekly returns: ¥/$A and ¥/$US
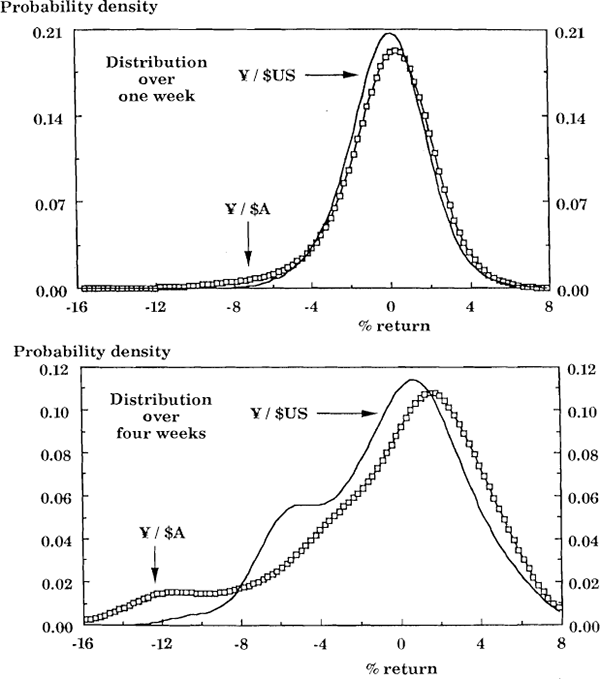
The ¥ / $US distributions have been shifted by + 0.08% and + 0.38% respectively, so that their means coincide with the means of the ¥ / $A distributions. Results are derived from dataset B: daily rates Jan 86 – Apr 89.
In this section, we have focussed our attention particularly on the period since Jan 86. Since then, most of the exogenous “news” from Australia's terms of trade has been favourable. The terms of trade had already fallen from 100.6 in Mar Q 85 to 91.9 in Dec Q 85. In 86, the fall continued at a slower rate to a low of 87.0 in Mar Q 87, then climbed rapidly to 113.4 by Mar Q 89 (from RBA Bulletin, Table K.3, Dec 88 and Jun 89). So, it is hard to sustain the argument that since Jan 86 Australia's external sector has suffered a series of unfavourable exogenous shocks which have required a succession of falls in the $A.[25]
Table 10 [26] provides evidence on the possible causes of the ten largest weekly falls of the $A from Jan 86 to Apr 89.[27] The large fall which followed the 1987 stockmarket crash suggests that the exchange rate is (sometimes) very sensitive to external shocks. Most of the other events which were identified seem related to the unexpectedly slow progress being made by the real economy onto a sustainable net external debt/ GDP path.[28] This comment applies most obviously to the second and third events as well as to the two current account announcements. We return to this theme in the final section of the paper.
| Week | % fall | Reason – judged by reports during the week in the Australian Financial Review. |
|---|---|---|
| 31 Jan – 7 Feb 86 | 3.2 | No obvious event. |
| 30 May– 6 June 86 | 4.6 | No obvious event. “US investors are beginning to get nervous about the magnitude of the economic problems facing the Australian Government.” Lead article, 5 June. This article is almost exclusively about adjustment to the external trade imbalance. |
| 20 – 27 June 86 | 3.6 | On 24 June, The Wall Street Journal editorial page is quoted asking: “Will Australia become the next Banana Republic?” |
| 27 June – 4 July 86 | 5.0 | Rumours that Mr. Keating had resigned as Treasurer. Removal of exemptions for withholding tax. Push by unions for wider superannuation coverage. Waterside Workers nationwide strike (resolved on 3 July). |
| 18 – 25 July 86 | 4.5 | Unexpectedly large June quarter CPI figure announced (CPI up 1.7%). |
| 15 – 22 Aug 86 | 3.1 | Unexpectedly large July current account deficit announced ($1.35bn). |
| 9 – 16 Jan 87 | 4.2 | No obvious event. “Sudden change of sentiment in foreign exchange market.” Front page, 14 Jan. Perhaps related to the EMS realignment occurring at the time. |
| 23 – 30 Oct 87 | 6.7 | Delayed reaction to stock market crash (on 19, 20 Oct). “The world stockmarket crash has …[left] Australia exposed because of its high foreign debt burden and dependence on commodity exports.” Front page, 30 Oct. |
| 24 June – 1 July 88 | 2.9 | Global strength of $US |
| 10 – 17 Feb 89 | 6.8 | Unexpectedly large Jan current account deficit announced ($1.54bn). “The dollar is now diminishing our competitiveness. When demand conditions moderate I expect, and indeed hope, that the dollar will fall. And certainly, the day that starts we will not be standing in the way of stopping it.” Mr. Keating, 16 Feb. |
|
The data consists of 170 weekly changes. The median change is 0.19%. Of the ten largest deviations from this median (values of yj from Appendix D), all ten are falls. They form the basis for this Table. |
||
Footnotes
In common with others (e.g., Bewley et. al. 1987), we find evidence of leptokurtosis (which should be a disease, but in fact means a distribution with a larger fourth central moment than the normal distribution with the same variance). We find leptokurtosis in weekly log changes of the $A against most currencies since the float but not before it. [23]
Of course, one could claim that the outcome was unfavourable compared to what was expected. But for the outcome to have appeared unfavourable, the expectations must have been for a massive improvement in the terms of trade. We are not aware of any such optimistic expectations. [25]
We use an Australian financial newspaper for Table 10 rather than a foreign one because Wong (1988) finds that most of the movements in the $A/$US exchange rate occur while the foreign exchange markets are open in Australia. [26]
As Frank Milne pointed out to us, the Table suffers from an important weakness. Rather than examining all events of a particular kind (e.g. all current account announcements) to test whether, on average, unexpected outcomes have an impact on the exchange rate, we search for the ‘causes’ of the biggest falls, ex post. We did use Dataset B to examine the percentage change in the $A against the TWI from the day before monthly current account announcements to four working days after (st + 4 − st − 1, where t is the day of the release). We find a correlation coefficient between (st + 4 − st − 1) and the nominal $A value of the announced current account deficit, of −0.39. Surprisingly, we find an average value of (st + 4 − st − 1) of 0.27% over the 39 announcements in the sample, compared to a mean weekly change for the whole sample of 0.006%. So, on average, during a week which included a current account announcement, the $A appreciated substantially more than during an arbitrarily chosen week. [27]
The debt/GDP ratio will increase (potentially without bound) if net exports are in deficit (as they are in Australia) and if the nominal interest rate exceeds the nominal growth rate of GDP (which, at least for $A-denominated debt, it does). Therefore, at present, the real economy is on an unsustainable debt/GDP path. [28]