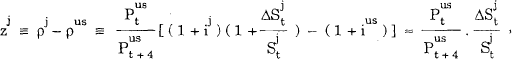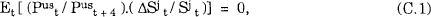RDP 8906: A Random Walk Around the $A: Expectations, Risk, Interest Rates and Consequences for External Imbalance Appendix C

This appendix describes how the estimates in Table 3 were derived. We measure time in weeks and use exchange rate Dataset A from 6 Jan 84 to 21 Apr 89. We do not have interest-rate data for each country, so we use the approximation (1 + i^j) ≈ 1, for all j. Then,

where ΔS^j_t ≡ S_{t + 4} [j/$US] − S_t [j/$US]. Since the period of analysis is four weeks, the approximation, (1 + i^j) ≈ 1, introduces an average error of the order of (or less than) 1%. Further, as noted previously, almost all the variation in z^j arises from exchange rate variation.

Price data comes from monthly US CPI data from OECD Main Economic Indicators (various issues). All Fridays in any given month are assigned the price index for that month. To evaluate cov (z^A, ρ^us), we require E_t[P^us_t/P^us_{t + 4}]. We assume a simple form of adaptive expectations: E_t[P^us_t/P^us_{t + 4}] = [P^us_{t − 16}/P^us_{t − 12}]. The sixteen week lag is used to ensure that only published price indices are used in forming the expectation. A more sophisticated expectation formation assumption^[45] should presumably reduce P^us_t/P^us_{t + 4} − E_t[P^us_t/P^us_{t + 4}], and hence reduce our estimate of cov (z^A, ρ^us ). It suits our purposes if our estimate is an overestimate. To evaluate the other covariances and the variance, we assume

because, over four weeks, exchange rates changes for the currencies we consider are well approximated as an unpredictable random variable with zero mean. We have established that using the one month forward discount in equation (C.1) as the expected depreciation of the $A against the $US makes only a small change to our estimate of var(z^A) – it increases the estimate from 11.9×10⁻⁴ to 12.5×10⁻⁴.

Footnote

Given the dramatic change in the income velocity of money in the 1980s (see, for example, Friedman, 1988 – especially Figure 2), ex ante it might have been quite difficult to have had more accurate inflation expectations than the backward looking ones used here. [45]