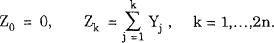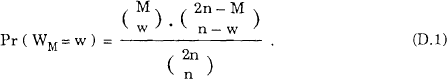RDP 8906: A Random Walk Around the $A: Expectations, Risk, Interest Rates and Consequences for External Imbalance Appendix D

We describe here a non-parametric statistical test for the skewness of the distribution D_i [a/b]. Assume we have a sample with an odd number (2n + 1) of independent^[46] observations from D_i [a/b].^[47] Order the sample from the most negative to the most positive and define d_j as the j^th observation (so d_j−1 ≤ d_j ≤ d_{j + 1} for 1 < j < 2n + 1). d_{n + 1} is the median of the sample. Define y_j = d_j − d_{n + 1}, j = 1,…, 2n+1, and form the random variables Y_k, k = 1,…,2n, defined by Y_k = − 1 when y_j is the k^th largest of the y_j 's in absolute value and y_j is negative; Y_k = 1 when y_j is the k^th largest of the y_j 's in absolute value and y_j is non-negative. Finally, define the random walk Z_k, by

Provided that d_j ≠ d_{n + 1} for all j ≠ n + 1,^[48] there are exactly n ‘−1’ values and n ‘+1’ values taken by the random variables Y_k , k = 1,…,2n, and hence the random walk, Z_k, walks from Z₀ = 0 to Z_2n = 0. Crucially, under the null hypothesis that the distribution D_i [a/b] is symmetric, all distributions of the n ‘−1’ values and n ‘+1’ values among the random variables Y_k , k = 1,…,2n, are equally likely and all walks Z_k from Z₀ = 0 to Z_2n = 0 are also equally likely. By contrast, if D_i [a/b] is negatively (positively) skewed, Z_k, k = 1,…,2n will be more likely to walk to large negative (positive) values before returning to zero when k = 2n. No specific assumption about the distribution of D_i [a/b] is necessary – the null hypothesis is simply that D_i [a/b] is symmetric.

Define the random variable W_M as the number of the random variables Y_k , k = 1,…,M, which take the value ‘−1’. Under H₀, Pr(W_M = w), is

Our one-sided test for negative [positive] skewness involves evaluating the probability, Pr(W_M ≥ w) [ Pr(W_M ≤ w)]. For the results in Table 9, n = 84, and M = 10 was chosen. Evaluation of (D.1) gives: Pr(W₁₀ = 0) = Pr(W₁₀ = 10) = 0.0007, Pr(W₁₀ ≤ 1) = Pr(W₁₀ ≥ 9) = 0.0090, Pr(W₁₀ ≤ 2) = Pr(W_l0 ≥ 8) = 0.0494. Thus, sample values of W₁₀ of 9 or 10 (0 or 1) imply rejection of H₀ at the 1% level of significance against the alternative of negative (positive) skewness, while a value of 8 (2) implies rejection at the 5% level. Sample values 3 ≤ W₁₀ ≤ 7 are insignificant.^[49]

As discussed in Appendix B, in general the distribution of D_i [a/b] at time t (D^t_i [a/b]) depends on observations of s_{τ + i} − s_τ, τ < t. Clearly, this invalidates our assumption of the independence of the observations, and our test of skewness must be modified. The null hypothesis is now that each of the D^t_i [a/b] distributions is symmetric with a common mean, μ. Under this null, the distribution of W₁₀ depends on how different are the distributions D^t_i [a/b], t = 1,…, 2n+1. At one extreme is the case already examined when all the distributions are identical, and each Y_k, k = 1,…,2n has an equal chance of coming from any of the D^t_i [a/b], t = 1,…,2n+1. At another extreme, assume that under the null there are only two distinct (symmetrical) distributions: for ten particular times, t(j), j = 1,…,10, the distributions D^t(j)_i [a/b] ≡ D⁺, and at all other times, τ, τ ≠ t(j), j = 1,…,10, D^τ_i [a/b] ≡ D^*. D^* is assumed to have all its probability weight “near” μ while D⁺ is assumed to have all its probability weight in two tails “far from” μ, so that D^* and D⁺ have no overlap. In this contrived case, we can be sure that for j = 1,…,10, Yj must come from D⁺ and hence from the ten particular times, t(j), j = 1,…,10. Then under the null hypothesis, Pr(W₁₀ = w) is simply

Equation (D.2) gives: Pr(W₁₀ = 0) = Pr(W₁₀ = 10) = 0.00098, Pr(W₁₀ ≤ 1) = Pr(W₁₀ ≥ 9) = 0.011, Pr(W₁₀ ≤ 2) = Pr(W₁₀ ≥ 8) = 0.055. Thus, even in this extreme case, the critical values of W₁₀ are only changed slightly.

Footnotes

The assumption of independence makes the analysis exact. We examine the removal of this assumption at the end of this appendix. [46]

If we have an even number (2n + 2) of independent observations, we define d_j as described, but now define y_j = dj − (d_{n + 1} + d_{n + 2})/2, j = 1,…, 2n+2. The random variables Y_k , k = 1,…,2n, are defined as described and equation (D.1) is again the basis of our non-parametric test for the skewness of D_i [a/b]. [47]

With the exception of the TWI data (which is quoted to three figures), all our exchange rate data is quoted to (at least) four significant figures, so it is unlikely that any two values of d_j would be the same. [48]

An alternative test based on the distribution of the maximum (or minimum) value taken by the walk, Z_k, k = 1,…,2n, was also examined but found to have little power. One of us (J. S.) examined the skewness of the data assuming that D₅ [a/b] has a distribution of the stable Paretian form, The results are similar to those reported here. [49]