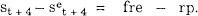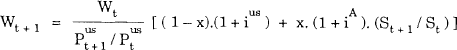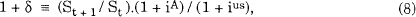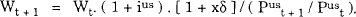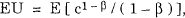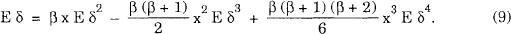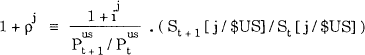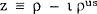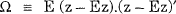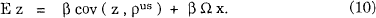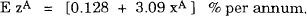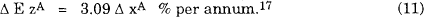RDP 8906: A Random Walk Around the $A: Expectations, Risk, Interest Rates and Consequences for External Imbalance III. The Risk Premium
October 1989
- Download the Paper 1.72MB
To begin, we briefly use some of the results from the previous section to provide measures of the nominal risk premium. Figure 3 shows a decomposition suggested by Froot and Frankel (1989) of the average market participant's expectational error, st + 4 − set + 4, into the nominal risk premium, rp = set + 4 − ft, 1 month, and the forward rate error, fre = st + 4 − ft, 1 month,[7]
Nominal risk premium of the average market participant and the forward rate error
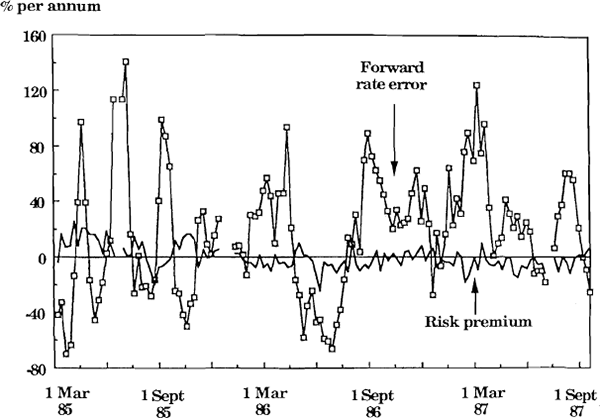
For the estimate of the risk premium in Figure 3 to be accurate, it is necessary that the ‘true investor expectation’ is measured with no error – a requirement that seems rather stringent (see footnote 5). We can alternatively use equation (5) in Table 2 to test the null hypothesis that the risk premium is zero (equivalent to Δ set + 4 = fdt, 1 month; hence the null hypothesis is α = 0, β = 1). Applying this test to our whole sample survey at a 5% level of significance, we accept this null of zero risk premium.[8]
In the rest of this section we provide a priori estimates of the risk premium necessary to induce a US consumer-investor to hold a proportion of wealth in short-term Australian denominated interest-bearing bills. We present two simple single-period models in which a US consumer-investor maximizes end-of-period expected utility. This utility is derived from consumption of a basket of goods. The period of the model is four weeks.
In the first model, four weeks is assumed sufficiently short that the price index for the basket of goods at the end of this time, Pust + 1, is known at the beginning of the period (i.e., it is not a source of uncertainty). The investor has an initial real wealth, Wt, and chooses to hold a proportion of this wealth, x, as an Australian bill with nominal return iA with the remainder (1 − x) held as a US bill with nominal return ius. Real end-of-period wealth, Wt + 1, is therefore
where, S is the spot exchange rate, S = $US/$A. Defining δ by
end-of-period wealth is given by
The investor is assumed to have a constant relative risk aversion, β, and hence seeks to maximize expected utility of the form
where consumption, c, satisfies c = Wt + 1. By construction, the only source of uncertainty arises from movements in the $US/$A exchange rate which lead to δ being a random variable. As we find evidence that changes in the $US/$A exchange rate exhibit both skewness and leptokurtosis (see section V), we consider the first four moments of the distribution of δ. Thus, expanding f(δ) = [1 + xδ]1 − β as a Taylor expansion around f(0) and including terms up to δ4, leads to an expression for expected utility, EU(x), as a function of the share of initial wealth held in Australia, x. Expected utility maximization implies that dEU(x)/dx = 0, and imposing this condition gives
This equation gives the nominal risk premium, E δ – equivalent to rp in equation (1) – which the Australian bill must pay to induce the investor to hold a proportion x of wealth in Australia, as a function of the higher moments of the distribution of δ. The coefficient of relative risk aversion, β, is thought to be about two (see, for example, Friend and Blume (1975) or Newberry and Stiglitz (1981)). Quantitative estimates of the risk premium are derived from Dataset A using the period Jan 84 to Apr 89 and assuming β = 2. As mentioned above, the period of the model is four weeks.[9] Sample estimates of the unconditional four-week moments[10] of δ are: Eδ2 = 1.27 × 10−3, Eδ3 = −1.99×10−5, and Eδ4 = 5.69×10−6. These numbers are used in equation (9) to calculate the nominal risk premium as a function of the fraction of the portfolio held in Australia and the results are displayed in Figure 4.[11]
Nominal risk premium required to hold short-term Australian bills
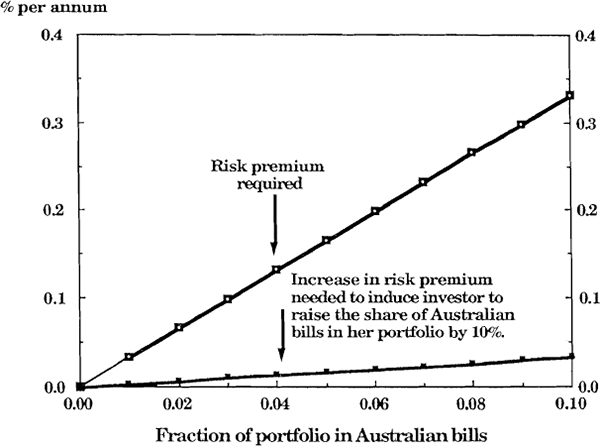
An estimate of the proportion of Australian assets held in an international asset portfolio can be derived from a survey reported in The Economist March 25, 1989. Nine international investment banks were asked for their best mix of investments (equities, bonds and ‘cash’) over the next 12 months. Their suggestions for the geographical location of their equity holdings (but not their bond or cash holdings) were reported. Of six who suggested putting part of their portfolio in Australia, the range of recommended Australian portfolio shares was 0.1% ≤ x ≤ 2.5%. When examining Figure 4, we may use these numbers as a guide to estimating portfolio shares for Australian bills.[12] For x ≤ 2.5%, the risk premium required to induce such a holding is less than 0.09% p.a., and the increase in risk premium required to induce an investor to raise Australian asset holdings by 10% is less than 0.01%p.a.
For the estimated values of the second, third and fourth moments of δ, and for values of x relevant to Australia, the effects of skewness and leptokurtosis on the risk premium are negligible – only the Eδ2 term on the rhs of equation (9) contributes to the risk premium. Truncating the analysis beyond this term is equivalent to applying mean-variance analysis. Such analysis can be conducted without some of the restrictive assumptions used above, and it forms the basis of our second simple model. Thus, we now (i) assume that the price index for the basket of goods at the end of the period, Pust + 1, is unknown at time t, and (ii) allow our investor to choose nominal assets in Australia and four other countries (Canada, Japan, U.K. and West Germany) as well as the US. Let ρj be the real return on the nominal asset from country j, defined by
where S [j/$US] is the price of currency j in US dollars (equal to one when j = US). Define ρ as the column vector of the five non-US real returns, ρj, j≠US, and z as the column vector of real returns relative to the real return on the US asset:
where τ is a column vector of five ones.[13] Define x as the column vector of the five non-US portfolio shares – and thus the share allocated to the US asset is (1 − x' τ). Finally, define Ω as the variance-covariance matrix of the real excess return of the non-US assets
where the expectation is formed at the beginning of the period under consideration. If the investor maximizes a function of the expected value and variance of her end-of-period wealth, then Frankel and Engel (1984) show that
We now use equation (10) to derive quantitative estimates of E zA, the expected excess real return on the Australian asset over the US asset, or equivalently, the real risk premium, rpR from equation (2), which a US investor requires to hold a fraction xA of her portfolio in Australian bills. The first term on the rhs of equation (10) is zero if it is assumed that the price index Pust + 1 is known at time t. Even if the price index is unknown, this term should be very small, because inflation rates are so much less volatile than exchange rates. Sample estimates of the unconditional covariances and variance needed to calculate E zA are provided in Table 3.[14] Appendix C describes how the estimates are derived.
| var (zA) | 11.9×10−4 (2.55×10−4) |
cov (zA, z£) |
3.23×10−4 (1.60×10−4) |
|---|---|---|---|
| cov (zA, ρus) | 0.249×10−4 (0.183×10−4) |
cov (zA, zDM) |
2.76×10−4 (1.76×10−4) |
| cov (zA, z¥) | 2.58×10−4 (1.58×10−4) |
cov (zA, zc) |
−0.90×10−4 (0.37×10−4) |
To estimate E zA, it is also necessary to have estimates of the portfolio share held outside the US. Remember that wealth, as defined here, is consumed at the end of the model. For the sake of realism, this wealth should include labour income, since this makes up a large proportion of average consumers' resources. Hence, for a representative consumer, we should expect that only a small proportion of wealth is available to be held as a portfolio of foreign assets.[15] As an illustrative calculation, assume that the total portfolio share held in countries other than the US or Australia is 0.10, and that this share is divided in proportion to GNP (so that x¥ = 0.053, xDM = 0.024, x£ = 0.015, xC = 0.008).[16] Substituting these numbers and the point estimates in Table 3 into equation (10), and again assuming β = 2 gives
Thus, for example, to induce our investor to hold xA = 0.01 of wealth in Australia (as well as 0.10 in other countries in the above proportions), a real return in Australia 0.16% p.a. higher than the real return in the US is required. The reader is invited to choose alternative portfolio shares, and evaluate the corresponding risk premia.
Finally, we estimate the increase in risk premium needed to induce our investor to raise the proportion of wealth held in Australia by ΔxA. It is no longer necessary to make specific assumptions about the portfolio shares held in other countries. Provided the increase in Australian holdings comes at the expense of assets held in the US, equation (10) implies
To induce the representative consumer to put an extra 0.01 (that is, 1%) of wealth in Australia, an extra average return in Australia of 0.031% p.a. is required. At the risk of appearing uncontroversial, this number seems rather small to us.
Footnotes
It would make minimal difference to construct a four-week forward rate. [7]
Thorp et. al. (1988) estimate equation (5) for market expectations of their trade-weighted $A. They find their point estimate β = 3.52 is very significantly different from β = 1, and hence they reject the null of zero risk premium. This result is dominated by their survey expectations from Nov 84 to late 85. For expectations formed from late 85 to the end of their survey in Mar 88, they accept the null of zero risk premium. Analysis of the sub-sample of our survey data from Mar to Oct 85 also reveals a statistically significant risk premium, which is not present in the sub-sample from Nov 85 to the end of the sample in Sept 87. [8]
Despite suggestions to the contrary (Juttner and Luedecke, 1988), covered interest parity seems a very good approximation for the Australian–US foreign exchange market after the float of the $A (Frankel and Froot, 1987; Smith, 1989a). We therefore use the approximation: (1 + itA)/(1 + itus) = (St/Ft, 1 month)12/13. The exponent 12/13 is used to convert from one month forward to four weeks forward. δ is therefore defined by: 1 + δ = (St + 4/St).(St/Ft, 1 month)12/13, where the subscript t is defined in weeks. Of course, almost all the variation in δ arises from the term (St + 4/St). [9]
As Pagan (1988) stresses, the risk premium at any time is determined by the moments of δ conditional on information available at that time. The unconditional moments give an estimate of the average conditional moments over some extended period of time – a few weeks or a few months (see Frankel, 1988). Appendix B addresses this issue, but it does not change the conclusions presented here. [10]
To stress the point: we do not evaluate the actual excess return on Australian bills over the sample period. Rather, we calculate the excess nominal return that a utility maximizing US investor requires because of the volatility – measured in $US – of the nominal return on her Australian asset. It is this excess return that constitutes the risk premium. We tested the sensitivity of the results to changes in some of the assumptions. Deriving the moments of δ using Dataset B, or alternatively, superimposing a constant depreciation of the $A of 10% p.a. (equivalent to 0.736% every four weeks) on the actual exchange rate data both lead to estimates of the risk premium almost identical to those shown in the Figure. [11]
As will be discussed shortly, the representative consumer is probably not free to put all her financial resources into an international asset portfolio, and hence these numbers should be overestimates. [12]
zA, the Australian element of z (zA ≡ ρA − ρus), satisfies zA ≡ δ.(1 + ius).Pust/Pust + 1, where δ is defined by equation (8). [13]
Again, it is the conditional moments which determine investor behaviour and the unconditional moments give an estimate of the average conditional moments over some extended period of time (a few weeks or a few months). See Appendix B. [14]
Consumers may not be able to make large borrowings against future labour income and/or may have substantial financial commitments (e.g., borrowing for a house) which limit their capacity to invest in foreign assets. [15]
Based on 87 GNP using average exchange rates in Dec 87. [16]
With the minor exception of Canada, if the rise in Australian holdings is at the expense of other foreign holdings, the increase in risk premium is even smaller than equation (11) because of the positive values of cov (zA, zj), j ≠ C. [17]