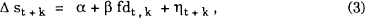RDP 8906: A Random Walk Around the $A: Expectations, Risk, Interest Rates and Consequences for External Imbalance II. Exchange Rate Expectations and the Forward Rate
October 1989
- Download the Paper 1.72MB
To begin, we define the notation to be used in the paper for spot and forward exchange rates. Let St [a/b] be the spot price of currency ‘a’ measured in currency ‘b’ at time t (so that an increase in St [a/b] represents an appreciation of currency b with respect to currency a) and let Ft,k [a/b] be the price at time t, k periods forward. Further, let lower case exchange rate variables denote the natural log of upper case exchange rate variables (st [a/b] ≡ ln St [a/b] and ft,k [a/b] ≡ ln Ft,k [a/b]).
The forward rate
A standard way to test whether the forward rate is a biased predictor of the future spot rate (see e.g., Hodrick (1987), Goodhart (1988)) is to estimate the equation
where Δ st + k = st + k − st, fdt,k = ft,k − st is the current k-period forward discount[2] and ηt + k is the error term. If the change at time t predicted by the (log) forward discount is an unbiased predictor of the actual (log) change in the spot exchange rate, then α = 0 and β = 1. By contrast, if β = 0, the forward rate (or forward discount) tells us nothing about the future movement of the spot rate. Finally, if β < 0, on average over the next k periods, the deviation from trend of the spot rate is in the opposite direction to the deviation predicted by the forward discount.
Table 1 reports regressions of equation (3) for the $A/$US market over two different time periods for both a four week and a thirteen week horizon. The reason for the two different time periods and technical details concerning the regressions are discussed in Appendix A. Details about the exchange rate dataset (dataset A) are provided in the Data Appendix. In all cases in which data from overlapping time periods are used (Table 1 is the first example), the standard errors (SE) of the estimates are evaluated using the technique of Hansen (1982).
| k (Weeks) |
Intercept |
Coefficient on Forward discount |
||||
|---|---|---|---|---|---|---|
| Coefficient | SE | Coefficient | SE | R2 | DW | |
| Four* | −0.011 | 0.009 | −1.93 | 1.59 | 0.023 | 0.40 |
| Four+ | −0.007 | 0.014 | −1.67 | 2.15 | 0.011 | 0.47 |
| Thirteen* | −0.028 | 0.016 | −0.35 | 1.22 | 0.003 | 0.12 |
| Thirteen+ | −0.039 | 0.025 | −1.20 | 1.72 | 0.022 | 0.12 |
Dataset A: * 6 Jan 84 to 21 Apr 89; + 15 Feb 85 to 21 Apr 89. |
||||||
There is by now “considerable evidence for a variety of currencies and sample periods … that indicates a strong rejection of the proposition that the forward rate is an unbiased predictor of the future spot rate” (Hodrick, 1987, p. 54). To give a recent example, Goodhart (1988) estimates equation (3) for nine datasets (using daily, weekly and monthly exchange rate data on four currencies against the $US). Six of his point estimates of β are negative and in five cases his estimate is significantly (more than two standard errors) less than 1. By contrast, none of his estimates are significantly different from 0. That is, he cannot reject the hypothesis that the forward discount has no capacity to explain future movement of the spot rate.
For Australia, Thorpe et. al. (1988) estimate equation (3) over one month, three month and six month horizons using a trade-weighted exchange rate measure (formed from bilateral exchange rates with the US, Japan, West Germany and Britain). Their period of estimation ranges from Dec 83 – Sept 87 to Nov 84 – Jan 88, and each of their point estimates of β is negative – but the level of significance is low. Only for a one month horizon can they reject H0: β = 1 at a 5% level of significance.[3] All the regressions in Table 1 are consistent with this pattern – negative point estimates of β – but again the level of significance is low. Only in the case of the first reported regression can the hypothesis H0: β = 1 be rejected at the 5% level in favour of the alternative H1: β < 1.
Survey data on exchange rate expectations
Between Mar 85 and Sept 87, The Australian newspaper published the results of a market survey of expectations of the $US/$A conducted by Dr. Ben Hunt. For almost the whole sample period sixteen of the major companies involved in the foreign exchange market took part in the survey. Every Friday between 2pm and 5pm each company's chief foreign exchange dealer was asked his/her expectation of the spot value of the $US/$A at 3pm the following Friday and at 3pm in four weeks time (see Hunt, 1987). Further details of the survey are in the data appendix. In this sub-section we analyse the four week expectational data.
Figures 1 and 2 show comparisons of the four week exchange rate expectations with the one month forward rate, the four-weekly inflation differential between the US and Australia (πust − πAt),[4] and the behaviour of the spot rate. Define set + k as the (log of the) mean of the market participants' expectations of the spot rate in k weeks,[5] and Δ set + k by Δ set + k = set + k − st. Judged by the root mean square error (RMSE) over the sample period, both the average market participants' four-week forecast (set + 4) and the forward rate (ft, 1 month) are marginally worse forecasts of the spot rate in four weeks than the no-change forecast (set + 4 ≡ st) one would use if one thought the exchange rate was a martingale or a random walk without drift. The root mean square errors are respectively, 3.3% and 3.2% compared with a RMSE for the no-change forecast of 3.1%.[6] Table 2 reports estimates of equation (3) for the time period of the expectational data as well as four other equations.
Average four week forecast, forward rate and change in spot rate for $US/$A
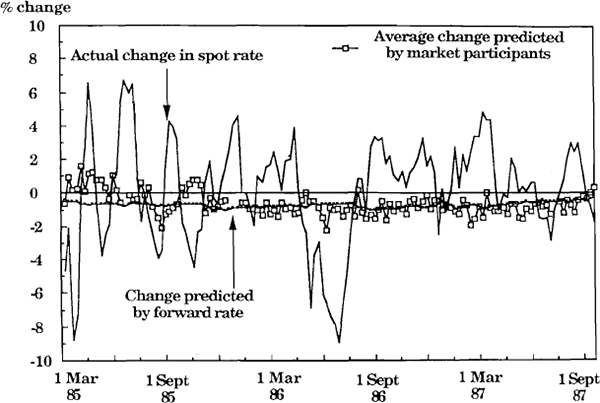
Average four week forecast compared with the forward rate and the inflation differential
| R2 | DW | ||||
|---|---|---|---|---|---|
| Equation (3) Δ st + 4 = α + β fdt, 1 month | |||||
| Estimates | −0.044 | −6.18 | 0.098 | 0.47 | |
| Standard errors (SE) | (0.023) | (3.11) | |||
| Equation (4) Δ st + 4 = α + β fdt, 1 month + γ (πust − πAt) | |||||
| Estimates | −0.044 | −6.22 | 0.10 | 0.098 | 0.47 |
| SE | (0.024) | (3.24) | (3.16) | ||
| Equation (5) Δ set + 4 = α + β fdt, 1 month | |||||
| Estimates | 0.002 | 1.20 | 0.071 | 0.96 | |
| SE | (0.005) | (0.69) | |||
| Equation (6) Δ set + 4 = α + β fdt, 1 month + γ (πust − πAt) | |||||
| Estimates | 0.0065 | 0.514 | 2.10 | 0.309 | 1.25 |
| SE | (0.0040) | (0.547) | (0.53) | ||
| Equation (7) set + 4 − st + 4 = α + β fdt, 1 month | |||||
| Estimates | 0.047 | 7.38 | 0.131 | 0.47 | |
| SE | (0.023) | (3.14) | |||
Survey and exchange rate data: Weekly (Fridays), 8 Mar 85 to 18 Sept 87. |
|||||
Estimation of equation (3) over the period of the exchange rate surveys again shows a negative point estimate of β (Table 2). The hypothesis H0: β = 1 is rejected at the 5% level in favour of the alternative H1: β < 1. Equation (5) shows that, on its own, the forward rate has significant explanatory power for the average exchange rate change expected by market participants. On the basis of estimates of this equation for their (fairly extensive) survey expectations data, Froot and Frankel (1989) conclude that “expectations seem to move very strongly with the forward rate”, although they don't examine alternative explanators for expectations. The evidence from equation (6) is that our survey expectations seem to move strongly with the inflation differential rather than the forward rate. Importantly, this is in stark contrast with the actual exchange rate which shows no tendency to move in the direction predicted by either the forward discount or the inflation differential either over the sample period (equation 4) or during the whole period of the $A float (not shown). Equations (3) and (5) can be combined to give equation (7) which demonstrates that the average expectational error at time t exhibits statistically significant correlation with information available to the market at time t (the one month forward discount at t). This is evidence that either market expectations are not rational, or that over this period, the $A/$US market suffered from a ‘peso problem’. These possibilities are examined in the discussion section.
Over the sample, the average annual inflation differential between Australia and the US was 5.4% p.a., the average annual rate of depreciation implied by the one month forward rate was 8.2% p.a., while market participants expected depreciation at an average rate of 7.8% p.a. On average, the actual rate appreciated at 2.7% p.a. Corresponding figures for the period Nov 85 – Sept 87 were 6.5% p.a. for the inflation differential, 8.5% p.a. for the one month forward rate, 10.5% p.a. for the average market participant compared to an average rate of appreciation of the actual rate of 2.8% p.a.
Thorpe et. al. (1988) report an extensive survey of market participants' exchange rate expectations at a one month horizon. The surveys were conducted weekly from Nov 84 to Mar 88 and used to estimate expectations of a trade-weighted $A exchange rate (TWA, to distinguish it from the Reserve Bank's TWI). Their study shows interesting similarities with our survey results. They fit equation (7) for their expectations data and conclude, as we do, that the average expectational error at time t is correlated with the forward discount at t. From Nov 84 to Dec 85, their market participants expected nominal appreciation of their TWA at an average rate of 4.7% p.a. This seems to correspond quite well with our expectations results for most of 1985 (see Figure 2). From Jan 86 to the end of their sample in Mar 88, their participants expected nominal depreciation of their TWA at an average rate of 8.6% p.a. – again somewhat comparable to our results.
An objection to the use of survey data to draw inferences about market expectations is this: “Consider the incentive problem of a trader who possesses private information that he has used to construct a portfolio of positions based on the deviations of his expectations from the current forward rates. When [someone] calls him for his expectations, will he reveal his information, or will he lie and quote something like the forward rate? Does he even know that the two are different?” (Hodrick, 1987 p. 135) Two points are worth making in response to this objection. Firstly, Goodhart (1988) provides evidence that foreign exchange traders – and the banks they work for – very seldom take open positions over a period as long as a month, which suggests that if traders have private information they very rarely think it sufficiently reliable to use it in the marketplace. Secondly, it is easy to understand the nature of private information in, for example, the stockmarket. In that market, there are obvious examples of potentially private information likely to affect a company's future profitability (e.g., the discovery of a valuable mineral ore deposit) and hence its stock price. But what is the nature of private information which, on average, helps to predict the value of the $US/$A exchange rate in four weeks time? If such information exists, it has been kept secret from macroeconomists for some time. Our best models of exchange rate determination over a four-week (or substantially longer) horizon do not perform significantly better than a random walk forecast (Meese and Rogoff, 1983). This second point sounds flippant, but is meant in all seriousness.
Footnotes
Given our definitions of s and f, if for example st is the log $US/$A rate and fdt,k is positive, then in the forward market the $US is trading at a discount compared to the spot market. [2]
For this regression, they also reject β = 0 at a 5% level of significance. [3]
To derive inflation, we use price indices which had been published when the expectations were formed. Australian quarterly CPI numbers were always published by the end of the month immediately following the end of each quarter. For each Friday in month i we therefore define annual Australian inflation as Pi − 4/Pi − 16 − 1, where Pi is the CPI for the quarter containing month i. For these numbers, we adjust for the ‘Medicare effect’ – which affects the estimates for the first twenty one weeks. Defining pi as the monthly CPI for the US, annual US inflation is defined as pi − 3/Pi − 15 − 1. Four weekly inflation is derived from these annual inflation figures. [4]
Much existing literature imagines that there is a single expectation that is homogeneously held by investors. We assume that this expectation is being measured by the mean of the responses. One can take the somewhat more sophisticated view that we measure the ‘true investor expectation’ with a measurement error (Froot and Frankel, 1989). Our econometric tests remain valid provided this measurement error is random (and hence uncorrelated with information available when the expectation is formed). [5]
This result tallies with others who find that over a short horizon, market participants' forecasts of the future exchange rate are often worse, but never significantly better than a ‘no-change forecast’ – Lowe and Trevor (1986), Hunt (1987) and Manzur (1988). [6]