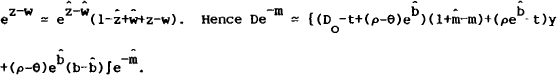RDP 8611: The Effectiveness of Fiscal Policy in an Economy with Anticipatory Wage Contracts 2. The Underlying Model

(a) Private Sector Behaviour

Let output be produced by identical firms employing constant capital and variable labour with a constant returns to scale production function. “Effective capital” is assumed to grow at the labour force growth rate, n, and in a steady state, output per capita is constant. Effective capital per capita is normalised to unity; since steady state output per capita depends only on this magnitude, it also must be unity. Firms are assumed to be are able to sell all their output. Defining the logarithm of output per capita as y and of real wages as w, profit maximisation conditional on the real wage gives output as a negative function of the real wage or

where c_O is a constant, and ρ is the share of profits in output. The Walrasian steady state value of the logarithm of output, 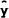, is 0, and so the steady state output gap is defined to be y.

Output may be greater than its steady state (or natural) rate, if the real wage falls below . Firms can attract labour beyond the natural rate (say, in the form of overtime), although such an occurrence is only temporary because the real wage will subsequently be bid upwards.

Perfect indexation of wages to goods prices is assumed. Representative wage-setters make periodical nominal wage contracts, suffering two costs: a fixed cost per contract; and a cost over the life of the contract if the indexed wage deviates from that associated with the system in a full employment steady state. This means that the latter cost will be provoked if actual (expected) inflation differs from steady state inflation (over the life of the contract); as the gap between these increases, so the real wage will be bid down. In aggregate, the rate of change in real wages depends upon the output gap and upon the inflation gap, 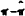. In the Appendix the following equation is derived

where w(o) = w_o. Perfect indexation implies that discrete jumps in the price level are always matched by nominal wage jumps – hence the real wage is predetermined. The existence of 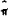, or, what has been called “core Inflation” (see Buiter and Miller (1982)) in the above Phillips curve is a critical element for the results in this paper. If η' were 0, then output would only depend upon the predetermined real wage, and there would no further interest in the inflation-output tradeoff. The parameter, ϕ', which measures the sensitivity of wage change to unemployed resources is shown in the Appendix to depend on the inflation gap; this aspect is ignored at minor cost in all but the final section.

Differentiating (1) and substituting into (2) gives the equation which will drive output

where

If inflation is currently above its steady state level (and expected to eventually regress to that level), then nominal wages will rise at a slower rate than inflation and output will be stimulated. With output set by firms facing predetermined real wages, aggregate demand management only has a bearing insofar as it can influence the inflation gap and hence the real wage.

Output is sold to households and to government. No investment is permitted. The share of government expenditure in output is given at a point in time, and so the goods market equilibrium condition effectively solves for household expenditure. The price level adjusts instantaneously to ensure that this condition is met. Alternatively, and equivalently in this model, the price level will maintain continuous equilibrium in the money market.

Households own shares in the “effective capital” of firms. With effective capital per capita normalised to unity, the real rate of return, r, is defined by profits, which varies with output, i.e. r=ρe^Y. Linearising about the steady state, where 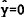gives

A market and a price for capital is excluded deliberately to retain algebraic manageability of the model. It may be acceptable to think of the shares as being instantaneous, short term assets that mature instantly and are re-issued.

In Section 4, real short term government debt is introduced into the model. The rate of interest on this debt will be equalised to the rate of return on effective capital. The real rate of interest is seen to be positively related to output in (4).

Households also hold real money balances, defined in logarithms as m. The stock of nominal money balances is predetermined at a point in time by past issues by the government. The price level is free to adjust instantaneously to enable aggregate households to reach their desired real money balances. Assuming perfect foresight of inflation the demand for real money balances depends negatively on the nominal interest rate, r+π, and positively on output.

When m^d=m is imposed in Sections 3 and 4, we can generally describe money market equilibrium by (using (4))

where 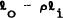is normalised to 0 and 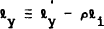is assumed positive

A useful definition for this paper is the inflation or interest elasticity of the demand for money, ξ

(b) The Government's Budget Constraint

The first model to be analysed (in Section 3) excludes government debt and assumes that the per capita fiscal deficit, D_o, can only be financed by issuing money. Linearised^[4] in logarithms, about the steady state, this means that

In the steady state, 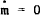and the deficit is financed by inflation taxes

The inflation tax is composed from a tax rate, 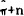, and a tax base, 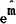. As inflation increases, the rate rises at the expense of the base. The tax initially rises reaching a maximum when the inflation elasticity of demand for money reaches unity. Thus the maximum sustainable deficit, 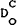, is obtained at the point when ξ reaches unity, or, from (6) and (8), at the critical steady state inflation rate.

Using (8) in (7) gives

In this simple model, there is no need to distinguish between fiscal and monetary policy makers. Domination of one over the other is irrelevant.

The second model (of Section 4) includes real or indexed short term government^[5] debt, b, as another means of financing the deficit. To proceed, we now have to introduce assumptions about the relationship between the fiscal and monetary authorities. The fiscal deficit will be assumed to comprise endogenous and exogenous elements. The endogenous elements arise in part because government spending and taxation vary with output. The extent to which they vary may be a contributor to the stability of the equilibrium of the system. The issue of debt implies higher debt service costs in the future and therefore further issues. This potentially destabilising force can be mitigated if the issue of debt can raise output and reduce the deficit. However, if steady state debt must rise, taxes on steady state output will be irrelevant for ensuring the stability and existence of this equilibrium.

The fiscal authorities will be obliged to introduce fiscal rules which respond to the level of outstanding debt. The total deficit, D, inclusive of debt service is given by

Remembering that y and b are in logarithms, t and θ represent the linearly endogenous elements of fiscal policy.

This total deficit has to be financed by money and debt. Just as with fiscal policy, monetary policy shall be endogenous, except for an extreme parameter value. That parameter is α which gives the share of the deficit financed by money. If α = 0 monetary growth may be exogenously set at a non-zero value. The effectiveness of fiscal policy will be seen to depend upon its dominance over monetary policy – α>0. Hence αD is financed by the real per capita value of nominal money issue, and (1−α)D by per capita real debt issue

In steady state, 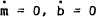and

where, noting that 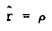from (4)

Linearising^[6] (10) about the steady state, using (12)–14), gives

Similarly linearising (11) about the steady state gives

From (11)', there appears to be no problem about stability of debt issue. Indeed the partial derivative of 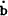with respect to b is simply −n. This is mere appearance. The process of expressing the model in logarithms has implicitly enforced the assumption that

The existence of the steady state in (13) and (14) requires positive (D_o−t)/n+(1−α)(θ−ρ) because e^b cannot be negative. Assuming net deficits, D_o−t>0, in steady states, (15) is a necessary condition for existence.

A sufficient condition is that θ>ρ. If a government seeks to ensure that its fiscal deficit improves more than the steady state debt service worsens, then that government will be called FISCALLY CAUTIOUS. If it utilises the freedom conferred by growth and sets θ so that it lies between ρ and 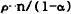, it will not be considered cautious.

The inflation tax finances a policy-determined share of the deficit, D_o−t. From (13)–(14), that share is given by 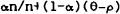. The inflation tax is maximised where ξ is unity, and so the critical inflation rate remains (9). The maximum sustainable exogenous deficit, 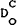, with money and debt financing will be greater than in the case of just money financing because the inflation tax ceiling only restrains that portion of the deficit financed by money. 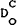will also be greater as θ and t, the endogenous components of fiscal policy, increase.

Footnotes

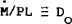Writing nominal money balances (not in logarithms) as M, population as L and prices as P, the budget constraint is or 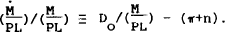This can be written in terms of m as

View MathML

which can be linearised using a Taylor's expansion on 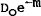, i.e.

View MathML

[4]

The use of real rather than nominal debt is an unimportant assumption. All the results in the paper go through. An additional source for the base of the inflation tax would be obtained with nominal debt. [5]

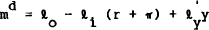
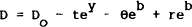
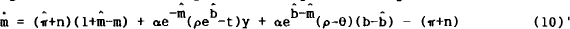
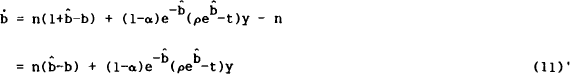
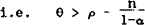
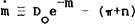
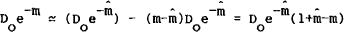
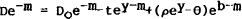The linearisation of utilises the approximation

View MathML

[6]