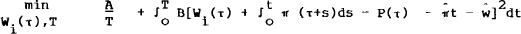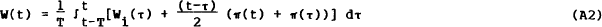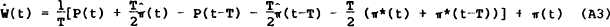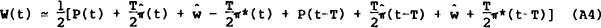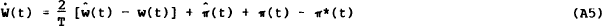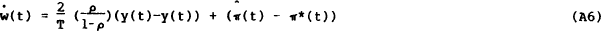RDP 8611: The Effectiveness of Fiscal Policy in an Economy with Anticipatory Wage Contracts Appendix

To establish the wage adjustment equation (2), I shall adapt the analysis described in Mussa (1981). A representative wage setter incurs a fixed cost, A, for each T-length contract that it makes. Over the life of the nominal wage contract, prices are rationally expected to change. There are two inflation concepts that are relevant – current inflation and the equilibrium inflation. In this paper the latter is interpreted as state inflation, . Assume that the nominal wage is perfectly indexed to current price movements both discrete and continuous. After having build indexation into the nominal wage, the individual wage setter is assumed to suffer a quadratic cost over the life of the contract which depends upon the difference between the indexed nominal wage, deflated by the expected price if it were inflating at , and the full employment real wage, 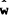. Recognising that the frequency of adjustment is 1/T, the problem of the ith agent is

Approximating the indexation integral assuming near linearity in time, 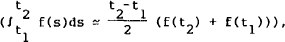the solutions for the optimal wage before inflation indexing and the optimal contract length are

where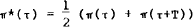

The optimal wage after indexing makes a mid-point correction for the change in core prices. The optimal contract length is seen to decrease with the inflation gap, since the cost of incorrect real wages are increased. As steady state is approached, the frequency of recontracting declines towards zero; in steady state, there is no need to renegotiate in finite time, indexation being sufficient. The endogenous contract length phenomenon is ignored in the dynamic analysis; basically, it stretches out the convergence process, by slowing adjustment speeds.

To aggregate, assume all wage setters to be identical, their indexed wages equispaced over the unit interval and ordered by the date of the most recent wage bargain. This gives the aggregate nominal wage after indexation as

Inserting (A1) in (A2), differentiating with respect to t, and making the approximation 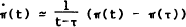gives

Assuming near linearity in time of the integral in (A2), the aggregate nominal wage approximates as

A(3) and A(4) together with the fact that w(t) = W(t) − p(t), imply

or, using (1), that

Equation (2) in the text is derived from (A5) on the assumption that 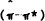is always some fraction of 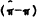. The contract length inflation gap will always be smaller than the steady state gap.