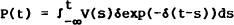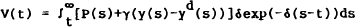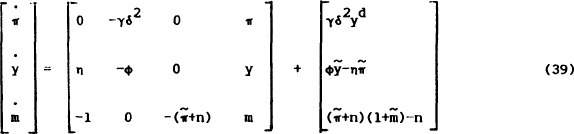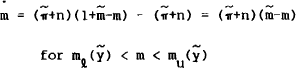RDP 8611: The Effectiveness of Fiscal Policy in an Economy with Anticipatory Wage Contracts 5. Stickiness in Goods Prices

In the previous two sections, expansionary fiscal policy could have beneficial output effects in an economy with sticky real wages but flexible prices. If goods prices were also sluggish the dynamic version of the fix-price macroeconomic models would be applicable.

One generalisation disaggregates the goods market into a flexible price and a sluggish price sector. As the share of the flexible price sector declines, the results of the previous two sections would be moderated. The reason is that current inflation would become increasingly restrained in its excessive short run response to unanticipated fiscal shocks. In the limit, there would never be an inflation gap to exploit. This diminution of the supply-side effectiveness of fiscal policy would occur provided the economy remains in a regime where firms determine output and employment. In the fix-price modelling terminology, a Classical Unemployment (CU) regime would have to exist.

A necessary (but not sufficient) condition for CU is that the real wage exceeds its Walrasian steady state value 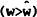implying 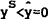, where y^S is output supply. In addition, to support CU for given 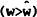, the Walrasian steady state gap of the price level cannot be (a) greater by an amount that would reduce real money balances below a floor denoted 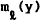beyond which aggregate goods demand would be below supply creating Keynesian Unemployment (KU), or (b) less than an amount that would raise real money balances above a ceiling m_u(y) and reduce labour supply below demand, creating Repressed Inflation (see Barro and Grossman (1976)). CU will be assumed henceforth.

While traditional fiscal effectiveness results apply in a KU regime, they do not apply in a CU one; excess goods demand would be exacerbated by a fiscal expansion, simply adding to inflation with no feedback. To establish this, I shall use the Calvo (1983) model of price sluggishness, incorporating the possibility of steady state inflation.

Goods price contracts are stochastic and exponentially distributed, identically and independently, over the range of products. Any existing contract at t will last till t+τ with probability δ exp(−δτ). Aggregating over contracts that fixed a price, V(s) at a previous date δ, the current (predetermined) price level becomes

which is equivalent to

If CU steady state inflation is non-zero, 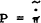, the (marginal) steady state contract price, 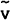, exceeds the aggregate price, 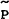, by the amount 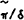, where 1/δ is the expected duration of the contract. The CU steady state (denoted by ‘~’) may or may not be identical to the Walrasian steady state.

By assumption, the contract price rationally accounts for future aggregate prices and for the deviation of aggregate output from perceived aggregate demand y−y^d. Perceived demand^[9] is not necessarily realised because, in CU it is always greater than or equal to supply. Except in full Walrasian equilibrium, it does not equal 0. Hence

which differentiated becomes

In steady state, 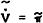, and y−y^d = 0. (36) and (37) can be combined to give

As current output rises, (for given V_t and 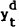) the change in contract prices falls according to −γδ. This causes a subsequent (δ) fall in inflation change. However, it is important to observe that both π and V are not historically predetermined, while P is.

Adding (38) to the simple model with just money finance^[10] described in Section 2, we get the following system.

where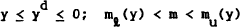

The determinant of the transition matrix is 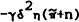and the trace is 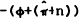. With only two predetermined variables, y and m, the sign of the determinant implies one or three negative (real parts of the) eigenvalues. Since 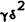is relatively small, one would expect the latter. Hence a multiplicity of convergent solutions are possible. Since any value of π may be chosen, it is standard to posit that π (and hence V) jumps immediately to its steady state value. An expected fiscal expansion will raise 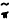and π by the same amount, and so will have no real effects.

This scenario involves a further insidious property. Since current and steady state inflation are always equal, output change is actually zero – in (3), the inflation gap is zero, but also ϕ' is zero. The Appendix demonstrates that the endogenous contract length, T, becomes infinite if there is no inflation gap and that ϕ' is inversely related to T. Real wages are only bidden down if an inflation gap exists.

Thus output is stuck below full employment and by (38) we have a CU steady state displaying full inertia

Outside the CU steady state, real money balances need not be constant. The analogue of (7)' in this section becomes

and so real balance eventually converge to 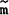where, typically 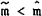. A continued rise in fiscal inflation will eventually push the system into a KU regime after real money balances fall below .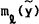

The remedy in this underemployment equilibria is the standard Classical prescription – an enforced cut in the real product wage. An alternative solution (but more difficult than the model suggests) would be to engineer a fall in real money balances (via open market operations) so that the condition in the goods market switched from excess demand to supply; Keynesian fiscal demand management could then be used. Of course, if wage indexation was abandoned, the sticky real wage problem would disappear and convergence to the Walrasian equilibrium would return.

Footnotes

Throughout this paper, the specification of aggregate goods demand has been avoided. Perceived aggregate demand will typically depend on real money balances, inflation, real wages and the fiscal deficit. [9]

The general conclusions are not altered if debt finance is permitted. [10]