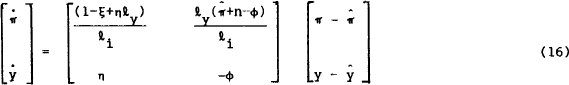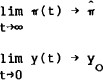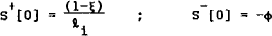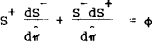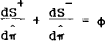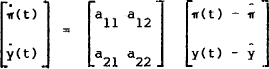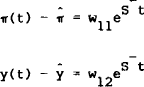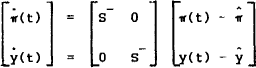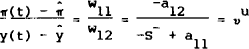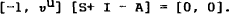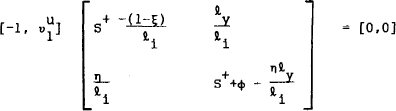RDP 8611: The Effectiveness of Fiscal Policy in an Economy with Anticipatory Wage Contracts 3. A Model of Money Finance and Flexible Prices
August 1986
This model is basically the Cagan model (see Sargent and Wallace (1973)) with endogenous output and is completely specified by (3), (5) and (7′). Prices are flexible and their changes perfectly foreseen. By Walras Law, we are entitled to drop one market; in this paper, the goods market is not specified and hence the distinction between government expenditure and taxes is irrelevant. Real money balances are not predetermined because the price level is free to jump to ensure continuous money market equilibrium. Equivalently, given the assumption of perfect foresight about inflation, the equilibrium inflation rate is also determined in this market. Output is predetermined because the nominal wage is assumed to be perfectly indexed to discrete and continuous changes in the price level.
The linear dependence between m, y and π is evident in equation (5). Any two of these three can be chosen to describe the fundamental dynamics. I analyse the model in terms of inflation and output. Using (6) one can express inflation changes as
Using (3), (7′) and (15), and introducing the definition of ξ from (6) gives the following system expressed as deviations from steady state:
It is necessary to add two boundary conditions to (16) to permit a solution. With y predetermined and π not, the conditions for a two point boundary value solution are:
I shall consider the properties of the model when initial output is in steady state (i.e. zero) and when it is in depressed (i.e. less than zero).
This type of problem is extremely well-known (see Buiter (1983) for a general statement) and it is a well accepted procedure to seek the unique convergent saddlepath solution. Without the first boundary condition, there are typically infinite possible solutions, termed speculative bubbles, where the jump variable (π in our case) takes on any value but that required to reach the saddlepath solution. One can justify the obsession with saddlepath solutions on the basis of underlying preferences if the asset involved is essential. An asset is essential if disutility becomes infinitely large as the value of the asset declines to zero. Speculative hyperinflations were ruled out by Brock (1974) on this basis. If the essential property cannot be accepted, Obstfeld and Rogoff (1984) show that a believable government guaranteed floor on an asset's value will prevent bubbles. Hyperdeflations can immediately be ruled out because eventually the real value of the asset must eventually exceed output, an impossible outcome under perfect foresight.
To find the saddlepath, we first have to establish whether one exists. In our two equation system, it is necessary and sufficient that the real parts of the two eigenvalues of the transition matrix in (16) be opposite to sign. One must be positive, the “unstable” eigenvalue S+, and the other negative, the stable eigenvalue S−. In general, one must have as many stable eigenvalues as predetermined variables. The product of the eigenvalues must equal the determinant of the transition matrix. The determinant of the matrix in (16) is
and we need it to be negative. If η=0, then a necessary condition is that ξ<1. It is too strong if η>0. This is worth noting because it is a common feature of inflation tax models that the inflation elasticity of money demand must be less than unity; this means that an increase in inflation will raise the overall tax take. If output is responsive to inflation, (η>0), then the higher output will raise money demand and hence the tax base. The direct inflation effect on the tax may then be negative, if the indirect effect via output is big enough to more than compensate. The indirect effect can also be boosted further if one allows the deficit to move anticyclically; this channel will be present in the next model. From (9), the maximum sustainable deficit is achieved as ξ approaches unity from below. Henceforth it shall be assumed that ξ ≤ 1, in which case the saddlepath condition, Δ<0, must be met.
Another property is that the sum of the eigenvalues equals the trace of the transition matrix. For the matrix in (15), we have
If η=0, the transition matrix becomes triangular and the eigenvalues, S+ and S− are immediately available from the diagonal. With obvious notation we get
For η>0, it is apparent from (16) and (18) that Δ[η] > Δ[0] and Trace [η] > Trace [0]
Since S+ = (Trace + (Trace2 − 4Δ)1/2)/2, it is simple to show that ds+/dη>0.
Hence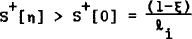 
.
This result will be very useful at a later stage. We shall need to know that
In our linear differential equation system, the saddlepath implies a unique linear
convergent relationship between the output gap, y(t), and the inflation gap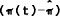 
. To be in
that relationship, the non-predetermined variable, π, is available to jump appropriately
after any shock. A restriction associated with the boundary condition has to be applied to the
general solution if we are to confine ourselves to the saddlepath. The restriction is
that we have to rule out that part of the general solution which involves the unstable
eigenvalue S+. Associated with any eigenvalue is a normalised row eigenvector, ν'
such that
where A is the transition matrix. For unanticipated shocks, the restriction to rule out the unstable eigenvalue involves the unstable eigenvector, νu in the following way.[7]
To determine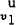 
, we solve (20)[8] to give (21) at t=0.
whose sign simply depends upon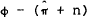 
. Thus inflation and output will be
positively correlated over time if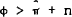 
.
The parameter ϕ measures the responsiveness of real wages to unemployed resources. If this responsiveness is low, and the underlying core inflation is high, then stagflation (or its converse) will be experienced whereby rising unemployment will be associated with rising inflation. The switch to the stagflation mode occurs at core rates of inflation that exceed ϕ−n. This was observed in many industrialised countries in the 1970's – average inflation rates were at a historical high and underlying growth, n, was falling.
The reason for this condition on ϕ is simple. If per capita output is languishing below 0,
it must rise in the future if the system is convergent. But future rising output
and current low output impacts on the direction of change of inflation,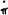 
, through
(15). Money demand will be rising with output in the future, and hence 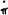can be
positive. But the inflation tax base will current be low due to output, causing the supply of
real money balances to increase thus reducing 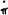. The greater is
ϕ, the faster will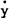 
grow and the greater 
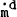; the
greater is the inflation tax rate,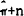 
, the greater is 
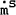. If the
former exceeds the latter, 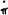will be positive, and because the
saddlepath is a line,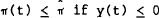 
.
Given y(0)−yo and π(0) from (21), the evolution of π and y over time, is described by
One can easily consider fiscal policy changes using the solutions in (21)' and (23). A fiscal expansion (an increase in Do) leads to a steady state increase in inflation and a decrease in real money balances if the interest elasticity of money demand is less than one. From (5), (6) and (8) we get
If the policy were instituted in a period of full employment,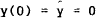 
, it
can be seen from (21) that π(0) would equal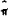 
; the inflation rate
would merely jump to the new steady state level. Nominal wages would follow suit exactly, and
there would be no need for output to move at all.
The interesting question to ask concerns the transitory relationship between inflation and
output after a supply shock. For example, if energy were a factor of production, an oil
price increase would constitute a negative supply shock that would require a fall in real wages.
Assuming the shock to have taken place sometime back, and that real wages are not yet down by
enough, output would be below potential, y(0) < 0. For a given fiscal deficit, the post-shock
level of steady state inflation would be higher than the pre-shock level (see (5) and (8)). With
sticky real wages the current inflation rate will have overshot the steady state value if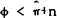 
.
The final matter of interest in this simple model is whether fiscal policy can play any role in
helping the economy out of the transitory recession of output. There is, of course, no direct
demand management role, because the output gap has been posed as a real wage or supply-side
problem. The only way fiscal policy can work is by influencing the inflation gap and thereby
real wages. From (3),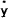 
will be greater if 
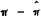can be raised. Fiscal expansion does raise steady state inflation, but with output below steady
state, it is not immediately obvious how it will affect .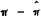
I can show that fiscal expansion will speed up output adjustment, up to a point, whether or not there is stagflation. Beyond this point, the saddlepath property of the model disappears, and both eigenvalues become negative. Since the model is then convergent from any starting point (of π and y), and not just on the saddlepath line, it is sensible to conjecture that the rate of inflation will immediately collapse to its steady state value; only ϕ will then matter for output adjustment. However, the point at which the saddlepath disappears turns out to be beyond the maximum sustainable deficit, defined where the inflation elasticity is unity.
To prove the above, one only need to know what happens to the eigenvalues, when Do,
and thus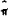
(see (24)), is increased. Remembering that ξ depends on 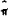, the
total differentiation of Δ (see (17)), which equals S+.S−,
gives
Differentiating the trace of the matrix in (16) gives
and so the solutions are
Now only the stable eigenvalue, S−, is relevant for the solution to y in the saddlepath zone (see (23)); since it increases in absolute size (given S+>0) fiscal pump-priming is an effective mechanism. But the positive, unstable eigenvalue also decreases eventually reaching a critical point after which it changes sign. That point is where S+ = 0 and Δ = 0 or from (17) where
Comparing (27) to (9), it is evident that the saddlepath disappears after the point of the maximum sustainable deficit.
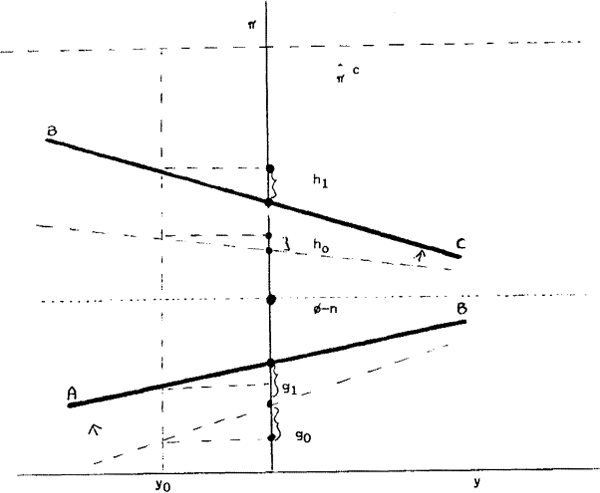
In Figure 1, the relationship between π, y, 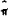and
|S−| is shown. Between points A and B,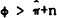 
, and the
non-stagflation case is observed. At B, ϕ = π+n and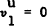 
, (see
(22)); inflation will have no influence on output. Between B and C, stagflation appears with
inflation above its steady state but set to fall as output improves. In Figure 1a, the two
possible saddlepaths (from (22)) are shown as BC and AB. A fiscal expansion shifts and tilts
them, causing the inflation gap to increase i.e. g1<go, h1>ho.
The intuitive reason why π increases more than in either zone is
that the increased nominal demand coming from the fiscal expansion can be cleared only by a
change in inflation in the short run, but over time will be eliminated by adjustment in both
output and inflation. In the stagflation zone, BC, fiscal pump-priming or declines in the
underlying population and capital augmenting growth rate, n, must eventually engender a collapse
of the system.
Footnotes
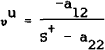which is a solution which would emerge from
[7]
