RDP 2020-01: Credit Spreads, Monetary Policy and the Price Puzzle 3. The Cash Rate Response to Credit Market Conditions
January 2020
- Download the Paper 460KB
I first show that the cash rate systematically responds to changing credit and money market conditions. This addresses one of the two requirements for biased estimates by the RR approach discussed in the previous section. However, I will also show that it implies that the RR ‘shocks’ used by BT are anticipated as financial market participants understand and expect the Bank's response to financial market conditions. This adds a second, separate source of potential bias relating to the issue of non-fundamentalness when using these shocks as instruments for monetary policy shocks in SVARs (Leeper et al 2013; Ramey 2016).
3.1 A Taylor Rule Augmented with Credit Spreads
To quantify the response of the cash rate to credit and money market conditions, I follow RR and BT and estimate a standard forward-looking Taylor-type rule in differences augmented by credit spreads:
Here denotes the change in the cash rate at the Board meeting in month t, crt – 1 its level prior to the meeting, contains the Bank's h-quarter-ahead macroeconomic forecasts provided to the Board, and CSt includes one or more indicators from a set of money or credit market spreads or other financial market indicators available at the time of the meeting. The residual, , from this regression will then serve as the RR monetary policy shock.
While other specifications of the monetary policy reaction function are conceivable, I follow the exact specification of BT to allow direct comparison of my results with their findings.[13] Accordingly, includes the two-quarter-ahead forecasts for inflation , real GDP growth , the revisions to these forecasts since the previous forecast round , and the nowcast for the unemployment rate .[14] I estimate these policy rules on quarterly data over the inflation-targeting period from 1994:Q1 to 2018:Q4 using only Board meetings for which new forecasts are available.[15]
3.1.1 Measures of credit market conditions
I augment this benchmark rule using several measures capturing risk premia in money and credit markets and financial market uncertainty. As discussed in the previous section, these measures served as important real-time gauges for financial market stress during the GFC and informed monetary policy to a considerable extent. This has also motivated their extensive use in the literature to study the effect of credit supply shocks and interbank market disruptions on real economic activity.[16] For the United States, Caldara and Herbst (2019) have used the spread between the BAA corporate and 10-year Treasury bond yields to explore the role of credit market shocks for the identification of monetary policy shocks. Following this approach for Australia is unfortunately not possible as corporate bond spreads are only available from around 2004.
Thus, I use the alternative measures of credit risk and uncertainty shown in Figure 4. First, I also use the US BAA corporate to 10-year US Treasury bond yield spread and the US VIX to capture global risk aversion and credit supply shocks on US short-term debt funding markets that are important to Australian banks. As shown by Finlay and Jääskelä (2014) and Eickmeier and Ng (2015), US credit market shocks have strong spillover effects on Australian credit markets. Second, to capture changes to domestic credit market conditions, I use two measures of money market and lending rate spreads. The spread between the 3-month bank-accepted bill (BAB) rate and the 3-month Australian dollar overnight indexed swap (OIS) rate captures credit risk on the interbank market. However, the OIS rate is also only available from July 2001. For the earlier sample starting in 1994, I hence use the 3-month risk-free zero-coupon yield as estimated by Finlay and Olivan (2012) as the risk-free benchmark. Following Finlay and Jääskelä (2014), I further use the spread between the average large business variable lending rate and its reference rate, the 3-month BAB rate .[17] As expected, these spreads are strongly correlated with the Australian BBB corporate to 10-year Australian government bond yield spread over the common sample with a correlation of around 0.5 in levels and of 0.3 and 0.45 in differences. I account for the real-time availability of all financial market information by using the end-of-month value for the month prior to the Board meeting.
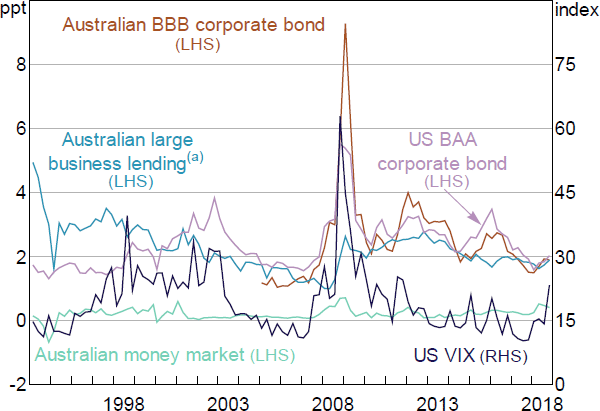
Notes:
As available at the beginning of forecast months (end-quarter months to 2000, mid-quarter months since); see Figure 2 for further notes
(a) Spread between Australian large business variable lending rate and 3-month bank bill rate
Sources: Author's calculations; Federal Reserve Bank of St. Louis; RBA
3.1.2 Estimation results
Similarly to the findings of Caldara and Herbst (2019) for the United States, I find a strong and economically significant response of the policy rate to credit market conditions (Table 1). On average, the Board aims to offset a bit more than half of any exogenous change to money market spreads ( , regression BT-CS1). The cash rate response to business lending spreads , US credit spreads and financial market uncertainty is also significant (regressions BT-CS2 to BT-CS4, respectively), similar to findings for the United States in Evans et al (2015) and Caggiano et al (2018). On average, a 100 basis point increase in the spread between business lending and the benchmark money market rate is met by a 18 basis point cut to the cash rate (regression BT-CS2). I also find that each of the three credit spread measures provides additional, unique information to the Board (regression BT-CS). While the estimated coefficients on domestic business lending spreads and the US corporate bond spread decline, they remain statistically significant at the 10 per cent level. The US VIX does not add additional information as soon as the US corporate bond spread is accounted for (not shown).
The responses to domestic money market and credit market spreads are not only statistically significant but also economically meaningful. Compared to the BT benchmark specification without any credit or money market spreads, my preferred specification (BT-CS) doubles the explanatory power of the model and now accounts for more than half of the total variation in cash rate changes. However, this does not result from materially changed responses to the Bank's forecasts. Similar to BT, I find that the Board reacts most strongly to revisions to the inflation and output forecasts .
| Variable | BT | BT-CS1 | BT-CS2 | BT-CS3 | BT-CS4 | BT-CS |
|---|---|---|---|---|---|---|
| Constant | −0.25 | 0.20 | −0.30* | 0.15 | −0.08 | 0.30* |
| ctt – 1 | 0.00 | 0.01 | −0.01 | 0.02 | 0.01 | −0.01 |
| 0.02 | −0.02 | −0.02 | −0.02 | −0.01 | 0.00 | |
| 0.08*** | 0.03 | 0.08*** | 0.04 | 0.05* | 0.02 | |
| −0.01 | −0.02 | 0.06** | −0.02 | −0.01 | 0.00 | |
| 0.21*** | 0.19*** | 0.16** | 0.16** | 0.22*** | 0.15** | |
| 0.07** | 0.06** | 0.08** | 0.07** | 0.08** | 0.07** | |
| −0.71*** | −0.60*** | |||||
| −0.18*** | −0.08* | |||||
| −0.18*** | −0.06* | |||||
| −0.01** | ||||||
| Observations | 100 | 100 | 100 | 100 | 100 | 100 |
| R 2 | 0.280 | 0.525 | 0.370 | 0.381 | 0.329 | 0.574 |
| Adjusted R 2 | 0.234 | 0.489*** | 0.322*** | 0.334*** | 0.278* | 0.532*** |
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively; for variable definitions and their sources, see Appendix C; statistical significance of the difference in model fit (Adjusted R 2) to the benchmark is assessed using a likelihood ratio test | ||||||
3.2 Is the Response to Credit Market Conditions Anticipated by Financial Markets?
The strong and consistent response of the cash rate to money and credit market risk spreads suggests that considerable profits could be made by predicting the Bank's response to money and credit market conditions, unless financial market participants are already aware of this systematic response. Inferring that this is not the case suggests that cash rate changes, even after accounting for the Bank's forecasts, are anticipated by financial market participants. As a result, the RR shocks used by BT would not qualify as valid instruments for true, unanticipated policy shocks and may give rise to the issue of non-fundamentalness when using them as instruments for shocks in a SVAR.
I address this question by adding financial market participants' expectations about the change in the cash rate over the next quarter to the RR regression in Equation (15).[18] After adding these expectations to the BT benchmark rule and the policy rule augmented by credit spreads (regressions BT and BT-CS of Table 1), all other coefficients in both policy rules are now close to zero and insignificant (Table 2, regressions BT-EXP and BT-CS-EXP). Only the coefficient on the expected cash rate is significant and positive as expected. This suggests that the Bank's policy reaction function – including the response to financial market conditions – is well understood and anticipated.[19]
| Variable | BT | BT-EXP | BT-CS | BT-CS-EXP |
|---|---|---|---|---|
| Constant | −0.25 | −0.04 | 0.30* | 0.02 |
| crt – 1 | 0.00 | 0.01 | −0.01 | 0.01 |
| 0.02 | 0.03 | 0.00 | 0.01 | |
| 0.08*** | 0.02 | 0.02 | −0.01 | |
| −0.01 | 0.00 | 0.00 | −0.02 | |
| 0.21*** | 0.04 | 0.15** | 0.03 | |
| 0.07** | 0.04* | 0.07** | 0.03 | |
| −0.60*** | 0.11 | |||
| −0.08* | 0.06* | |||
| −0.06* | −0.03 | |||
| 0.53*** | 0.59*** | |||
| Observations | 100 | 100 | 100 | 100 |
| R 2 | 0.280 | 0.763 | 0.574 | 0.773 |
| Adjusted R 2 | 0.234 | 0.753*** | 0.532 | 0.761*** |
| Notes: See notes for Table 1; statistical significance of the difference in model fit is assessed against either the BT or BT-CS benchmark model excluding cash rate expectations | ||||
These findings thus suggest that the residual obtained from the BT regression not only includes a systematic response to credit market conditions but is also predictable using financial markets' expectations about future cash rate changes. This can further be seen by regressing this residual on the expected cash rate change prior to the Board meeting:
I find that expected cash rate changes explain around half of the variation in the residuals from the original Bishop and Tulip (2017) regression and predict these residuals with a slope coefficient of 0.29 (Figure 5; Table 3). In contrast, expected cash rate changes explain only around 10 per cent of the variation in the residuals from the augmented BT-CS regression. However, the positive and significant relationship between expected cash rate changes and both the BT and the BT-CS residuals questions their suitability as shocks reflecting a structural disturbance (Ramey 2016; Stock and Watson 2018).[20] I will thus purge the residuals from the augmented model (BT-CS) of this additional anticipatory component when constructing the monetary policy shock series in Section 5.
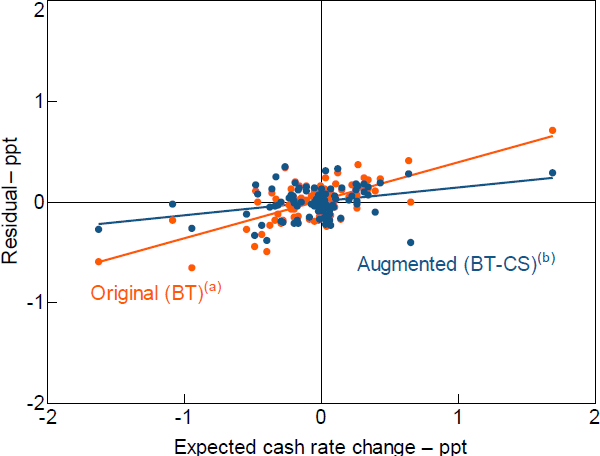
Notes:
Lines of best fit from Equation (16)
(a) Residuals from regression BT of Table 1
(b) Residuals from regression BT-CS of Table 1
| Variable | BT | BT-CS |
|---|---|---|
| Constant | 0.02 | 0.01 |
| 0.29*** | 0.12*** | |
| Observations | 100 | 100 |
| R 2 | 0.473 | 0.134 |
| Notes: Dependent variables are residuals from regressions BT and BT-CS of Table 1; see Table 1 for further notes | ||
Footnote
All subsequent results are robust to changes to this specification as discussed in Appendix D. [13]
The Bank arguably targets inflation at much longer horizons than two quarters. But the Bank's longer-term forecasts for inflation and economic activity are conditional on an assumed or predicted path of the cash rate and hence include feedback effects from the policy decision. This motivates the use of forecasts for short horizons. At these horizons, any immediate cash rate changes are unlikely to have material effects on inflation and economic activity. At the same time, inflation and output are strongly serially correlated, so that short-term forecasts should provide a good approximation of longer-term forecasts (Romer and Romer 2004). [14]
The Reserve Bank Board meets on the first Tuesday of every month except January (11 times per year) to set the cash rate. For four of these meetings, the Bank staff updates all forecasts. I only use cash rate changes for these forecast months (end-quarter months prior to 2000 and mid-quarter months since) to estimate the policy reaction function (Equation (15)). BT show that using cash rate changes for all meetings and using internal staff forecasts or forecasts from Consensus Economics does not resolve the price puzzle. The forecasts used are updated from BT and are forecasts as published in the SMP a few days after the Board meeting. BT show that changes to the forecasts after the meeting are usually trivially small, and do not correlate with either cash rate increases or decreases. [15]
Using these indicators, the literature has explored the role of credit supply shocks originating from shifts in risk sentiment of investors for the business cycle (e.g. López-Salido et al 2017), and found these indicators have strong predictive power for future economic activity (e.g. Gilchrist and Zakrajšek 2012). [16]
I further explored spreads between small and large business lending rates, and the variable mortgage to cash rate spread but found no response of the cash rate to these spreads over and above the Bank's forecasts and the other spread measures. [17]
I obtain these expectations from the zero-coupon yield curve estimated by Finlay and Olivan (2012). I use the cash rate change as expected on the last day of the month preceding the Board meeting to align this measure with the credit spread measures. [18]
It may also suggest that policy changes are communicated in advance. While the Bank occasionally communicates its outlook on the likely direction of future cash rate changes, it does not publish a forecast for the cash rate path nor has it engaged in direct forward guidance. This explanation is hence less likely to explain this finding. [19]
In contrast to Ramey (2016) and Miranda-Agrippino and Ricco (2018) I find no evidence for serial autocorrelation in any of the shock series. [20]