RDP 2020-01: Credit Spreads, Monetary Policy and the Price Puzzle 2. Biased Romer and Romer Estimates – The Role of Credit Spreads
January 2020
- Download the Paper 460KB
To establish the arguments and mechanisms in this paper more clearly, I replicate a simple model of the economy from BT to outline how anticipatory monetary policy by an inflation-targeting central bank may bias our estimates of the effect of monetary policy on inflation, how the RR approach aims to address this, and under which conditions the RR approach fails to remove this bias.
2.1 Anticipatory Monetary Policy and the Price Puzzle
Assume inflation is determined as follows
and assume for simplicity that the cash rate affects inflation only through the observable determinant(s) of inflation Xt (e.g. unemployment or output as captured by a standard VAR model),
Here, is the rate of inflation in period t, rt is the cash rate announced in t, Zt – 1 is a variable (or vector of variables) that helps the central bank predict inflation but that is unobserved (or otherwise omitted from the model) by the econometrician, and and are unforecastable white noise innovations. The researcher then aims to estimate by running the simple regression:
The estimator is given by[7]
which will suffer from omitted variable bias if: (i) (the central bank responds to indicators not observed by the econometrician), and (ii) (these indicators have predictive information for inflation over and above what is captured in the researcher's model, here Xt – 1).[8]
Both conditions are likely satisfied. Central banks monitor a wider range of macroeconomic or financial indicators than included in a small-scale VAR. As a consequence, following Sims (1992), the literature typically adds additional ‘information’ variables such as commodity prices to the simple, small-scale monetary policy VAR models to better capture the central bank's forecasts. Commodity prices are posited to have additional predictive content for inflation , and as a result the central bank raises the policy rate in response . If , then and the price puzzle emerges. However, as shown by Hanson (2004), the additional predictive content of these variables in Zt – the basis on which they are included – is weak at best, and adding additional variables does not necessarily resolve the price puzzle.
But the Bank monitors a wider range of indicators than just commodity prices and also obtains unique information through its business liaison program. This vast amount of information helps the Bank predict inflation to an extent that alternative forecasts or simple models used by researchers usually cannot (Tulip and Wallace 2012). As evident from the Board minutes, this information also guides the Board's cash rate decisions. However, adding this broad range of indicators to the VAR model is not feasible without applying some dimension reduction technique.[9]
RR thus aims to remove the anticipatory component in policy rate changes by controlling directly for the central bank's (inflation) forecasts . A potential concern is that the central bank's forecasts take into account any planned changes to the cash rate. This motivates the use of short-term forecasts by RR and BT, given the likely longer lag with which the cash rate affects inflation and the high persistence of inflation. Assume for now that the forecast is produced by weighing information from Xt and Zt and under the assumption of a constant cash rate (or no feedback from the cash rate to the forecast). Following BT, I formalise this by assuming that Xt enters the forecast with a lag:
In the first step, the researcher estimates:
In the second step, the residual is then used as a proxy for the true monetary policy shock mt to estimate the effect of a cash rate change on inflation using a simple univariate regression[10]
The estimator of is then
which is unbiased because as the residual is orthogonal to the unobserved predictor Zt – 1 by controlling for the central bank's forecasts Ft – 1 at the time the cash rate was set.
2.2 Bias in the Romer and Romer Approach
The RR approach should be able to successfully remove any anticipatory component of monetary policy with respect to its inflation objective as long as the Bank's forecasts reflect all information that the Board's cash rate decision is based on. Importantly, the approach does not require the Board to only change the cash rate in response to the Bank's inflation forecast. If the Board changes the cash rate for reasons other than achieving its inflation target, these changes can be used as instruments for policy shocks with regard to inflation. The approach only requires that cash rate changes made in anticipation of inflation outcomes are based on the inflation forecast alone, and not on any other information.
These insights can be used to highlight how the RR approach may fail to remove the anticipatory component of monetary policy. The following assumptions may feel hypothetical for now, but I will argue later that they hold. Assume that Zt is a determinant of inflation as before (see Equation (1)), but it does not inform the Bank's central inflation forecast, that is
The cash rate still affects inflation only through Xt as before. While the Bank's forecasts do not incorporate the information in Zt, the Board nonetheless responds to this information, that is
This may reflect the fact that the Board views Zt as informative about the risks around the central forecast, and therefore responds to this information, or that the Board forms their own forecasts based on the central forecast produced by the Bank and the information contained in Zt.
Following the RR approach, the researcher omits this additional response to Zt when estimating
Accordingly, the obtained instrument for the policy shock is correlated with the information and another, plausibly exogenous shock in Zt thus violating the exogeneity condition of being a valid instrument for the true, unobservable policy shock mt (see, for example, Stock and Watson (2018) for a discussion). The first-stage estimator of is then given by
and is unbiased as long as the Bank's central forecast does not incorporate information from Zt, that is, . The researcher then estimates the effect of a cash rate change on inflation as
The estimator is given by
which is biased if (Zt is a determinant of inflation beyond what is captured in the central bank's forecasts through Xt) and (the cash rate responds to Zt over and above the central bank's forecasts).[11]
I will show that both of these conditions are likely fulfilled with Zt including credit risk spreads in money market or lending rates. The cash rate systematically responds to such spreads over and above the Bank's forecasts, and these spreads explain the Bank's forecast errors for inflation and the unemployment rate. Since the Board lowers the cash rate when credit spreads rise and higher spreads are associated with lower inflation than forecast , the bias will be positive . If the price puzzle emerges.
2.3 Narrative Evidence around the GFC
For an inflation-targeting central bank to adjust its policy rate but not its forecasts in response to information that has predictive content for inflation may appear surprising at first. But going back to the GFC episode may offer some support for this and provide some intuition for how it may lead to the emergence of the price puzzle found by BT.
During the GFC, the Bank paid particular attention to a wide range of financial market indicators. These indicators signalled in real time the sharp deterioration in financial market conditions around September 2008. This deterioration was driven by uncertainty about the passage of the Troubled Asset Relief Program (TARP) in the United States, the exposure of financial investors and intermediaries to the asset-backed securities market and the quality of the assets underpinning those securities (Debelle 2018). As a result, risk premia on money and fixed income markets rose sharply, reflecting increased risk aversion, greater uncertainty and liquidity hording of financial intermediaries and investors. Indicators such as spreads between corporate and government bond yields, money market risk premia and stock market volatility indices thus provided real-time signals about the stress on global financial markets at the time (Figure 2).
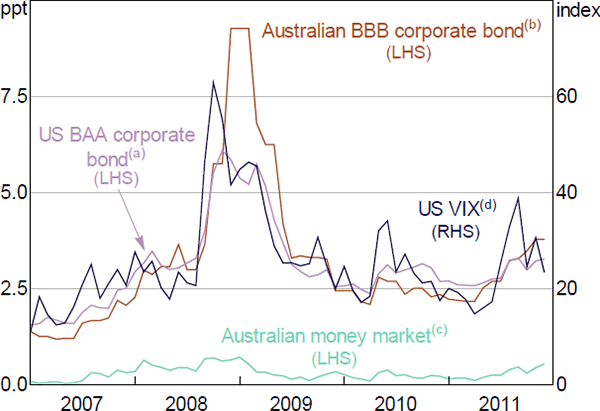
Notes:
(a) US BAA corporate to 10-year US Treasury bond yield
(b) Australian BBB corporate bond rate to 10-year Australian government bond yield
(c) Australian 3-month bank bill rate to zero-coupon yield
(d) Chicago Board Options Exchange, CBOE Volatility Index
Sources: Author's calculations; Federal Reserve Bank of St. Louis; RBA
The Reserve Bank Board responded decisively to this deterioration in global financial market conditions and cut the cash rate by a total of 275 basis points from October to December 2008. However, these cuts were not accompanied by marked changes to the forecasts. While the inflation forecasts remained largely unchanged over this period, the unemployment rate forecasts were revised upwards only in early 2009 after the cash rate had already been reduced by 300 basis points from its August 2008 level (Figure 3).
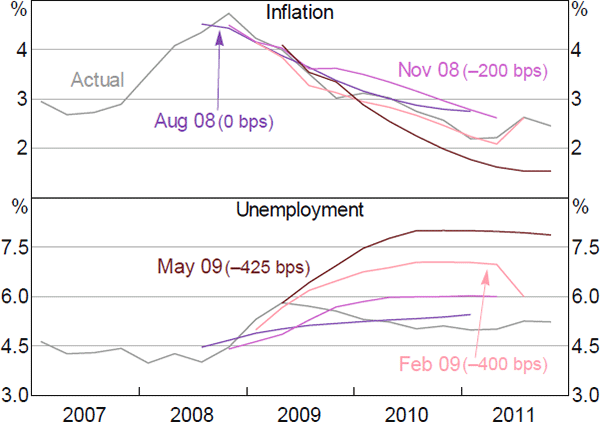
Notes: Forecasts of underlying inflation (year-ended) and the unemployment rate as published in the Statement on Monetary Policy (SMP ); cumulative cash rate changes since June 2008 in parentheses
Sources: ABS; Author's calculations; RBA
So why were the cash rate and the Bank's forecasts adjusted differentially in early 2009? The minutes of the Board meetings reveal that the sharp reductions in the cash rate over the last three months of 2008 were primarily a response to the sharply worsening conditions in international financial markets, the deterioration of the global outlook and the resulting increased downside risks for domestic growth and inflation (RBA 2008a, 2008b, 2008c). These developments were obviously not only observed by the Board but by the Bank's staff, too. Informing the Board's views, the Bank immediately lowered its outlook for output growth and raised its longer-term unemployment rate forecast in November 2008 (RBA 2008d). In contrast, the inflation forecast was initially revised upwards on the back of a strong depreciation of the exchange rate. However, the duration and extent of the global financial market turmoil and the weakness in global growth and its spillovers to the Australian economy were unclear at the time, especially given that most real economic indicators held up until around early 2009 (RBA 2009). Accordingly, the Bank staff did not centralise the information from financial market indicators into its forecasts, but assessed that they presented considerable downside risks to the outlook (RBA 2008d).[12]
For a researcher following the RR approach, the sharp reduction in the cash rate would hence appear as a large accommodative monetary policy shock given the lack of forecast adjustments. And as inflation eventually printed lower than forecast by the Bank, this decline in inflation would thus be attributed to the ‘surprise’ easing of monetary policy, thereby supporting a positive correlation between monetary policy changes and future inflation. As an isolated incident, this would unlikely be able to explain the price puzzle. But if this relationship was systematic, the policy shocks previously identified by BT would in fact be a mix of cash rate changes exogenous to the economic outlook and a systematic, endogenous response to changes in credit market conditions.
Footnotes
See Appendix B for further derivations of the estimators. [7]
Another source of bias may be that the cash rate affects inflation through Zt, that is, . Gilchrist and Zakrajšek (2012) and Caldara and Herbst (2019) show that credit market conditions are an important transmission channel for monetary policy. Modelling this channel explicitly does not change my results as shown Section 6.1. [8]
One approach to condense the information of a broad range of indicators is to estimate ‘factors’ that capture common signals from the set of indicators and add these factors to the VAR model (Bernanke, Boivin and Eliasz 2005). Hartigan and Morley (2018) find that this resolves the price puzzle for Australia. However, the factor model assumes that the Bank's forecasts are obtained by linearly combining all observable information. Furthermore, the factor model cannot observe ‘soft’ information (e.g. information obtained through liaison) and additional staff judgement. [9]
I will use the term ‘shock’ going forward. However, the purged cash rate change may be endogenous to other (short-term) objectives of the Bank. Thus, it may be better thought of as an ‘instrument’ for the part of a cash rate change that is exogenous with regard to the central bank's inflation and growth outlooks rather than a ‘structural disturbance’ in a fully specified model (Ramey 2016). The obtained policy shocks do not have to be, and are not necessarily, exogenous to the Bank's outlook for other variables. [10]
An alternative explanation could be that the Bank's staff anticipated the strong cash rate response to offset any effects of the GFC on inflation and unemployment even in the short to medium term. This is unlikely given the typically assumed long lags with which a cash rate change would affect real economic activity and inflation. [12]