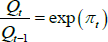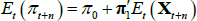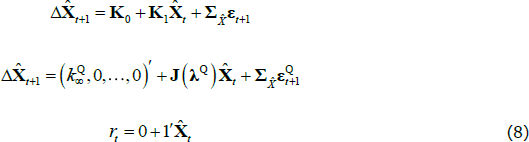RDP 2018-02: Affine Endeavour: Estimating a Joint Model of the Nominal and Real Term Structures of Interest Rates in Australia 2. The Model
February 2018
- Download the Paper 1,673KB
We start by outlining the model that we will use in this paper. It is a joint model of the nominal and real term structures of interest rates. As has been well documented in the literature (e.g. JSZ; Guimarães 2016), there are a number of difficulties associated with the estimation of ATSMs, namely: small-sample problems, and numerical and computational issues. We address the first by incorporating survey data into the estimation, and address the latter by employing a generalised version of the JSZ normalisation. Below we discuss exactly how these are incorporated into the model. We work in discrete time throughout. For a more detailed treatment and derivation of the model, see Appendix A.
2.1 Deriving a Joint Affine Term Structure Model
The basic structure of ATSMs is relatively simple. These models assume that there are underlying (latent or observable) ‘pricing’ factors that drive both observable economic variables, such as the short-term interest rate or the inflation rate, and also risk preferences via a so-called ‘price of risk’. They are called affine models because they imply that observable bond yields are linear functions of these factors.
2.1.1 An ATSM of nominal interest rates
Considering first an ATSM of nominal interest rates, we assume that the one-period nominal interest rate (rt) is given by
where ρ0 is a scalar and ρ1 is a vector, so that rt is a linear function of the N pricing factors Xt. Moreover, we assume that the data-generating process (also called the ‘real-world distribution’ or ‘P dynamics’) of these pricing factors is a vector autoregressive (VAR) process with one lag
where μ is an N × 1 vector of intercepts, θ is an N × N matrix describing the evolution of Xt, and the N error terms εt + 1 ~N(0,IN).[3] Combining Equations (1) and (2) shows that the evolution of the short-term rate is controlled by the P dynamics.
As investors are risk averse, the price that they are willing to pay for a bond depends both on the expected level of interest rates over the life of the bond (governed by Equations (1) and (2)) and the risk that owning a bond entails, relative to rolling funds in short-dated securities. Following Duffee (2002), we assume that the market price of risk is also a linear function of the factors and is given by
where λt is an N × 1 vector that represents the price of risk associated with each of the factors at time t, λ0 is an N × 1 vector and λ1 is an N × N matrix. The specification implies that for each factor i, the compensation demanded by investors for bearing the risk associated with that factor is a constant λ0,i plus a linear combination of all the factors.
The market price of risk in turn determines the term premium, which is the compensation that investors receive/pay for locking in an interest rate for a long period, rather than rolling over short-dated securities. As discussed in Cochrane (2001), the size and sign of this premium will depend on two things:
- The amount of risk in the economy (i.e. the volatility/uncertainty around the future path of interest rates and the level of consumption).
- The covariance between bond returns and agents' marginal utility of consumption in different states of the world. That is, whether the bond provides a hedge for consumption risk or adds to consumption risk. If the bond is expected to provide relatively high returns during bad economic times when consumption is low and the marginal utility of additional consumption is high, then the bond provides a hedge to agents' consumption risk. In this case, owning bonds is similar to owning insurance against bad states of the world. Similar to normal insurance contracts, agents will be willing to pay extra for this hedge and so the bond yield, which is inversely related to its price, will be below the average interest rate expected to prevail over the life of the bond, resulting in a negative term premium. If, on the other hand, the bond is expected to fall in value during bad economic times, then it adds to investors' risk and investors will demand a higher yield, and therefore pay a lower price, resulting in a positive term premium.[4]
If we impose a no-arbitrage condition and assume a particular functional form for how agents price risk (called the ‘stochastic discount factor’), Equations (1) to (3) imply a set of pricing equations for zero-coupon nominal bond yields. In particular,
where 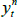 is the yield at time t for an n-period zero-coupon nominal bond (i.e. a bond that matures in n periods), and An and Bn are functions of the underlying model parameters (see Appendix A for further details). Of note, these bond pricing equations turn out to be equivalent to what would be obtained by assuming that investors were risk neutral (so λ0 = 0 and λ1 = 0) but that the pricing factors followed some other risk-adjusted (or risk-neutral) dynamics, often referred to as the ‘Q dynamics’
is the yield at time t for an n-period zero-coupon nominal bond (i.e. a bond that matures in n periods), and An and Bn are functions of the underlying model parameters (see Appendix A for further details). Of note, these bond pricing equations turn out to be equivalent to what would be obtained by assuming that investors were risk neutral (so λ0 = 0 and λ1 = 0) but that the pricing factors followed some other risk-adjusted (or risk-neutral) dynamics, often referred to as the ‘Q dynamics’
for 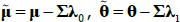 and
and 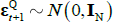 . In the literature μ and θ are often referred to as ‘P parameters’ as they determine the real-world or P dynamics, while
. In the literature μ and θ are often referred to as ‘P parameters’ as they determine the real-world or P dynamics, while 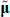 and
and 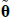 , or equivalently, λ0 and λ1, are referred to as ‘Q parameters’.
, or equivalently, λ0 and λ1, are referred to as ‘Q parameters’.
2.1.2 An ATSM of real interest rates
Real zero-coupon bonds pay one unit of consumption good at time t + n, or Qt + n/Qt units of nominal value, where Qt is the price level at time t. This is in contrast to nominal zero-coupon bonds, which pay one unit of nominal income at time t + n.
We define the one-period inflation rate πt as
and, similar to the one-period nominal interest rate, assume it to be linear in the factors
Using the same assumptions as above (i.e. those regarding the P dynamics, the nominal rates, the price of risk, the functional form of the stochastic discount factor and the lack of arbitrage opportunities) leads to a similar set of pricing equations for real zero-coupon bonds, where
for 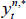 the real yield at time t for an n-period zero-coupon inflation-indexed bond, and
the real yield at time t for an n-period zero-coupon inflation-indexed bond, and 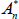 and
and 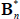 functions of the underlying model parameters (including those for inflation).
functions of the underlying model parameters (including those for inflation).
2.1.3 Incorporating surveys
As noted above, the bond pricing equations are the same in the case where investors are risk neutral and the pricing factors follow the Q dynamics, and the case where investors are risk averse, but the pricing factors follow the ‘true’ P dynamics. In practical terms, this means that the cross-section of bond yields only identifies the Q dynamics. To separate out the P dynamics we have to rely on the time series of interest rates, which follow the true P dynamics.
The difficulty is that interest rates tend to be very persistent, and so even an apparently long sample (25 years) may only contain a small number of interest rate cycles, and only a small amount of information on the P dynamics. As such, ATSMs tend to be subject to small-sample problems.
For example, Bauer, Rudebusch and Wu (2012) note that the first step of the JSZ estimation procedure (discussed in more detail below) involves estimating a VAR on the observed pricing factors, which, having been constructed from the yield data, are highly persistent. VARs estimated using highly persistent series tend to produce downwardly biased estimates of the persistence of the series in small samples. As such, the approach will tend to underestimate the persistence of the observable factors and therefore produce estimates of long-term expected interest rates that are too stable.[5]
Two approaches have been suggested to address these small-sample issues. The first is to use statistical small-sample adjustments, such as bootstrapping, as proposed by Bauer et al (2012). The second is to incorporate surveys, as in Kim and Orphanides (2012). Guimarães (2016) argues that, as the issue fundamentally relates to a lack of information, the solution is to add more information on the P dynamics, and that this can be achieved by incorporating surveys as they provide additional cross-sections of expected future rates.[6] We follow the latter approach and incorporate survey data on interest rate and inflation expectations, which we treat as unbiased but noisy readings on the underlying quantities.[7] This can be done relatively easily. For example, the expected one-period inflation rate in n periods' time is given by
which can be solved in terms of the model parameters by iterating forward using Equation (2); see Appendix B.
2.2 The JSZ Normalisation
The ATSM described above is not identified unless we apply some normalisations. For intuition, consider a model that matches a set of observed yields and survey expectations. If we were to multiply the pricing factors and appropriate model parameters by negative one, the model would still fit the observables, but the parameters and pricing factors would be different.
Many papers follow Dai and Singleton (2000) in normalising the volatility matrix. This creates a strong link between the P and Q parameters because the volatility matrix appears in both the P and Q dynamics (Equations (2) and (5)), leading to an ill-behaved likelihood surface (i.e. one with multiple local maxima and flat areas), and therefore to computational difficulties, as these models are estimated by numerically maximising the likelihood function.
JSZ propose a different normalisation that largely breaks the link between the P and Q parameters, leading to a better-behaved likelihood function.[8] In particular, JSZ note that the nominal ATSM outlined above is observationally equivalent to another ATSM with a transformed state variable 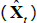 that can be summarised as
that can be summarised as
where 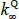 is a scalar, J(λQ) is a diagonal matrix,
is a scalar, J(λQ) is a diagonal matrix, 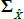 is a lower triangular matrix and 1′ is a vector of ones. Moreover, JSZ show that if the original pricing factors (Xt) are taken to be some linear combination of the yields, such as the principal components, the normalisation delivers a complete bifurcation of the likelihoods of the P and Q dynamics. In this case one can estimate the P parameters by estimating a VAR on the observed factors using ordinary least squares (OLS). The remaining Q parameters can then be estimated by maximising the likelihood over the observed yields, conditional on the previously estimated P parameters. This significantly cuts down on the number of model parameters that must be estimated by numerical optimisation, and so makes estimation faster and more stable.
is a lower triangular matrix and 1′ is a vector of ones. Moreover, JSZ show that if the original pricing factors (Xt) are taken to be some linear combination of the yields, such as the principal components, the normalisation delivers a complete bifurcation of the likelihoods of the P and Q dynamics. In this case one can estimate the P parameters by estimating a VAR on the observed factors using ordinary least squares (OLS). The remaining Q parameters can then be estimated by maximising the likelihood over the observed yields, conditional on the previously estimated P parameters. This significantly cuts down on the number of model parameters that must be estimated by numerical optimisation, and so makes estimation faster and more stable.
Extending this approach to account for real bonds is relatively simple. With the transformed state variable, the equation for inflation becomes
where the mapping between the parameters in Equations (6) and (9) is the same as the mapping between those in Equations (1) and (8). As such, we can simply add the recursive pricing equation for the real bonds to the Q optimisation and maximise the likelihood of the observed nominal and real yields, conditional on the P dynamics.
Footnotes
Guimarães (2016) also estimates a joint model using an extension of the JSZ approach, although fewer details are given and this is not the main focus of the paper. [2]
The relatively restrictive error assumption used here, and throughout the paper, is unlikely to hold in the data. While we could allow for more complex error structures, doing so would significantly increase the complexity of the model. Moreover, Bibkov and Chernov (2011) find that doing so helps models match higher-order moments of the data, but not the first moments (i.e. yields). [3]
An example of government bonds providing a form of insurance is the global financial crisis, which saw bond yields fall (and therefore bond prices rise) amid deteriorating economic circumstances. An example of the opposite is the 1970s, when relatively poor economic outcomes were accompanied by rising yields. [4]
Expected inflation and interest rates at long horizons are driven by the expected value, under the P dynamics, of the pricing factors. If the pricing factors mean-revert quickly under P dynamics, these values will simply converge to a constant. [5]
One potential concern with this approach is that the expectations of bond traders could differ from the expectations of survey participants. However, the literature tends to find that the two sets of expectations are consistent with each other (e.g. Chernov and Mueller 2012). [6]
We experimented with bootstrapping, but the estimated forward rates a number of years ahead appeared unreasonably volatile. [7]
For more details, see Appendix B. [8]