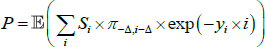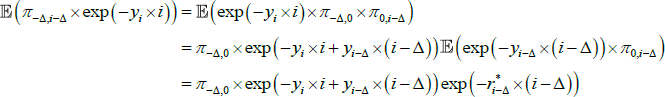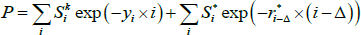RDP 2018-02: Affine Endeavour: Estimating a Joint Model of the Nominal and Real Term Structures of Interest Rates in Australia Appendix C: Estimating the Real Zero-coupon Yield Curve
February 2018
- Download the Paper 1,673KB
Unlike nominal bonds, there are relatively few inflation-indexed bonds on issue for the majority of our sample period, which makes estimating a zero-coupon real yield curve difficult. In particular, between 1992 and 2011 there are between two and three inflation-indexed bonds with residual maturity between 1 and 15 years outstanding at any one time, while from 2012 there are four to five such bonds outstanding at any one time. This low number makes fitting a flexible yield curve problematic, as arbitrary choices in yield curve modelling can have a non-negligible impact on the estimated curve shape.
To alleviate this problem we choose a particularly simple and transparent yield curve fitting method: interpolating the forward rate between outstanding bonds. So, for example, if the shortest-to-maturity inflation-indexed bond has two years until maturity and a yield of 1 per cent, we set the forward rate out to two years at 1 per cent. We then calculate what forward rate is required to price the next bond on the yield curve correctly, taking into account the previously estimated forward rates, continuing until all bonds are priced. This delivers estimated zero-coupon forward and yield curves that minimise spurious ‘wiggles’ and that price all outstanding bonds correctly.
For the ATSM we only use yield data for tenors where we have an outstanding bond, and do not use yield data interpolated between bond maturities, which further minimises the effect of the zero-coupon yield curve estimation on our final results.
In addition, we adjust the estimated zero-coupon real yield curve for the effects of known, lagged inflation on bond prices. The observed price, and so yield, of inflation-indexed bonds depends on past inflation a little. In particular, the cash flows of an inflation-indexed bond are determined by realised inflation ending two quarters before the quarter of the cash flow (so if the bond pays a coupon in November – that is, the December quarter – then the payout is based on inflation up until the end of the June quarter). Similarly, the bond price formula linking quoted real yields to bond prices in dollar terms depends on a cumulative inflation factor that is updated daily but is predictable up to a quarter and a bit in advance, with the degree of predictability determined by where in the quarter one is. This predictability will be incorporated into market prices and so will distort observed real yields: for example, a high inflation read will boost the nominal value of a real bond (since the bond's payouts will be boosted by the high inflation read once the pricing formula fully updates), and so will tend to push down the observed real yield relative to a ‘true’ real yield based on only forward-looking expectations. We correct for this by pushing the real yield back up a bit.
Consider an inflation-indexed bond paying real coupons Si at time i (where the final face value payment is included in the Si), let P be the price of this bond today, let πa,b be the cumulative inflation between a and b, where time is measured relative to today, let yi be the nominal yield, and let 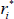 be the unobserved ‘true’ real yield that would be observed if inflation-indexed bonds did not suffer from indexation lag. We will recover
be the unobserved ‘true’ real yield that would be observed if inflation-indexed bonds did not suffer from indexation lag. We will recover 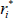 by writing the observed bond price P as a function of known inflation and nominal yields, and the unknown true real yield, and solving for the latter. In particular, by summing up nominal cash flows we can write
by writing the observed bond price P as a function of known inflation and nominal yields, and the unknown true real yield, and solving for the latter. In particular, by summing up nominal cash flows we can write
where the first two terms in the sum on the right give the nominal value of the real coupons after adjusting for cumulated inflation, and the third term is the nominal discount factor, where Δ is the indexation lag. Now for i ≤ Δ, π− Δ,i − Δ is known and we write 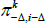 to distinguish this. For i > Δ,
to distinguish this. For i > Δ,
where the last line follows from expressing the real yield in terms of the expected value of cumulated inflation discounted by a nominal yield. As such, letting 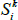 represent coupons that are currently known and
represent coupons that are currently known and 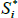 represent coupons that depend on future inflation, we can write the inflation-indexed bond price P as
represent coupons that depend on future inflation, we can write the inflation-indexed bond price P as
where 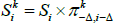 for those coupons where inflation is known, and we define
for those coupons where inflation is known, and we define 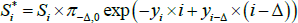 for those coupons that depend on future unknown inflation (as well as some lagged inflation). As the yi can be estimated from nominal yield curve data,
for those coupons that depend on future unknown inflation (as well as some lagged inflation). As the yi can be estimated from nominal yield curve data, 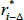 is the only unknown quantity above and we can solve for it numerically; differences between the observed real yield and the ‘true’ real yield that we estimate will be driven by (i) observed inflation via π−Δ,0, and (ii) the level and slope of the nominal yield curve via yi.
is the only unknown quantity above and we can solve for it numerically; differences between the observed real yield and the ‘true’ real yield that we estimate will be driven by (i) observed inflation via π−Δ,0, and (ii) the level and slope of the nominal yield curve via yi.
In practice, the inflation-indexed bond pricing formula linking quoted real yields to actual bond prices is updated with half the increase in the past two quarters' CPI reads, so as well as knowing one or two pricing formula updates perfectly in advance, we also know an additional ‘half’ of a pricing formula update. We treat the case as we do for the known formula updates (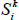 above), but in this case the π−Δ,i − Δ factor is half known and half solved for in estimation, with the unknown inflation component taken as the relevant nominal yield less the fitted real yield, using the identity that nominal = real + inflation.
above), but in this case the π−Δ,i − Δ factor is half known and half solved for in estimation, with the unknown inflation component taken as the relevant nominal yield less the fitted real yield, using the identity that nominal = real + inflation.