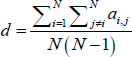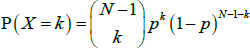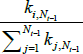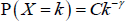RDP 2018-01: A Density-based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market 3. The Network Structure of the IBOC Market
February 2018
- Download the Paper 1,628KB
Studying the IBOC market as a ‘network’ allows us to better understand how the banks are related and the importance of each bank to the proper functioning of the market. It is well known that certain network structures are more prone to disruption than others. For example, shocks are more likely to propagate through highly connected networks, but the effect on each part of the network may be small (Allen and Gale 2000). Conversely, in weakly connected networks, the effect of most shocks will be localised, but a small number of highly connected banks could make the system fragile to shocks hitting one of these banks (Albert and Barabási 2002). In the IBOC market, a shock hitting a highly connected bank may force other banks to form a large number of new relationships and/or rely more heavily on other existing ones; either of which could cause interest rates in the IBOC market to deviate from the RBA's target and may require the RBA to supply emergency liquidity.
A network is defined as a set of ‘nodes’ (the banks) and a set of ‘links’ defining the relationships between these nodes. Links may exist between every pair of nodes, and be either ‘directed’ or ‘undirected’. Directed links contain information on the direction of the flow (e.g. a loan going from Bank A to Bank B), while undirected links only show that a flow exists (e.g. a loan between Banks A and B). Links may also be either ‘weighted’ or ‘unweighted’. Weighted links contain information on the size of the flow (e.g. a $10 million loan), while unweighted links contain no size information.
In this paper, we construct unweighted–directed networks. This is because unweighted networks are more likely to capture the relationships in which we are interested. For example, a small bank that intermediates the funding of a group of other small banks, and therefore has only small-valued links, may still be vital for ensuring an efficient distribution of liquidity. However, due to the relatively small weight of its links, a weighted network may overlook the importance of this bank.[7]
Unweighted–directed networks can be conveniently represented by an ‘adjacency matrix’. If N is the number of banks in the system, the adjacency matrix will be of dimension N × N. A link going from node i to node j (i.e. Bank i lends to Bank j) is represented by a one in the ith row and jth column of this matrix. If no link exists in this direction between these nodes, the ijth element of this matrix equals zero. Since banks do not lend to themselves in the IBOC market, the diagonal elements of our adjacency matrices will be zero. Therefore, we ignore the diagonal in all analyses in this paper.
For our baseline analysis, we aggregate our loan-level data to construct a network for each quarter in our sample, for an ensemble of 44 quarterly networks (2005:Q2–2016:Q1). We choose a quarterly frequency because even the most important IBOC relationships between banks are unlikely to be utilised on a daily basis (this is consistent with Fricke and Lux (2015)). While this frequency ensures we will capture all the important relationships (i.e. it maximises the signal from the underlying structure of the network), we will likely also capture some seldom-used links that are treated the same due to the network being unweighted (i.e. there will also be noise).
Sections 5 and 6 show that our new estimator is able to filter through this noise to obtain an accurate estimate of the time-varying core/periphery structure of the market. As a robustness check, however, we estimate the core/periphery structure at a monthly and weekly frequency. As expected, there is less signal (so the estimated core/periphery structure is more volatile), but our qualitative results remain unchanged (see Appendix E).
The remainder of this section outlines the basic network properties of the IBOC market, shows how they change over time, and demonstrates why a core/periphery model may suit the IBOC market better than other commonly used models.
3.1 Size and Density
The most basic property of a network is its ‘size’. For our networks, measures of size include the number of active banks (nodes), the number of lending/borrowing relationships (links), and the size of these relationships (i.e. the loan volumes). In each quarter, a bank is classified as ‘active’ if it has at least one link with another bank. Inactive banks are not relevant for our analysis and are therefore excluded from the network during the quarters in which they do not participate in the IBOC market.
The ‘density’ of a network, also known as the degree of completeness or connectivity, measures the proportion of links relative to the total possible number of links. It represents how well connected (directly) the nodes are in the network. For interbank markets, the higher the density, the greater the ability of banks to find alternative sources of funds when a bank withdraws from the market. Using the adjacency matrix (with the value in the ith row and jth column denoted ai,j), the density of an unweighted–directed network is calculated as:
Figure 1 shows the size and density properties of the quarterly networks in our sample. On average, 41 banks participate in the IBOC market each quarter. These banks are directly linked by, on average, around 420 directed loan relationships. The average density is 0.25, indicating that the network of IBOC loan relationships is sparse (i.e. 75 per cent of the potential links in any quarter are not used).
Although sparse, our networks have higher densities than interbank networks constructed from end-of-quarter regulatory filings. Tellez (2013), for example, maps the network of large bilateral exposures between Australian financial institutions and finds a density of less than 5 per cent. Craig and von Peter (2014) analyse an analogous network of the German banking system and find an average density of less than 1 per cent. As these networks are constructed from outstanding loans at a given point in time, and focus on large exposures only, the lower densities exhibited in these networks are not surprising.
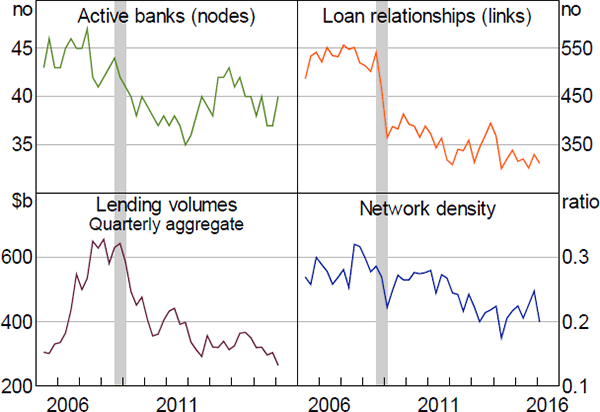
Relative to interbank networks constructed from loan-level data, our average density is higher than the 0.7 per cent computed for the US federal funds market (Bech and Atalay 2010). But it is around half the average density of the UK overnight interbank market (Wetherilt et al 2010) and is comparable to the Italian overnight interbank market (Fricke and Lux 2015).
Of particular interest in Figure 1 is the sharp decrease in the number of links at the height of the 2007–08 financial crisis (grey shaded area), with no recovery afterwards (upper-right panel); between 2008:Q3 and 2009:Q1, the number of loan relationships fell by more than 30 per cent. While only a quarter of this drop can be attributed to banks that exited the market or merged during this period, this proportion increases to 47 per cent after accounting for banks that exited/merged soon after this period (upper-left panel). It is possible that these banks curtailed their market activity before they became fully inactive; the recovery of the network density soon after the height of the crisis provides some evidence for this conjecture (lower-right panel).
Notably, the links removed between 2008:Q3 and 2009:Q1 accounted for 17 per cent of total lending/borrowing (by value) during 2008:Q3, but there was no correspondingly large change in the volumes of interbank lending during this period (lower-left panel of Figure 1). Therefore, banks must have reduced the number of their lending relationships but increased the value of lending that occurred through their remaining relationships.
Overall, this evidence suggests that the crisis has had a long-lasting impact on the structure and functioning of the IBOC market.
3.2 Degree Centrality
Another feature of networks that is relevant to our analysis is the centrality of the nodes. Centrality is a measure of the importance of each node to the network. While there are various ways to measure centrality, papers that analyse interbank market networks generally use the ‘degree centrality’ indicator. A given bank's degree centrality (henceforth, degree) is defined as the number of links that are directly attached to that bank. Its ‘in-degree’ is the number of borrowing links, while its ‘out-degree’ is the number of lending links.
Different theoretical models of networks produce different degree distributions (i.e. the distribution of degrees among the banks in the network). Comparing real-world degree distributions to theoretical ones helps researchers determine a suitable model for how a given network was formed and how the network may change with the addition/subtraction of a node/link.
3.3 Canonical Network Models
One of the most basic, but commonly used, unweighted network models is the Erdős-Rényi model. In this model, each of the N(N − 1) possible links has the same probability of existing (p), with the existence of each link being independent of the existence of any other links. With this model, the in- and out-degree distributions of the network follow the same binomial distribution; as shown in Albert and Barabási (2002), the probability of a randomly chosen node having an in-degree of k is:
Moreover, the probability of two randomly chosen nodes in this model being connected (in at least one direction) is p2 + 2p(1 − p). Therefore, the Erdős-Rényi model is not designed to produce either highly connected nodes or nodes with only a small number of links.
A commonly used model that produces both highly connected and weakly connected nodes by design is the Barabási-Albert model (see Albert and Barabási (2002) for details). In this model, networks are formed by progressively adding nodes to some small initial network (of size m0).
Denoting the addition of new nodes on a time scale (t = 1, 2,…), after each t there are Nt = t + m0 nodes (as one node is added at each point in time). Each new node forms undirected links with m ≤ m0 of the existing Nt − 1 nodes.[8] The probability of a link forming with each existing node is based on the number of links already connected to each node. If the degree of node i ∈{1,2,…,Nt −1} before time t is 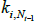 , then the unconditional probability of a link forming between the new node and node i is:
, then the unconditional probability of a link forming between the new node and node i is:
This method of adding nodes is a special case of a mechanism known as ‘preferential attachment’ – some nodes are ‘preferred’ to others. Therefore, as the network grows, the model produces a large number of weakly connected nodes and a small number of highly connected nodes.
With this model, the asymptotic degree distribution of the network follows a power law with γ = 3 (Albert and Barabási 2002):[9]
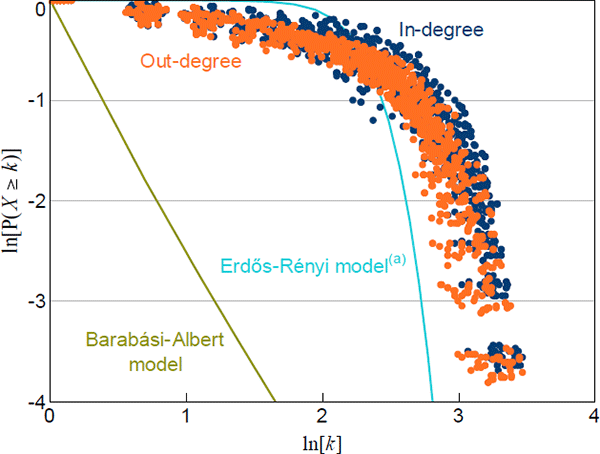
Figure 2 compares the normalised in- and out-degree distributions for every quarter in our sample to the theoretical distributions implied by the Erdős-Rényi and Barabási-Albert models. The disparity between the theoretical and data-based distributions indicates that our networks are unlikely to have been constructed from either of these theoretical models.
Notes:
For each observation, P(X ≥ k) is calculated as the share of nodes with degree ≥ k; each network is normalised to a network with the average number of nodes
(a) Calibrated to the average number of nodes and average density of the data
Additionally, the way our data deviate from these distributions is noteworthy. Not only do the degree distributions of our networks not follow the power law implied by the Barabási-Albert model (i.e. with γ = 3), they do not follow any power law (power laws would be a straight line in Figure 2). Therefore, our networks are not ‘scale-free’ (scale-free is the term used for a network whose degree distribution follows a power law).[10],[11]
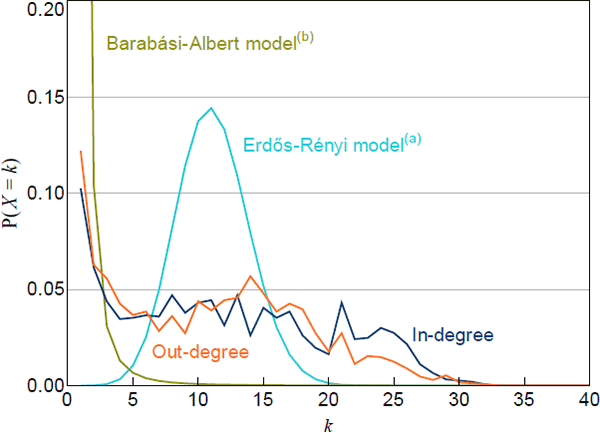
Scale-free networks produce a large number of small-degree nodes and a small number of high-degree nodes. In our networks, the most common nodes are those with small degrees, consistent with a scale-free network (Figure 3). However, high-degree nodes are more common in our networks than in a scale-free network. This is consistent with previous work on overnight interbank markets, including the US federal funds market (Bech and Atalay 2010) and the Italian market (Fricke and Lux 2015), and suggests that a ‘tiering’ model may be appropriate for our networks.
Notes:
Each network is normalised to a network with the average number of nodes
(a) Calibrated to the average number of nodes and average density of the data
(b) The value at k = 1 is 0.83
Craig and von Peter (2014, p 325) define a banking network as exhibiting tiering when:
Some banks (the top tier) lend to each other and intermediate between other banks, which participate in the interbank market only via these top-tier banks.
Because the top-tier banks lend to/borrow from each other and intermediate between the low-tier banks, top-tier banks have higher degrees than the low-tier ones.[12] Therefore, tiering models permit a larger proportion of high-degree nodes than scale-free networks.
Importantly, tiering models do not require banks within each tier to have the same degree. For example, one top-tier bank may intermediate the lending/borrowing of many low-tier banks, while another top-tier bank may only intermediate the operations of a few low-tier banks. This is a useful feature because the relatively flat probability mass functions of our networks (for mid-range degrees) suggest that banks within each tier of our networks may have varying degrees (Figure 3).
Another possibility is that our networks consist of both a tiering structure and some noise. So any method we use to identify the existence of a tiering structure must be able to distinguish between the tiering component and any noise. This is the focus of Sections 4–6 of this paper.
3.4 The Core/Periphery Model
A canonical model that exhibits tiering is the core/periphery model introduced by Borgatti and Everett (2000). When applied to interbank markets (pioneered by Craig and von Peter (2014)), the model seeks to split banks into two subsets. One subset, the ‘core’, consists of banks that are central to the system. They lend to/borrow from all other banks in the core and some banks outside of the core. Members of the other subset, the ‘periphery’, instead lend to/borrow from some core banks, but do not transact directly among themselves.
In essence, the core banks are intermediaries. But the core/periphery structure is stronger than this since funds are only able to flow between periphery banks via the core. Moreover, the core banks, through their links with each other, must be able to intermediate funding between any two banks within the system, implying that no group of banks may exist as a silo.
There are various theoretical models of financial markets that produce a core/periphery structure endogenously. In some models, some banks possess a comparative advantage in overcoming information asymmetries, searching for counterparties, or bargaining (e.g. Fricke and Lux 2015; Chiu and Monnet 2016). In other models, building relationships is costly for all banks, but large banks are more likely to require a larger number of counterparties to satisfy their desired lending/borrowing and therefore benefit from building relationships with a larger number of banks. These large banks become intermediaries because intermediaries are able to extract some of the surplus from trade; a non-trivial core size develops when competition among intermediaries is imperfect (van der Leij, in ′t Veld and Hommes 2016).
Adjacency matrices provide a convenient way to represent a core/periphery (henceforth, CP) structure. If the banks are sorted so that the lending (borrowing) of the c core banks is represented by the first c rows (columns) in the adjacency matrix, then an adjacency matrix of a CP network can be represented as four blocks:
The core block (upper-left) is a block of ones (except for the diagonal), since a CP network has all core banks lending to, and borrowing from, every other core bank. The periphery block (lower-right) is a block of zeros, since periphery banks in a CP network only lend to/borrow from core banks. The density of each block (excluding the diagonal elements of the matrix) equals the proportion of ones within that block.
The ideal CP structure of Craig and von Peter (2014) requires a core bank to lend to and borrow from at least one periphery bank (borrower and lender counterparties need not be the same). This translates into the CL (core lending) and CB (core borrowing) blocks being row- and column-regular, respectively.[13] As we discuss below, not every CP model estimator utilises the structure of these off-diagonal blocks.[14]
Real-world networks are unlikely to exactly match a theoretical CP structure. Consequently, different methods have been developed to evaluate how well a given network reflects an ideal CP structure and, assuming a core exists, estimate which banks are in the core. It is to these methods that we now turn.
Footnotes
For the same reason, much of the literature applying core/periphery models to interbank markets focuses on unweighted networks (e.g. Wetherilt et al 2010; Craig and von Peter 2014). [7]
While this model is designed to work with undirected networks, it can be applied to directed networks by using the model to construct either the in-degrees or the out-degrees (with the other degrees forming mechanically as a result of this process, but not necessarily with the same degree distribution). [8]
Where C is a constant ensuring the probabilities sum to one. [9]
Power law degree distributions are scale free because the probability of any degree is equal to the scaled probability of any other degree. That is, P(X = ak) = a−γP(X = k) where a is a positive constant. [10]
Our networks differ from many other real-world networks that appear to be scale-free (Albert and Barabási 2002), including the large-exposures networks of the Australian banking system (Tellez 2013) and the Austrian interbank market (Boss et al 2004). [11]
Quarterly networks aggregated from high-frequency data can exhibit features that are observationally equivalent to the features produced by intermediation, but are actually caused by the aggregation process. In Appendix F we use the high-frequency data to provide evidence that the tiering structure exhibited in our quarterly networks actually reflects intermediation. [12]
Row (column) regularity means that each row (column) in the block must contain at least one non-zero element. [13]
The CP model can be adjusted to consider each node as having some amount of ‘coreness’. This is done for weighted networks in Borgatti and Everett (2000) and Fricke and Lux (2015), and for both weighted and unweighted networks in the random-walker model of Della Rossa, Dercole and Piccardi (2013), for example. We do not consider these alternatives because these models do not allow any structure to be placed on the off-diagonal blocks, and would require the imposition of an arbitrary coreness cut-off to determine which banks are in the core and how the size of the core has changed over time. [14]