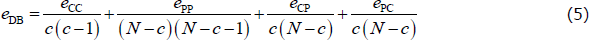RDP 2018-01: A Density-based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market 5. The Density-based Estimator

The inaccuracy of the CvP estimator results from a focus on the number of errors rather than the density of errors. In Section 4.4, incorrectly classifying banks increases the density of errors in one of the diagonal blocks (i.e. the core or periphery block) and leaves the density of errors in the other diagonal block unchanged. But with some parameterisations this move reduces the total number of errors, so the move is optimal for the CvP estimator.

To overcome this problem, we construct a new estimator that focuses on the density of errors within each block (henceforth, the density-based, or DB, estimator). We do this by dividing each error block in the CvP error function (Equation (3)) by the number of possible errors within that block.^[20] Therefore, the DB estimator is the CP split that minimises the following error function:

With the simplifying assumptions from Section 4.4, the global optimum of the density-based estimator is c = c_T (see Appendix B for the proof).

The intuition behind this result is as follows. Setting y > 0 causes the density of the core block to fall, and either has no effect on the density of the periphery block (if x = 0) or causes it to increase (if x > 0).^[21] Therefore, y > 0 cannot be optimal. Similarly, setting x > 0 causes the density of the periphery block to increase, while either reducing the density of the core block (if y > 0) or leaving it unchanged (if y = 0). Therefore, x > 0 cannot be optimal.

This result does not depend on the values of the network parameters {d_C, d_O, d_P, c_T}. Therefore, with the simplifying assumptions, increasing the expected number of errors (i.e. increasing d_P or decreasing d_C) has no effect on the DB estimator. To determine the accuracy of the DB estimator when the simplifying assumptions are removed, we turn to numerical simulations.

Footnotes

Cucuringu et al (2016) recently derived a similar estimator independently of Craig and von Peter (2014). There are, however, some important differences between our DB estimator and the estimator proposed by Cucuringu et al, with the theoretical performance of their two-step estimator being no better than our one-step estimator. This is discussed in Appendix C. [20]

Recall that x is the share of banks that are true-core banks but are placed in the periphery, and y is the share of banks that are true-periphery banks but are placed in the core. [21]