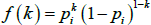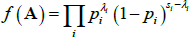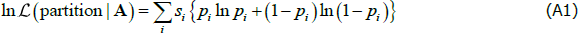RDP 2018-01: A Density-based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market Appendix A: The Maximum Likelihood Estimator
February 2018
- Download the Paper 1,628KB
Partition the N × N adjacency matrix (A) into four blocks: the core lends to core block, the core lends to periphery block, the periphery lends to core block, and the periphery lends to periphery block. Assuming the links in each block come from an Erdős-Rényi random network, the probability mass function for a link in block i is a Bernoulli distribution (with support k ∈ {0,1} and probability pi):
Since each link in an Erdős-Rényi network is independent, the joint probability function of all the links in the adjacency matrix is the product of N(N − 1) Bernoulli distributions:
where si is the number of possible links in block i and λi is the number of actual links in block i. With each bank's designation as core or periphery determining the composition of the four blocks, the joint probability distribution is defined by N + 4 parameters (the designations of the N banks, and the four pi parameters).
Both si and λi depend on the matrix A and on the core/periphery partition, but not on the probability pi. Therefore, we can determine the maximum likelihood estimator of pi conditional on the data and the core/periphery partition in order to produce a concentrated log-likelihood function where the only unknown parameters are whether each node is in the core or the periphery.
The conditional maximum likelihood estimator of pi is λi/si. However, for our analysis it is handy to concentrate-out the λi parameter so that the concentrated log-likelihood function becomes:
where pi is now a function of the data and the core/periphery partition via the relationship λi = sipi.
For a given core/periphery partition, the log-likelihood has the same value if the designation of every bank is switched (i.e. every core bank becomes a periphery bank and every periphery bank becomes a core bank). Therefore, the maximum likelihood estimator requires the identifying restriction pCC ≥ pPP (where i = CC is the block of core lends to core links and i = PP is the block of periphery lends to periphery links).
Since pi ∈[0,1], each component of the sum in Equation (A1) is bounded above by zero.[32] This upper bound occurs when either pi = 0 or pi = 1. Since pi = λi/si, the upper bound for each component is reached when either no links exist in the corresponding block or all the links in the block exist. Therefore, if we ignore the components of Equation (A1) that correspond to the off-diagonal blocks, the true CP split of an ideal CP network produces the largest possible value of the likelihood function.
Footnote
Evaluating xlnx when x = 0 as its limit value as x → 0 (to prevent the log-likelihood from being undefined at the bounds of pi). [32]