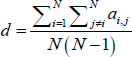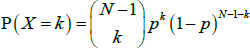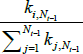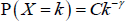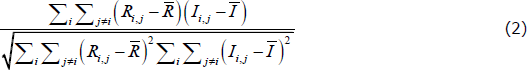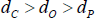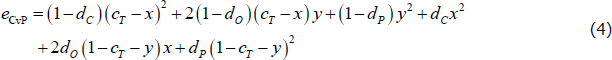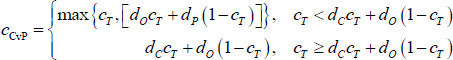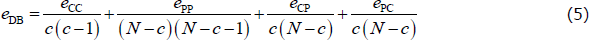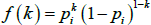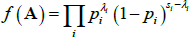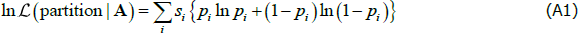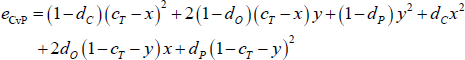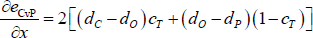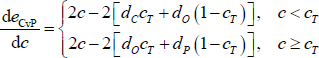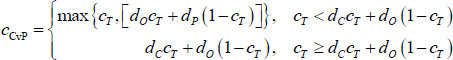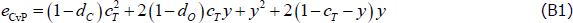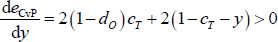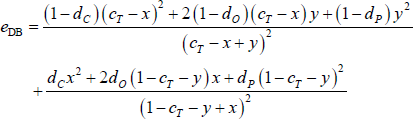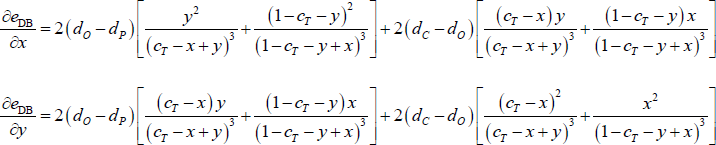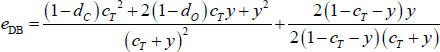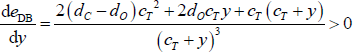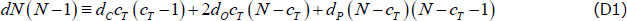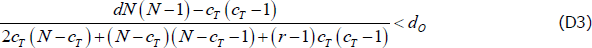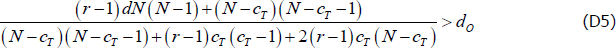Research Discussion Paper – RDP 2018-01 A Density-based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market
1. Introduction
Seizures in the electricity grid, degradation of eco-systems, the spread of epidemics and the disintegration of the financial system – each is essentially a different branch of the same network family tree. Haldane (2009)
The market for unsecured overnight interbank loans in Australia, known as the interbank overnight cash (IBOC) market, is a pivotal financial market. The average interest rate on these loans is the Reserve Bank of Australia's (RBA) operational target for monetary policy; so the IBOC market is the first step in the transmission of monetary policy to the rest of the financial system and broader economy. As such, its smooth operation is critical, and it is important for the RBA to have detailed knowledge about how it functions, especially in times of stress.
In this paper, we explore the IBOC market through the lens of network theory.[1] Network theory allows us to identify the lending relationships formed by banks, determine whether these relationships make any of the banks central to the proper functioning of the market, and analyse how these relationships may change during periods of stress. The answers to these questions provide a guide to which interbank relationships are resilient, whether crises can have long-lasting effects on the IBOC market, and how to efficiently manage emergency liquidity provision (e.g. liquidity provision could be more targeted if we know the relationships between the banks).
This paper also has a theoretical contribution. First, we find that several of the IBOC market's network properties are consistent with the core/periphery model (first introduced by Borgatti and Everett (2000) and adjusted to capture the features specific to interbank markets by Craig and von Peter (2014)). The premise of the core/periphery model is that there are two types of banks. ‘Core’ banks are central to the system; they lend to/borrow from all other banks in the core and to some banks outside of the core. ‘Periphery’ banks, instead, lend to/borrow from some core banks, but do not transact directly among themselves. Thus, the removal of a core bank can inhibit the flow of funds and drastically change the structure of the network.
There have recently been several studies that analyse interbank markets with the core/periphery model.[2] And with real-world networks being unlikely to satisfy the idealiseds core/periphery structure outlined above, various methods have been developed to estimate the underlying core/periphery structure of these networks.[3] However, as far as we are aware, no-one has evaluated the various estimators' relative accuracies. This paper fills this gap.
We find that existing estimators can provide wildly varying and inaccurate estimates in networks that have either a relatively large or relatively small core (relative to the density of the network, a concept explained in Section 3). We analytically derive the source of this problem, and then derive a new estimator that is immune to this source of inaccuracy. In numerical simulations, our estimator produces lower estimation errors than any of the commonly used estimators when either the true size of the core is known to be relatively small, or when no prior information about the true size of the core is available.
Our new estimator can be used on any network that may have a core/periphery structure. Therefore, given the increasing use of the core/periphery model when analysing networks, our theoretical contribution has broad applicability.
Returning to our empirical contribution, we show that the core/periphery model provides a better explanation of the IBOC market's features than other canonical network models. So we use this model (with our estimator) to analyse the evolution of the market during the 2007–08 financial crisis. Prior to the crisis, the IBOC market had a core of around eight banks – the core typically included the four major Australian banks, three foreign-owned banks, and one other Australian-owned bank. The financial crisis caused the core to shrink to around five banks – the four major banks and one foreign-owned bank – with the core remaining around this size in the years since the crisis. This finding suggests that not all relationships are reliable during times of stress. It also indicates that temporary shocks can have long-lasting effects on the IBOC market, which is important not only for determining the effect of exogenous shocks but also for evaluating the potential effect of any operational changes made by the RBA.
We also look at changes in the relationships between the core and periphery. We find that the number of ‘core lending to periphery’ relationships fell 40 per cent during 2008 (the largest year-on-year fall in our sample) and continued to trend down following the crisis. Conversely, the number of ‘periphery lending to core’ relationships remained broadly unchanged.
Additionally, we uncover a large shift in the direction of lending volumes. The major banks were net lenders to the non-major banks before the crisis. During the crisis, this relationship switched – in 2008 the volume of major banks' loans to non-major banks decreased by 58 per cent, while the volume of loans in the reverse direction increased by 84 per cent. The non-major banks have remained net lenders to the major banks since the crisis, albeit at a lower level than during 2008–09.
Irrespective of whether it was the core actively reducing their exposure to the periphery, or the periphery reducing their reliance on the core (due to fears about the reliability of their funding), these trends are consistent with the predictions of theoretical models of precautionary liquidity demand during periods of heightened risk (Ashcraft, McAndrews and Skeie 2011).
2. The Interbank Overnight Cash Market
Banks use the market for unsecured overnight interbank loans (IBOC market) to manage their liquidity.[4] Specifically, banks' deposit accounts with the RBA, which are used to settle the financial obligations arising from interbank payments, must remain in credit at all times. Banks borrow in the IBOC market to ensure they satisfy this requirement (as the cost of overnight borrowing from the RBA is higher than the typical IBOC market rate). The RBA also remunerates surplus balances in banks' deposit accounts at a rate below the typical IBOC market rate; banks, therefore, have an incentive to lend their surplus balances in the IBOC market.
The IBOC market also plays a role in disseminating private information. Loans in the IBOC market are transacted bilaterally and over-the-counter. Failure to raise sufficient liquidity through banks' usual relationships – due to liquidity hoarding, for example – could lead to increased counterparty searching, potentially signalling to the RBA and other banks an increase in idiosyncratic or market risk.
The RBA, and many other central banks, have historically relied on surveys to collect information about overnight interbank markets. But these survey data are typically highly aggregated. For example, until May 2016, the RBA's IBOC Survey only provided the aggregate gross value of each survey participant's IBOC lending and borrowing during each trading session of the day, and the average interest rate at which these loans occurred (importantly, no information on counterparties was collected).[5]
To overcome this deficiency, Brassil, Hughson and McManus (2016) developed an algorithm to extract loan-level information from Australia's real-time gross settlement system (all IBOC loans, and many other interbank payments, are settled through this system). This algorithm is based on the seminal work of Furfine (1999), but incorporates novel features to identify IBOC loans that are rolled over multiple days, including those that exhibit features similar to a credit facility (e.g. drawdowns and partial repayments).
The algorithm output provides us with a loan-level database of IBOC loans between 2005 and 2016 (the algorithm identifies close to 90 per cent of all loans during this period, see Brassil et al (2016)). This database consists of 62 banks and 147,380 IBOC loans. Banks are split into three categories: the four major Australian banks, other Australian-owned banks, and foreign-owned banks.[6] We use this database to construct the networks analysed in this paper.
Using a loan-level database to conduct a network analysis has several advantages. Unlike networks constructed from regulatory databases of banks' large exposures, a loan-level database allows us to consider the role played by small banks. This is particularly relevant when estimating core/periphery structures, as the omission of exposures to smaller banks could prevent some highly connected banks from being identified as such. A loan-level database also allows us to conduct our network analysis using all loans during a particular period (not just those at the end of each quarter), and at different frequencies (quarterly, monthly, weekly, etc). That said, loan-level databases do not typically cover as wide an array of markets as regulatory databases.
3. The Network Structure of the IBOC Market
Studying the IBOC market as a ‘network’ allows us to better understand how the banks are related and the importance of each bank to the proper functioning of the market. It is well known that certain network structures are more prone to disruption than others. For example, shocks are more likely to propagate through highly connected networks, but the effect on each part of the network may be small (Allen and Gale 2000). Conversely, in weakly connected networks, the effect of most shocks will be localised, but a small number of highly connected banks could make the system fragile to shocks hitting one of these banks (Albert and Barabási 2002). In the IBOC market, a shock hitting a highly connected bank may force other banks to form a large number of new relationships and/or rely more heavily on other existing ones; either of which could cause interest rates in the IBOC market to deviate from the RBA's target and may require the RBA to supply emergency liquidity.
A network is defined as a set of ‘nodes’ (the banks) and a set of ‘links’ defining the relationships between these nodes. Links may exist between every pair of nodes, and be either ‘directed’ or ‘undirected’. Directed links contain information on the direction of the flow (e.g. a loan going from Bank A to Bank B), while undirected links only show that a flow exists (e.g. a loan between Banks A and B). Links may also be either ‘weighted’ or ‘unweighted’. Weighted links contain information on the size of the flow (e.g. a $10 million loan), while unweighted links contain no size information.
In this paper, we construct unweighted–directed networks. This is because unweighted networks are more likely to capture the relationships in which we are interested. For example, a small bank that intermediates the funding of a group of other small banks, and therefore has only small-valued links, may still be vital for ensuring an efficient distribution of liquidity. However, due to the relatively small weight of its links, a weighted network may overlook the importance of this bank.[7]
Unweighted–directed networks can be conveniently represented by an ‘adjacency matrix’. If N is the number of banks in the system, the adjacency matrix will be of dimension N × N. A link going from node i to node j (i.e. Bank i lends to Bank j) is represented by a one in the ith row and jth column of this matrix. If no link exists in this direction between these nodes, the ijth element of this matrix equals zero. Since banks do not lend to themselves in the IBOC market, the diagonal elements of our adjacency matrices will be zero. Therefore, we ignore the diagonal in all analyses in this paper.
For our baseline analysis, we aggregate our loan-level data to construct a network for each quarter in our sample, for an ensemble of 44 quarterly networks (2005:Q2–2016:Q1). We choose a quarterly frequency because even the most important IBOC relationships between banks are unlikely to be utilised on a daily basis (this is consistent with Fricke and Lux (2015)). While this frequency ensures we will capture all the important relationships (i.e. it maximises the signal from the underlying structure of the network), we will likely also capture some seldom-used links that are treated the same due to the network being unweighted (i.e. there will also be noise).
Sections 5 and 6 show that our new estimator is able to filter through this noise to obtain an accurate estimate of the time-varying core/periphery structure of the market. As a robustness check, however, we estimate the core/periphery structure at a monthly and weekly frequency. As expected, there is less signal (so the estimated core/periphery structure is more volatile), but our qualitative results remain unchanged (see Appendix E).
The remainder of this section outlines the basic network properties of the IBOC market, shows how they change over time, and demonstrates why a core/periphery model may suit the IBOC market better than other commonly used models.
3.1 Size and Density
The most basic property of a network is its ‘size’. For our networks, measures of size include the number of active banks (nodes), the number of lending/borrowing relationships (links), and the size of these relationships (i.e. the loan volumes). In each quarter, a bank is classified as ‘active’ if it has at least one link with another bank. Inactive banks are not relevant for our analysis and are therefore excluded from the network during the quarters in which they do not participate in the IBOC market.
The ‘density’ of a network, also known as the degree of completeness or connectivity, measures the proportion of links relative to the total possible number of links. It represents how well connected (directly) the nodes are in the network. For interbank markets, the higher the density, the greater the ability of banks to find alternative sources of funds when a bank withdraws from the market. Using the adjacency matrix (with the value in the ith row and jth column denoted ai,j), the density of an unweighted–directed network is calculated as:
Figure 1 shows the size and density properties of the quarterly networks in our sample. On average, 41 banks participate in the IBOC market each quarter. These banks are directly linked by, on average, around 420 directed loan relationships. The average density is 0.25, indicating that the network of IBOC loan relationships is sparse (i.e. 75 per cent of the potential links in any quarter are not used).
Although sparse, our networks have higher densities than interbank networks constructed from end-of-quarter regulatory filings. Tellez (2013), for example, maps the network of large bilateral exposures between Australian financial institutions and finds a density of less than 5 per cent. Craig and von Peter (2014) analyse an analogous network of the German banking system and find an average density of less than 1 per cent. As these networks are constructed from outstanding loans at a given point in time, and focus on large exposures only, the lower densities exhibited in these networks are not surprising.
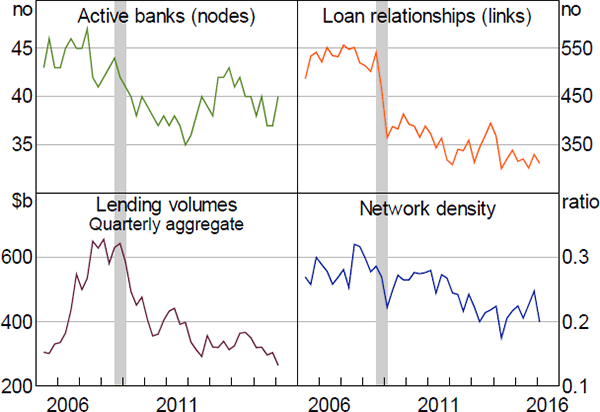
Relative to interbank networks constructed from loan-level data, our average density is higher than the 0.7 per cent computed for the US federal funds market (Bech and Atalay 2010). But it is around half the average density of the UK overnight interbank market (Wetherilt et al 2010) and is comparable to the Italian overnight interbank market (Fricke and Lux 2015).
Of particular interest in Figure 1 is the sharp decrease in the number of links at the height of the 2007–08 financial crisis (grey shaded area), with no recovery afterwards (upper-right panel); between 2008:Q3 and 2009:Q1, the number of loan relationships fell by more than 30 per cent. While only a quarter of this drop can be attributed to banks that exited the market or merged during this period, this proportion increases to 47 per cent after accounting for banks that exited/merged soon after this period (upper-left panel). It is possible that these banks curtailed their market activity before they became fully inactive; the recovery of the network density soon after the height of the crisis provides some evidence for this conjecture (lower-right panel).
Notably, the links removed between 2008:Q3 and 2009:Q1 accounted for 17 per cent of total lending/borrowing (by value) during 2008:Q3, but there was no correspondingly large change in the volumes of interbank lending during this period (lower-left panel of Figure 1). Therefore, banks must have reduced the number of their lending relationships but increased the value of lending that occurred through their remaining relationships.
Overall, this evidence suggests that the crisis has had a long-lasting impact on the structure and functioning of the IBOC market.
3.2 Degree Centrality
Another feature of networks that is relevant to our analysis is the centrality of the nodes. Centrality is a measure of the importance of each node to the network. While there are various ways to measure centrality, papers that analyse interbank market networks generally use the ‘degree centrality’ indicator. A given bank's degree centrality (henceforth, degree) is defined as the number of links that are directly attached to that bank. Its ‘in-degree’ is the number of borrowing links, while its ‘out-degree’ is the number of lending links.
Different theoretical models of networks produce different degree distributions (i.e. the distribution of degrees among the banks in the network). Comparing real-world degree distributions to theoretical ones helps researchers determine a suitable model for how a given network was formed and how the network may change with the addition/subtraction of a node/link.
3.3 Canonical Network Models
One of the most basic, but commonly used, unweighted network models is the Erdős-Rényi model. In this model, each of the N(N − 1) possible links has the same probability of existing (p), with the existence of each link being independent of the existence of any other links. With this model, the in- and out-degree distributions of the network follow the same binomial distribution; as shown in Albert and Barabási (2002), the probability of a randomly chosen node having an in-degree of k is:
Moreover, the probability of two randomly chosen nodes in this model being connected (in at least one direction) is p2 + 2p(1 − p). Therefore, the Erdős-Rényi model is not designed to produce either highly connected nodes or nodes with only a small number of links.
A commonly used model that produces both highly connected and weakly connected nodes by design is the Barabási-Albert model (see Albert and Barabási (2002) for details). In this model, networks are formed by progressively adding nodes to some small initial network (of size m0).
Denoting the addition of new nodes on a time scale (t = 1, 2,…), after each t there are Nt = t + m0 nodes (as one node is added at each point in time). Each new node forms undirected links with m ≤ m0 of the existing Nt − 1 nodes.[8] The probability of a link forming with each existing node is based on the number of links already connected to each node. If the degree of node i ∈{1,2,…,Nt −1} before time t is 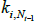 , then the unconditional probability of a link forming between the new node and node i is:
, then the unconditional probability of a link forming between the new node and node i is:
This method of adding nodes is a special case of a mechanism known as ‘preferential attachment’ – some nodes are ‘preferred’ to others. Therefore, as the network grows, the model produces a large number of weakly connected nodes and a small number of highly connected nodes.
With this model, the asymptotic degree distribution of the network follows a power law with γ = 3 (Albert and Barabási 2002):[9]
Figure 2 compares the normalised in- and out-degree distributions for every quarter in our sample to the theoretical distributions implied by the Erdős-Rényi and Barabási-Albert models. The disparity between the theoretical and data-based distributions indicates that our networks are unlikely to have been constructed from either of these theoretical models.
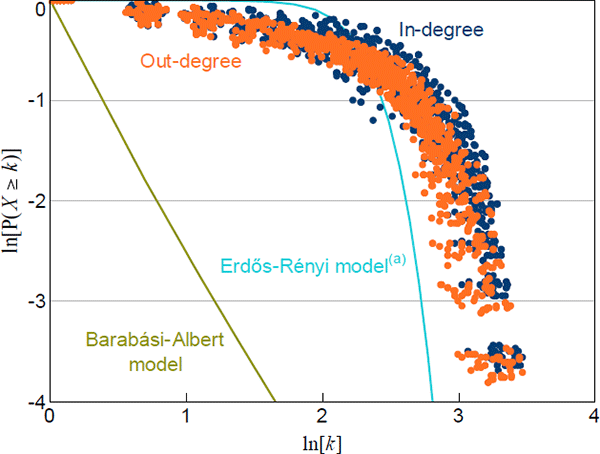
Notes:
For each observation, P(X ≥ k) is calculated as the share of nodes with degree ≥ k; each network is normalised to a network with the average number of nodes
(a) Calibrated to the average number of nodes and average density of the data
Additionally, the way our data deviate from these distributions is noteworthy. Not only do the degree distributions of our networks not follow the power law implied by the Barabási-Albert model (i.e. with γ = 3), they do not follow any power law (power laws would be a straight line in Figure 2). Therefore, our networks are not ‘scale-free’ (scale-free is the term used for a network whose degree distribution follows a power law).[10],[11]
Scale-free networks produce a large number of small-degree nodes and a small number of high-degree nodes. In our networks, the most common nodes are those with small degrees, consistent with a scale-free network (Figure 3). However, high-degree nodes are more common in our networks than in a scale-free network. This is consistent with previous work on overnight interbank markets, including the US federal funds market (Bech and Atalay 2010) and the Italian market (Fricke and Lux 2015), and suggests that a ‘tiering’ model may be appropriate for our networks.
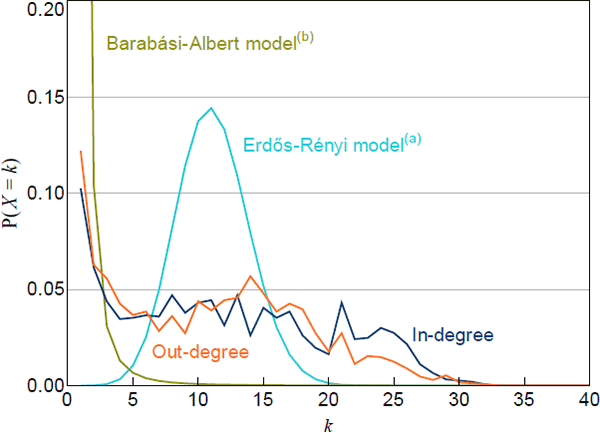
Notes:
Each network is normalised to a network with the average number of nodes
(a) Calibrated to the average number of nodes and average density of the data
(b) The value at k = 1 is 0.83
Craig and von Peter (2014, p 325) define a banking network as exhibiting tiering when:
Some banks (the top tier) lend to each other and intermediate between other banks, which participate in the interbank market only via these top-tier banks.
Because the top-tier banks lend to/borrow from each other and intermediate between the low-tier banks, top-tier banks have higher degrees than the low-tier ones.[12] Therefore, tiering models permit a larger proportion of high-degree nodes than scale-free networks.
Importantly, tiering models do not require banks within each tier to have the same degree. For example, one top-tier bank may intermediate the lending/borrowing of many low-tier banks, while another top-tier bank may only intermediate the operations of a few low-tier banks. This is a useful feature because the relatively flat probability mass functions of our networks (for mid-range degrees) suggest that banks within each tier of our networks may have varying degrees (Figure 3).
Another possibility is that our networks consist of both a tiering structure and some noise. So any method we use to identify the existence of a tiering structure must be able to distinguish between the tiering component and any noise. This is the focus of Sections 4–6 of this paper.
3.4 The Core/Periphery Model
A canonical model that exhibits tiering is the core/periphery model introduced by Borgatti and Everett (2000). When applied to interbank markets (pioneered by Craig and von Peter (2014)), the model seeks to split banks into two subsets. One subset, the ‘core’, consists of banks that are central to the system. They lend to/borrow from all other banks in the core and some banks outside of the core. Members of the other subset, the ‘periphery’, instead lend to/borrow from some core banks, but do not transact directly among themselves.
In essence, the core banks are intermediaries. But the core/periphery structure is stronger than this since funds are only able to flow between periphery banks via the core. Moreover, the core banks, through their links with each other, must be able to intermediate funding between any two banks within the system, implying that no group of banks may exist as a silo.
There are various theoretical models of financial markets that produce a core/periphery structure endogenously. In some models, some banks possess a comparative advantage in overcoming information asymmetries, searching for counterparties, or bargaining (e.g. Fricke and Lux 2015; Chiu and Monnet 2016). In other models, building relationships is costly for all banks, but large banks are more likely to require a larger number of counterparties to satisfy their desired lending/borrowing and therefore benefit from building relationships with a larger number of banks. These large banks become intermediaries because intermediaries are able to extract some of the surplus from trade; a non-trivial core size develops when competition among intermediaries is imperfect (van der Leij, in ′t Veld and Hommes 2016).
Adjacency matrices provide a convenient way to represent a core/periphery (henceforth, CP) structure. If the banks are sorted so that the lending (borrowing) of the c core banks is represented by the first c rows (columns) in the adjacency matrix, then an adjacency matrix of a CP network can be represented as four blocks:
The core block (upper-left) is a block of ones (except for the diagonal), since a CP network has all core banks lending to, and borrowing from, every other core bank. The periphery block (lower-right) is a block of zeros, since periphery banks in a CP network only lend to/borrow from core banks. The density of each block (excluding the diagonal elements of the matrix) equals the proportion of ones within that block.
The ideal CP structure of Craig and von Peter (2014) requires a core bank to lend to and borrow from at least one periphery bank (borrower and lender counterparties need not be the same). This translates into the CL (core lending) and CB (core borrowing) blocks being row- and column-regular, respectively.[13] As we discuss below, not every CP model estimator utilises the structure of these off-diagonal blocks.[14]
Real-world networks are unlikely to exactly match a theoretical CP structure. Consequently, different methods have been developed to evaluate how well a given network reflects an ideal CP structure and, assuming a core exists, estimate which banks are in the core. It is to these methods that we now turn.
4. Existing Core/Periphery Estimators
For any given assignment of banks into core and periphery subsets (henceforth, CP split), the differences between the real-world network and the idealised CP structure create ‘errors’. For example, a link between two periphery banks is an error, as is a missing link between two core banks. Therefore, changing the CP split (e.g. changing a bank's designation from core to periphery) may change the total number of errors.
All estimation methods presented in this section are (either explicitly or implicitly) based on minimising these errors. If the real-world network coincided exactly with the ideal CP structure, the differences between these estimators would not matter (i.e. they would all identify the ideal CP structure as being the CP structure of the network). But since such a scenario is unlikely, each method can lead to a different conclusion.
After describing the key methods available in the literature, we show how their relative performance may depend on the features of the network, such as the density.[15] In Section 4.4, we analytically show how one of the commonly used estimators can be an inaccurate estimator of the size of the core. We then derive a density-based estimator that is immune to the source of this inaccuracy (Section 5). Section 6 numerically evaluates the relative performance of the various estimators (including our new estimator) when applied to simulated networks with the same features as our data. Our estimator is the best-performing estimator when applied to these simulated networks.
4.1 The Correlation Estimator
For any given CP split of a network we can produce both an ideal CP adjacency matrix (Equation (1)) and an adjacency matrix where each of the nodes is in the same position as in the ideal matrix, but the links are based on the links in the data.
Looking only at the core (upper-left) and periphery (lower-right) blocks of the two adjacency matrices, suppose we computed the Pearson correlation coefficient (henceforth, correlation) between the elements of the ideal adjacency matrix and the elements of the real-world matrix. One way to estimate the CP structure of the network is to find the CP split that maximises this correlation.[16] This is the method used by Borgatti and Everett (2000) and Boyd, Fitzgerald and Beck (2006), for example. Specifically, the correlation estimator finds the CP split that maximises the following function:
where the sums only occur over elements in the core and periphery blocks, Ri,j is the ijth element in the real-world adjacency matrix, 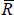 is the average of these elements, and Ii,j and
is the average of these elements, and Ii,j and 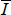 are the equivalent variables from the ideal set.
are the equivalent variables from the ideal set.
Each element of the sum in the numerator will be positive if Ri,j = Ii,j (i.e. if there is no error), and will be negative otherwise. It is in this sense that the correlation estimator is an error-minimisation method. With this property, it is tempting to think that the correlation-maximising CP split is also the split that minimises the number of errors. However, any change in the CP split will change the values of 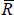 ,
,  , and the denominator. So the CP split that maximises Equation (2) may not minimise the number of errors.
, and the denominator. So the CP split that maximises Equation (2) may not minimise the number of errors.
If the real-world network exhibits an ideal CP structure, then there exists a CP split where the correlation function equals one (the maximum possible value). Therefore, if the real-world network has an ideal CP structure, this structure will be identified by this estimator.
4.2 The Maximum Likelihood Estimator
Wetherilt et al (2010) use a maximum likelihood approach similar to Copic, Jackson and Kirman (2009) to estimate the set of core banks in the UK unsecured overnight interbank market.[17]
Unlike the other estimators outlined in this section, this method makes a parametric assumption about the probability distribution of links within the network; the parametric assumption is a special case of the stochastic block model (Zhang et al 2015). Specifically, for a given CP split, this method assumes that the links in each of the blocks of the real-world adjacency matrix have been generated from an Erdős-Rényi random network, with the parameter that defines the Erdős-Rényi network allowed to differ between blocks. This leads to a likelihood function that is the product of N(N − 1) Bernoulli distributions, as shown in Appendix A.
In Appendix A, we also show that the likelihood of each block is maximised if the elements of the block are either all ones or all zeros. So, if we ignore the off-diagonal blocks, the true CP split of an ideal CP network produces the largest possible value of the likelihood function.[18] Therefore, the likelihood estimator will find the true CP structure if it satisfies the features of an ideal CP structure.
However, while correctly specified maximum likelihood estimators are known to have good asymptotic properties, it is not clear how this estimator will perform against other estimators with real-world networks (especially with N + 4 parameters to estimate, see Appendix A). Even with large unweighted networks, Copic et al (2009, p16) state that ‘there will often be a nontrivial probability that the estimated community structure will not be the true one’. Smaller networks, and CP structures that do not satisfy the estimator's parametric assumption, will likely make this problem worse.
4.3 The Craig and von Peter (2014) Estimator
The Craig and von Peter (2014) estimator (henceforth, CvP estimator) is an explicit error-minimisation method that has been used in multiple subsequent studies (e.g. in ′t Veld and van Lelyveld 2014; Fricke and Lux 2015). This estimator chooses the CP split that minimises the number of errors from comparing the corresponding ideal adjacency matrix to the real-world adjacency matrix:[19]
where, for a given CP split, eCC is the number of errors within the core block (caused by missing links) and ePP is the number of errors within the periphery block (caused by the existence of links).
As noted earlier, an ideal CP structure requires each core bank to lend to and borrow from at least one periphery bank. In the CvP estimator, if a core bank fails the lending requirement, this causes an error equal to N − c (i.e. the number of periphery banks to which the core bank could have lent); borrowing errors are computed in an analogous way. These lending and borrowing errors are captured in eCP and ePC, respectively.
4.4 Theoretical Analysis of the Craig and von Peter (2014) Estimator
An accurate estimator of the true CP structure should not be influenced by the addition of noise. In other words, the existence of some random links between periphery banks, or the absence of some random links within the core, should not systematically bias an accurate estimator. In this section, we evaluate how the addition of noise influences the CvP estimator.
A feature of the CvP estimator is that a link between two periphery banks has the same effect on the error function (Equation (3)) as a missing link between two core banks. At face value, this is reasonable; the ‘distance’ from the idealised CP structure is the same in both cases. But this equal weighting does not account for the expected number of errors within each block, and has important implications for the performance of the CvP estimator.
For example, take a true-core block of size 4 and a true-periphery block of size 36, and start with the correct partition. Moving a true-periphery bank into the core causes a maximum of eight additional errors within the core block (i.e. potential missing lending and borrowing links with the four other core banks). Even if this moved bank had no links with the true-core banks, if it had more than eight links with other true-periphery banks due to idiosyncratic noise (out of 2 × 35 possible links), and these links included at least one lending and at least one borrowing link, moving it into the core would reduce the total number of errors. Therefore, the CvP estimator would overestimate the size of the core in this scenario.
While this is just a stylised example, something like this is actually a high probability event; with even a small amount of noise (e.g. a periphery-block error density of just 0.06), the probability of there being a true-periphery bank with more than eight within-periphery links is over 50 per cent. So, with this CP structure, there is a high probability that the CvP estimator would overestimate the size of the core.
The problem is, that with this CP structure (i.e. when the periphery block is much larger than the core block) even a small amount of noise is expected to produce a sufficiently large number of periphery-block errors that an overestimate becomes the optimal response of the CvP estimator. If, on the other hand, an estimator depended not on the number of errors within each block but the proportion of block elements that are errors, it would implicitly account for the fact that larger blocks can produce a larger number of errors, and would therefore not be subject to the same problem. It is this idea that guides the derivation of our ‘density-based’ estimator in Section 5.
But before deriving our estimator, we must evaluate this problem more generally. To simplify the analysis, we focus only on the performance of the CvP estimator in determining the true size of the core (as opposed to determining which banks are in the core). We focus on the CvP estimator because the simple form of this estimator's error function allows us to analytically evaluate the sources of inaccuracy.
4.4.1 Simplifying assumptions
Our analysis uses three simplifying assumptions:
Assumption 1: Continuum of banks
We assume the network consists of a continuum of banks normalised to the unit interval [0,1]; so each individual bank has an infinitesimal effect on the CvP error function. Therefore, N = 1, and c can be interpreted as the share of banks in the core.
Assumption 2: Banks are representative
We are able to focus on core-size estimation by assuming that any subset of true-periphery banks has the same effect on the CvP error function as any other equal-sized subset of true-periphery banks. In other words, with respect to the error function, each equal-sized subset of true-periphery banks is identical.
We make the same assumption for the true-core banks (i.e. with respect to the error function, each equal-sized subset of true-core banks is identical). Another way to think about Assumptions 1 and 2 is that we have a continuum of representative true-core banks and a continuum of representative true-periphery banks.
Assumption 3: The core/periphery model is appropriate
If a network consists of a true core/periphery structure and ‘noise’, we do not expect the noise to be the dominant feature of the network; if it were to dominate, it would be more appropriate to model what is causing the noise rather than using a core/periphery model. So we assume that the noise does not cause too large a deviation of the network from a true core/periphery structure. Specifically, we assume:
where dC is the density of links within the true-core block, dO is the density of links within the true off-diagonal blocks, and dP is the density of links within the true-periphery block.
With this set-up, noise is added to the ideal CP structure by removing links from the core (i.e. setting dC < 1) and/or adding links to the periphery (i.e. setting dP > 0).
4.4.2 Impact of the simplifying assumptions
Without these simplifying assumptions, the sorted adjacency matrix of a hypothetical network with a core/periphery structure and some noise would look something like the left panel of Figure 4. As detailed in Section 3.4, each row/column in this matrix represents a bank's lending/borrowing. Banks are sorted so that the banks placed in the core are first; the red lines partition the matrix into the core, periphery, and off-diagonal blocks described in Equation (1). Black cells represent the existence of a link, white cells indicate non-existence.
With our simplifying assumptions, a hypothetical sorted adjacency matrix (with the true CP split identified) would look more like the right panel of Figure 4. This is because:
- Having a continuum of banks (Assumption 1) means each individual bank has measure zero. As a result, individual elements of the adjacency matrix have measure zero; hence the right panel is shaded instead of having individual elements like the left panel. This also means the diagonal elements of the adjacency matrix (i.e. the elements excluded because banks do not lend to themselves) have measure zero. This implies, for example, that there are c2 potential errors in a core block of size c, rather than the c(c − 1) in the integer version.
- Having representative banks (Assumption 2) means the density of links within any subset of true-periphery banks is the same as for any other subset of true-periphery banks; this is also true for the density of links between this subset and the true core. If this were not the case, some subsets would have a different effect on the CvP error function, violating Assumption 2. Analogous reasoning applies to the true-core banks. As a result, the entirety of each true CP block has the same shade.

Notes:
The red lines partition the matrix as described in Equation (1)
(a) Black cells indicate a one in the adjacency matrix, white cells indicate a zero
(b) Darker shading indicates a higher density of links within the block (black represents a density of one, white represents a density of zero)
Without the simplifying assumptions, the CP split is defined by N binary variables (each bank must be defined as either core or periphery). The advantage of having the adjacency matrix look like the right panel of Figure 4 is that the CP split becomes defined by just two variables, the share of banks that are in the true core but are placed in the periphery (x) and the share of banks that are in the true periphery but are placed in the core (y). Denoting the true share of banks that are in the core as cT, then x∈[0,cT], y∈[0,1 − cT], and the share of banks placed in the core (i.e. the CP split) is c = cT − x + y. An accurate estimator of the core will set x = y = 0.
The simplifying assumptions also simplify the CvP error function. With the network parameters {dC, dO, dP, cT}, and the variables {x, y}, the CvP error function becomes:
The components of this simplified CvP error function are best explained using a hypothetical adjacency matrix with an incorrect CP split (Figure 5):
- (1 − dC) (cT − x)2: Errors arising from missing links between the true-core banks placed in the core (in an ideal CP structure, the density of links within the core is equal to one).
- (1 − dO) (cT − x)y: Errors arising from missing links between the true-periphery banks incorrectly placed in the core and the true-core banks placed in the core.
- (1 − dP)y2: Errors arising from missing links between the true-periphery banks incorrectly placed in the core.
- dCx2: Errors arising from links between the true-core banks incorrectly placed in the periphery (in an ideal CP structure, the density of links within the periphery is zero).
- dO(1 − cT − y)x: Errors arising from links between the true-core banks incorrectly placed in the periphery and the true-periphery banks placed in the periphery.
- dP(1 − cT − y)2: Errors arising from links between the true-periphery banks placed in the periphery.
Note: The red lines indicate one possible incorrect CP split
As long as dP > 0, the density of links within any subset of the off-diagonal blocks will be non-zero (as there will be no white shading in Figure 5). As a result, there will be no off-diagonal block errors with any CP split. Allowing for dP = 0 increases the complexity of the error function, so we exclude this unlikely boundary scenario in this section of the paper. Appendix B shows that neither the CvP estimator nor our new estimator permit a core/periphery structure with off-diagonal block errors.
4.4.3 The error-minimising core size
In Appendix B, we prove that for a given c ≥ cT, the value of x that minimises eCvP is x = 0. This means that when the estimated core is at least as large as the true size of the core, no true-core banks will be placed in the periphery. Intuitively, for any c ≥ cT, if a subset of true-core banks is placed in the periphery (i.e. if x > 0), then a subset of true-periphery banks (that is at least as large) must be in the estimated core (recall that c ≡ cT − x + y). But with dC > dO > dP (Assumption 3), the number of errors could be reduced by switching the true-core banks currently in the estimated periphery with some of the true-periphery banks currently in the estimated core (i.e. by setting x = 0 and y = c − cT). Using Figure 5 as an example, this would occur by switching the banks causing errors D and E with the banks causing errors B and C.
Using the same intuition (with proof in Appendix B), for a given c < cT, all the banks that make up the estimated core must be true-core banks (i.e. y = 0). But since c < cT, some true-core banks must also be in the periphery; so x = cT − c > 0 in this scenario.
With the optimal values of x and y determined for any value of c, the error-minimisation problem reduces to one with a single variable (c). Graphically, the CvP estimator sorts the banks so that the shading of the adjacency matrix will look like the right panel of Figure 4 (as opposed to Figure 5), all that is left to determine is where to place the red lines. From this point, the result depends on the values of the parameters {dC, dO, dP, cT} (the results below are proved in Appendix B):
-
When the densities of links in the true-core (dC) and true off-diagonal blocks (dO) are sufficiently small relative to the true size of the core (cT), the CvP estimator underestimates the true size of the core.
- With dC > dO > dP, moving true-core banks into the periphery (i.e. setting c < cT) increases both the density of links within the periphery block and the size of the block; so the number of errors from this block increases. But it also reduces the size of the core block, thereby reducing the number of errors from within the core block (the density of errors within the core block does not change). When dC and dO are sufficiently small relative to cT, the reduction in errors from the core block more than offsets the increase from the periphery block, causing the CvP estimator to underestimate the size of the core.
-
When the densities of links in the true-periphery (dP) and true off-diagonal blocks (dO) are sufficiently high relative to the true size of the core, the CvP estimator overestimates the true size of the core.
- The intuition is analogous to the previous scenario. When dP and dO are sufficiently high and some true-periphery banks are placed in the core, the fall in the number of errors coming from the periphery block more than offsets the increase in the number of errors coming from the core block, causing the CvP estimator to overestimate the size of the core.
- In between these two scenarios, the CvP estimator accurately estimates the size of the core.
To be precise, the CvP error-minimising core size is:
What this means, practically, is that if the density of the network is large (small) relative to the true proportion of banks in the core, the CvP estimator will tend to overestimate (underestimate) the size of the core. Moreover, this inaccuracy will worsen the further the density of the network deviates from the true proportion of banks in the core. This occurs because networks with these properties are expected to generate a large number of errors in one of the blocks, but the CvP estimator does not account for this and instead offsets these errors by changing the size of the core.
5. The Density-based Estimator
The inaccuracy of the CvP estimator results from a focus on the number of errors rather than the density of errors. In Section 4.4, incorrectly classifying banks increases the density of errors in one of the diagonal blocks (i.e. the core or periphery block) and leaves the density of errors in the other diagonal block unchanged. But with some parameterisations this move reduces the total number of errors, so the move is optimal for the CvP estimator.
To overcome this problem, we construct a new estimator that focuses on the density of errors within each block (henceforth, the density-based, or DB, estimator). We do this by dividing each error block in the CvP error function (Equation (3)) by the number of possible errors within that block.[20] Therefore, the DB estimator is the CP split that minimises the following error function:
With the simplifying assumptions from Section 4.4, the global optimum of the density-based estimator is c = cT (see Appendix B for the proof).
The intuition behind this result is as follows. Setting y > 0 causes the density of the core block to fall, and either has no effect on the density of the periphery block (if x = 0) or causes it to increase (if x > 0).[21] Therefore, y > 0 cannot be optimal. Similarly, setting x > 0 causes the density of the periphery block to increase, while either reducing the density of the core block (if y > 0) or leaving it unchanged (if y = 0). Therefore, x > 0 cannot be optimal.
This result does not depend on the values of the network parameters {dC, dO, dP, cT}. Therefore, with the simplifying assumptions, increasing the expected number of errors (i.e. increasing dP or decreasing dC) has no effect on the DB estimator. To determine the accuracy of the DB estimator when the simplifying assumptions are removed, we turn to numerical simulations.
6. Numerical Analysis of Core/Periphery Estimators
Sections 4.4 and 5 assess inaccuracy when the network consists of a continuum of representative true-core banks and a continuum of representative true-periphery banks. Moreover, these sections only evaluate the CvP and DB estimators. To evaluate the performance of all four of the previously discussed estimators, and to assess inaccuracy when networks have a finite number of non-representative banks, we conduct a numerical analysis.
To perform our numerical analysis, we construct 10,000 random draws from a distribution of ‘feasible’ networks. From Section 3, the average number of active banks in our quarterly data is around 40, and the average network density is 0.25. So we restrict feasibility to be networks with N = 40 banks and a density of d = 0.25. We then evaluate the performance of the estimators for various possible true-core sizes (i.e. we construct 10,000 draws for each true-core size).
We incorporate noise by allowing the densities of links within the true-core and true-periphery blocks to randomly deviate from their ideal densities. However, we do not want these densities to deviate so far from an ideal CP structure that the CP model becomes inappropriate; so we impose dC > dO > dP (consistent with Section 4.4). With quarterly networks aggregated from high-frequency data, noise is more likely to come in the form of additional links rather than missing links; so we restrict the noise in the true-core block to be less than the noise in the true-periphery block (i.e. 1 − dC < dP).[22] Once the densities of each block are determined, links are assigned based on an Erdős-Rényi model.[23] Appendix D details the process for constructing simulation draws.
With 40 banks, the number of potential CP splits is 240 = 1 099 511 627 776 (each of the 40 banks is either a core bank or a periphery bank). So it is not feasible to search through all possible partitions to find the global optimum of each estimator. Instead, for each estimator and for each draw from the distribution of feasible networks, we construct 20 random starting points and run a ‘greedy algorithm’ to find the local optimum associated with each starting point.[24] As a result, each estimator's performance will depend on both its theoretical properties and on how easy it is for the greedy algorithm to find a global optimum.
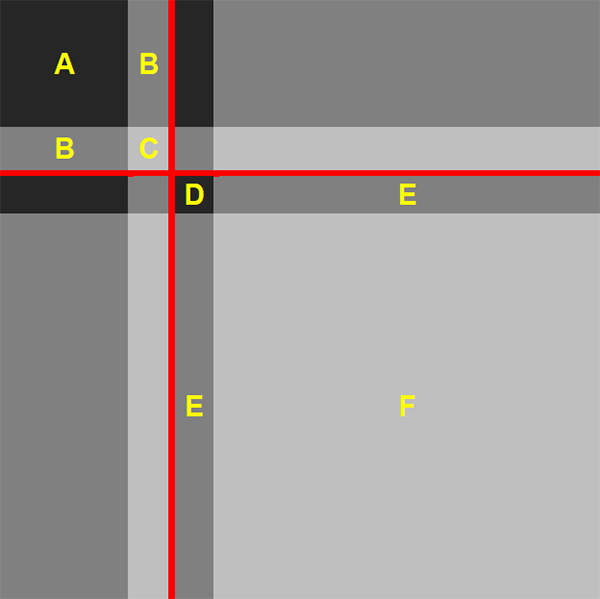
Figure 6 shows the number of banks incorrectly classified by each estimator.[25] The top panel shows the results when there are no missing links in the true-core block (dC = 1), the bottom panel shows the results when missing links are allowed within the true-core block (dC < 1). Even if an estimator accurately determines the size of the core, if it puts the wrong banks in the core then it will register a positive error in this figure.
When the true size of the core is small, the DB estimator is the most accurate; especially given that the noise is added in a way that advantages the maximum likelihood estimator. The relative accuracy of the DB estimator at small core sizes is even higher when looking at the 95th percentiles. At larger core sizes, the DB estimator is slightly less accurate than the other estimators, with the accuracy differential becoming more acute when noise is added to the true core. So no estimator is unambiguously the best, which is problematic given that the true-core size and the volume of noise in real-world networks are unknown.
That said, the accuracy differential when the true core is large is never as high as the differential when the true core is small. And the areas under the DB estimator's error curves in Figure 6 are much lower than the areas under the other estimators' error curves (for both the averages and 95th percentiles).[26] Therefore, the DB estimator is the superior estimator when no prior information about the true size of the core is available.
Figure 7 shows how the estimated core sizes relate to the true-core sizes (on average). Adding noise to the true-core block (bottom panel) magnifies the average underestimate exhibited by the DB estimator at larger true-core sizes. An underestimate occurs when some true-core banks have a sufficiently small number of links (relative to the other true-core banks) that moving them into the periphery reduces the core error-density by more than it increases the periphery error-density. This is more likely to occur when there are fewer links within the true core (i.e. when the amount of noise in the true-core block increases).
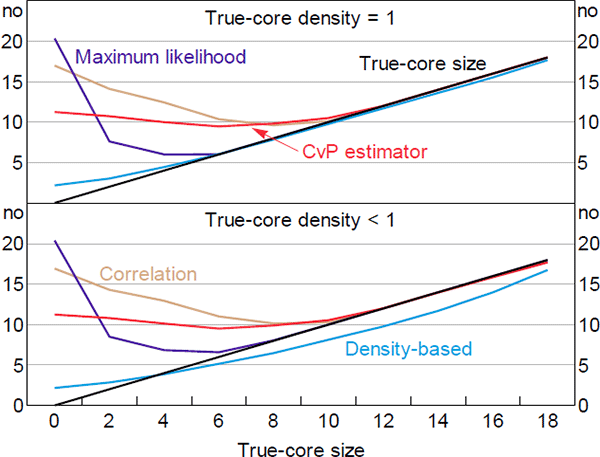
Importantly, the bias exhibited by the DB estimator is relatively stable across true-core sizes. So our DB estimator is likely the best method for evaluating changes in the size of the core over time.
With respect to the CvP estimator, these numerical results are consistent with the theoretical results of Section 4.4. First, the CvP estimator is theoretically inaccurate when the density of the network is high relative to the true size of the core; in the simulations the network density is fixed, so this occurs at small true-core sizes. Second, the inaccuracy is theoretically worse the further the density of the network deviates from the true proportion of banks in the core; in the simulations this translates into the inaccuracy worsening as the true-core size decreases, which is what we observe.
Given the superior performance of our estimator in both these numerical simulations and the earlier theoretical analysis, we use the DB estimator for our analysis of the Australian overnight interbank market.
7. The Core/Periphery Structure of the IBOC Market
7.1 Estimated Core
Figure 8 shows IBOC market core size estimates for every quarter in our sample using three of the estimators evaluated above.[27] As expected, the DB estimator finds a smaller core than the other estimators. Notably, with respect to the CvP estimator, the core found by the DB estimator is much smaller, while that found by the correlation estimator is generally larger. Based on our numerical analysis in Section 6, this suggests that the true-core size is in a region where the DB estimator is likely the most accurate.
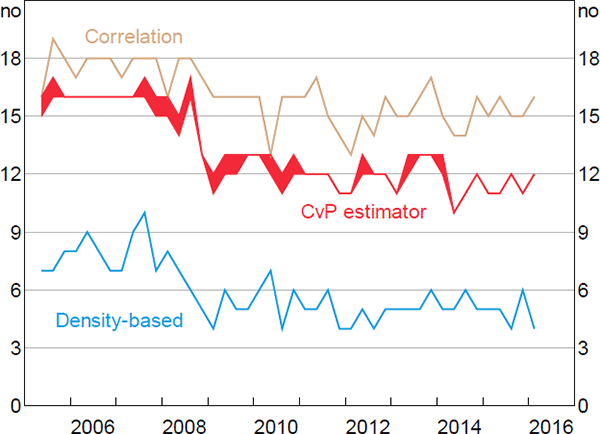
Note: Shaded ranges indicate that our optimisation algorithm found multiple core sizes that optimise the relevant function
The most notable feature of Figure 8 is the fall in the estimated core size that occurred during the 2007–08 financial crisis. Although the size of the fall differs between estimators, all estimators suggest that the typical core size fell during this period.
Based on the DB estimator, the average core size was around eight banks prior to the peak of the crisis (i.e. the average until 2008:Q3) and around five banks afterwards. As expected, the four major banks were almost always estimated to be in the core, both before and after the crisis (Figure 9).
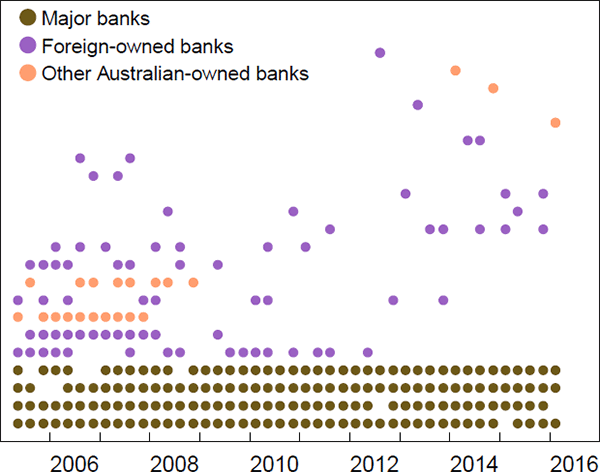
Notes: Each row is a different bank, for which a dot is placed in every quarter that the bank is in the core; the rows are sorted by the frequency each bank is in the core; banks are not identified to preserve confidentiality
Four of the non-major banks that were often in the core prior to the crisis (i.e. those in rows 6, 7, 9, and 10 in Figure 9) were almost never estimated to be in the core after the crisis. Only one of these banks became inactive (an Australian-owned bank), while the other three (one Australian-owned and two foreign-owned banks) moved from the core to the periphery.
Of these banks that moved to the periphery, their average in-degrees (borrowing links) and out-degrees (lending links) all decreased after the crisis. For two of these three banks (one foreign-owned and one Australian-owned), their average number of borrowing links fell more than 80 per cent between pre- and post-crisis, including a reduction in their borrowing links with the remaining core. This reduction in borrowing links was the major cause of them dropping out of the core. For the other bank, the fall in lending links was the major cause of it dropping out of the core; the average number of this bank's lending links fell more than 80 per cent between pre- and post-crisis.
These falls in the number of in- and out-degrees could be due to either/both supply or demand. Using the foreign-owned banks as an example:
- the increased perceived risk of foreign-owned banks during the crisis may have reduced the willingness of some banks to lend to these foreign-owned banks (supply) – consistent with the theoretical models of Freixas and Jorge (2008) and Acharya, Gromb and Yorulmazer (2012); and/or
- the increased stress in the foreign-owned banks' home markets may have prompted their pullback from intermediating in the Australian market (demand).
Unfortunately, the nature of our data does not allow us to determine whether the reductions in degree, and therefore the fall in the core size, are demand or supply driven. What we can conclude, however, is that crises can have long-lasting effects on the IBOC market, and that not all relationships remain reliable during times of stress. Identifying the causes of these banks' reductions in degrees is left for future research.
International studies find both reductions and increases in core size during the crisis. For the Italian overnight market (excluding foreign banks), and using the CvP estimator, Fricke and Lux (2015) find a reduction in the size of the core – from 28 per cent of active banks to 23 per cent. Conversely, Wetherilt et al (2010) find that the core size in the UK overnight market increased during the crisis. They suggest that the UK experience could be due to banks wanting to diversify their borrowing relationships to ensure they could source liquidity even during periods of high stress, or that changes to the UK's reserves management regime may have allowed banks to increase their activity in this market.
7.2 The Changing Relationship between Core and Periphery
In addition to looking at changes in the make-up of the core, we also want to see whether the relationships between the core and periphery changed during the crisis.
Since the ideal CP structure only requires the off-diagonal blocks to be row and column regular, changes in the densities of these blocks (beyond some minimum density) have no effect on the DB estimator. Therefore, looking at changes in the densities of the off-diagonal blocks may provide useful information about changes in the relationships between the core and the periphery.
However, the typical density measure of each off-diagonal block (i.e. the number of links within the block as a proportion of the number of possible links) may be misleading. This is because changes in the composition of the core and periphery may change the density of the off-diagonal blocks, even if none of the banks actually changed their behaviour.[28] As a result, it is difficult to interpret raw changes in the density of the off-diagonal blocks.
To overcome this problem, we construct a ‘density index’. In particular, we consider only banks that are in the same position in consecutive periods; that is, they are either in the core for two consecutive periods or in the periphery for the same two periods. We then compute the growth in the densities of the relationships between these banks and between the two periods, and use these growth rates to construct our index (Figure 10).
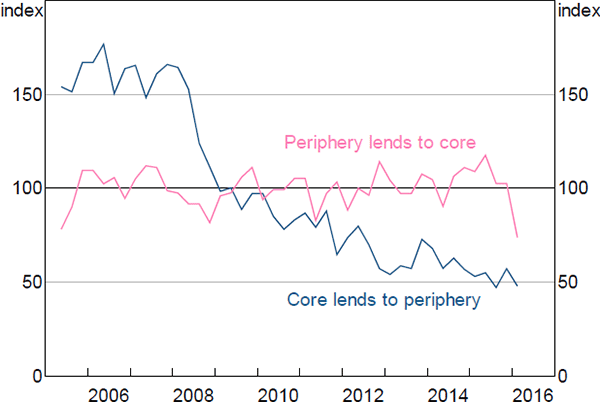
During 2008, the density of the ‘core lends to periphery’ links fell by 40 per cent – the largest year-on-year fall in our sample – and continued to trend down following the crisis (Figure 10). Conversely, the density of ‘periphery lends to core’ links fell slightly during the crisis, but remained around its long-run average in subsequent years.[29]
These trends are consistent with the increased perceived risk that occurred during the crisis. That is, while it is likely that the core banks were perceived as safe, the periphery banks may not have been. So it is plausible that, in such an environment, the core might reduce their exposure to the periphery, with each periphery bank potentially only able to borrow from the core banks with which they have the strongest relationships, if at all.
However, to fully understand the changing relationships between the core and periphery, we must look at lending volumes, not just the number of lending relationships. Although aggregate lending remained elevated during the crisis (Figure 1), there was a large shift in the direction of lending volumes between the core and periphery (Figure 11).[30]
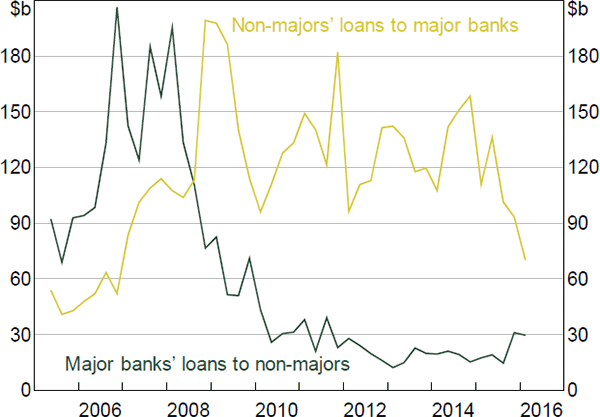
To the extent that, prior to the crisis, periphery banks relied on the core banks for their liquidity, if the core stopped providing this liquidity (or the periphery banks feared that they would), the periphery banks would need to source this liquidity from elsewhere (e.g. the RBA's open market operations, the secured lending market, or term funding markets).[31] The resulting changes in the flows between the core and periphery are consistent with the model of Ashcraft et al (2011). In their model, banks that fear a liquidity shortage desire large precautionary deposit balances. Being precautionary, these banks do not expect to need all of the extra liquidity and therefore expect to have a surplus of funds. As their daily liquidity needs unfold (i.e. as the trading day draws to a close and the need for precautionary balances fades), they seek to lend any excess balances in the market. Knowing this, the core banks reduce their demand for liquidity from other sources, expecting to be able to fund any deficit by borrowing from the periphery.
Our findings are consistent with those of other overnight interbank markets. In the Italian market, the financial crisis led to a reduction in the density of ‘core lending to periphery’ links, no clear difference in the density of ‘periphery lending to core’ links, a reduction in core-to-periphery lending volumes, and an increase in periphery-to-core lending volumes (Fricke and Lux 2015). In the UK market, the densities of both off-diagonal blocks fell during the crisis (Wetherilt et al 2010).
As the acute phase of the crisis passed, demand for precautionary balances by the periphery likely waned (Figure 11). However, the data suggests periphery banks never returned to their pre-crisis reliance on the core for their liquidity. Therefore, in addition to having a long-lasting effect on the core/periphery structure of the IBOC market, the crisis has also had a long-lasting effect on the relationships between the core and periphery.
8. Conclusion
This paper has both a theoretical and an empirical contribution. For our theoretical contribution, we evaluated the accuracy of several commonly used estimators of core/periphery network structures and found them to be highly inaccurate in networks that have either a relatively large or relatively small core. This is particularly problematic because the core is what we are trying to determine, so the extent of the inaccuracies is typically not known a priori.
We analytically derive the source of this inaccuracy, and derive a new estimator – the density-based estimator – that is designed to overcome this problem. In numerical simulations, our estimator outperformed the commonly used estimators.
For our empirical contribution, we applied our density-based estimator to the IBOC market. We found that the 2007–08 financial crisis had a large and long-lasting effect on the market: the core shrank; the remaining core reduced their exposure to the periphery; and the periphery switched from being net borrowers to net lenders (consistent with models of precautionary liquidity demand).
One possible explanation for these long-lasting effects is that it may be less costly for the periphery to preserve their current lending relationships than to let these relationships lapse and try to renew them in a future crisis. Moreover, to the extent that there are fixed costs associated with large changes in market dynamics, it is possible that another large shock would be required for the market to revert to its previous state. Determining why temporary changes can have long-lasting consequences for the structure and functioning of interbank markets is left for future research.
From an operational perspective, there are two important conclusions. First, that we should not be complacent if the IBOC market's structure seems robust to shocks, because some of these relationships may quickly evaporate during periods of stress. And second, that temporary shocks can have long-lasting implications for the market. This is important not only for predicting the effect of future crises, but also for determining the effect of any operational changes (i.e. even temporary changes in the RBA's operations may have a long-lasting effect on this market).
Appendix A : The Maximum Likelihood Estimator
Partition the N × N adjacency matrix (A) into four blocks: the core lends to core block, the core lends to periphery block, the periphery lends to core block, and the periphery lends to periphery block. Assuming the links in each block come from an Erdős-Rényi random network, the probability mass function for a link in block i is a Bernoulli distribution (with support k ∈ {0,1} and probability pi):
Since each link in an Erdős-Rényi network is independent, the joint probability function of all the links in the adjacency matrix is the product of N(N − 1) Bernoulli distributions:
where si is the number of possible links in block i and λi is the number of actual links in block i. With each bank's designation as core or periphery determining the composition of the four blocks, the joint probability distribution is defined by N + 4 parameters (the designations of the N banks, and the four pi parameters).
Both si and λi depend on the matrix A and on the core/periphery partition, but not on the probability pi. Therefore, we can determine the maximum likelihood estimator of pi conditional on the data and the core/periphery partition in order to produce a concentrated log-likelihood function where the only unknown parameters are whether each node is in the core or the periphery.
The conditional maximum likelihood estimator of pi is λi/si. However, for our analysis it is handy to concentrate-out the λi parameter so that the concentrated log-likelihood function becomes:
where pi is now a function of the data and the core/periphery partition via the relationship λi = sipi.
For a given core/periphery partition, the log-likelihood has the same value if the designation of every bank is switched (i.e. every core bank becomes a periphery bank and every periphery bank becomes a core bank). Therefore, the maximum likelihood estimator requires the identifying restriction pCC ≥ pPP (where i = CC is the block of core lends to core links and i = PP is the block of periphery lends to periphery links).
Since pi ∈[0,1], each component of the sum in Equation (A1) is bounded above by zero.[32] This upper bound occurs when either pi = 0 or pi = 1. Since pi = λi/si, the upper bound for each component is reached when either no links exist in the corresponding block or all the links in the block exist. Therefore, if we ignore the components of Equation (A1) that correspond to the off-diagonal blocks, the true CP split of an ideal CP network produces the largest possible value of the likelihood function.
Appendix B : Estimator Accuracy
B.1 Accuracy of the Craig and von Peter (2014) Estimator
Reproducing Equation (4):
If we fix c, and then substitute out y through the identity y ≡ c − cT + x, then for a given core size the derivative of the error sum with respect to x is:
Since dC > dO > dP (Assumption 3), the above derivative is greater than zero. Therefore, for any given core size, the error-minimising value of x is its smallest possible value. Given the identity y ≡ c − cT + x, this means x = 0 if c ≥ cT and x = cT − c if c < cT (since y ≥ 0). Using these values for x, the error sum can be written such that the only variable is c. Differentiating eCvP with respect to c then gives:
With Assumption 3, dCcT + dO(1 − cT) > dOcT + dP(1 − cT). Therefore, the above derivative at any point in the c < cT region is lower than at any point in the c ≥ cT region. Combined with the fact that 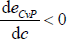 when c = 0 and
when c = 0 and 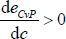 when c = 1, there is a unique global minimum for eCvP. This unique global minimum depends on the parameter values in the following way:
when c = 1, there is a unique global minimum for eCvP. This unique global minimum depends on the parameter values in the following way:
B.1.1 Error-minimising core size when dP = 0
When dP = 0, off-diagonal block errors are possible. However, it requires both true-periphery banks to be incorrectly placed in the core (i.e. y > 0) and all true-core banks to be in the core (i.e. x = 0); if x > 0 then every row/column subset of the off-diagonal blocks will have a non-zero density (see Figure 5). In this boundary scenario, the CvP error function becomes:
Differentiating with respect to y gives:
Therefore, the error function with off-diagonal block errors is bounded below by (1 − dc)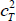 . But this is the value of the CvP error function when x = 0 and y = 0. So the CvP estimator will never set x = 0 and y > 0 when dP = 0, and there will never be any off-diagonal block errors with the CvP estimator.
. But this is the value of the CvP error function when x = 0 and y = 0. So the CvP estimator will never set x = 0 and y > 0 when dP = 0, and there will never be any off-diagonal block errors with the CvP estimator.
B.2 Accuracy of the Density-based Estimator
With the simplifying assumptions in Section 4.4, the error function of the DB estimator becomes (i.e. dividing each block in Equation (4) by the number of possible errors within that block):
Differentiating the error function with respect to x and y gives:
Since dC > dO > dP (Assumption 3), the above derivatives are positive for all feasible x and y (i.e. values that ensure c ∈(0,1)). Therefore, the error function is minimised when x = y = 0. This means that c = cT is the core size that minimises the DB error function.
B.2.1 Error-minimising core size when dP = 0
Dividing each block in Equation (B1) by the number of possible errors within that block gives:
Differentiating with respect to y gives:
Therefore, the error function with off-diagonal block errors is bounded below by 1 − dC. But this is the value of the DB error function when x = 0 and y = 0. So the DB estimator will never set x = 0 and y > 0 when dP = 0, and there will never be any off-diagonal block errors with the DB estimator.
Appendix C : The Two-step Cucuringu et al (2016) Estimator
Cucuringu et al (2016) propose a two-step process for estimating the core/periphery split of a network. The first step uses some criteria to rank the nodes by ‘coreness’. Cucuringu et al propose several ranking criteria, including ranking nodes by their degree. Given this ranking, the second step then chooses where to draw the line between core and periphery.
The second step uses an error function similar to our DB estimator. The main differences are that missing links in the off-diagonal blocks are all treated as errors (rather than just requiring row or column regularity), and that they put bounds on the possible core sizes. While these bounds can be set to the bounds of the network (i.e. [0, N]), Cucuringu et al find that their two-step estimator performs poorly without more restrictive bounds.[33]
The upside of their process is that it is potentially more efficient. For any given ranking, determining the CP split requires evaluating at most N + 1 possible splits (i.e. possible core sizes from zero to N). If the first step also requires only a small number of calculations (e.g. ranking based on degree), then an optimisation algorithm for the Cucuringu et al (2016) estimator will be much faster than our DB estimator (with either a global search (2N possible CP splits) or a greedy algorithm with multiple starting points).
However, if the global optimum is not one of the CP splits over which the second step searches, the Cucuringu et al (2016) estimator cannot find the global optimum. So the Cucuringu et al estimator is, at best, only as accurate as our DB estimator with a global search. While this result may not hold when using a greedy algorithm with the DB estimator, the performance of the Cucuringu et al estimator will always be bounded by the quality of the first-step ranking.
To give an example of the problem, we ran the Cucuringu et al (2016) estimator on simulated data constructed using a method similar to the one outlined in Section 6 (Figure C1). In this simulation, we set dC = 1 and dO = dP; this is done not for realism but to highlight the potential extent of the problem. For simplicity, we rank nodes by their degree as the first step.[34] And to highlight the issues associated with the two-step procedure (as opposed to differences resulting from the different error functions), we adjust the error function used in the second step to match Equation (5).
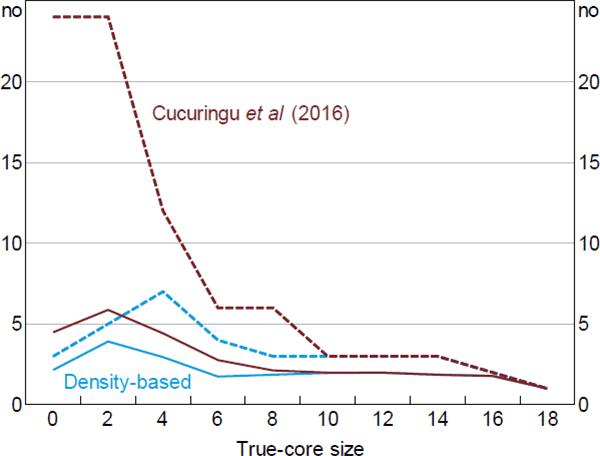
Note: The version of the Cucuringu et al (2016) estimator used here ranks nodes by their degree as the first step, and adjusts the second step to be consistent with the Craig and von Peter (2014) definition of a core/periphery structure
When the true-core size is large, the Cucuringu et al (2016) estimator performs as well as the DB estimator. This is expected since it is when the true-core size is large that ranking nodes by their degree is more likely to be an accurate measure of their ‘coreness’. When the true-core size is small, the Cucuringu et al estimator exhibits a larger average error than the DB estimator. The difference between estimators is starker when comparing the tails of their error distributions, with the 99th percentile from the Cucuringu et al estimator being comparable to the worst-performing estimators in Section 6.
Interestingly, Cucuringu et al (2016) also find that a second-step error function that focuses on the number of errors (i.e. one akin to the CvP estimator) often leads to ‘disproportionately-sized sets of core and peripheral vertices [nodes]’ (p 856). But they provide no explanation of the reason. Our theoretical analysis fills this gap.
Appendix D : Process for Constructing Simulation Draws
The simulations that allow missing links within the true-core block require the imposition of three inequality constraints on the densities of the true-core, true-periphery and true off-diagonal blocks. The simulations then draw randomly from all possible networks that satisfy these constraints. As discussed in Section 6, the inequality restrictions are:
- dC > dO
- dO > dP
- 1 − dC < dP
For simulations that do not allow missing links within the true-core block, dC = 1 and the first and third inequality restrictions become obsolete.
Imposing these restrictions is based on the following identity (cT is the true size of the core):
The left-hand side is the number of links in the simulated network, which is known since we parameterise the simulations based on the observable average size and density of the networks formed from our data. The right-hand side decomposes this into the links in each block (when the banks are split into the true core and true periphery).
To impose the third restriction, we draw r from unif(0, 1) and set dC = (r – 1)dP + 1 (for simulations in which dC = 1, we set r = 1). Substituting this into Equation (D1) then gives us a linear relationship between dO and dP (since {d, N, cT, r} are already parameterised), which we can then use to impose the other inequality restrictions.
To ensure dP > 0 (required by definition of a ‘density’):
Note that dN(N − 1) − cT(cT − 1) >0 with our parameterisations.
To ensure dO > dP:
To ensure dC > dO, the relevant inequality depends on the values of the other parameters. If the following holds:
then the relevant inequality is (the numerator is always positive with our parameterisations):
If Equation (D4) does not hold, then Equation (D5) is not necessary.
Denote the left-hand sides of Equations (D2), (D3) and (D5) as UB1, LB, and UB2, respectively. Then if Equation (D4) holds, dO is drawn from unif(LB, min{UB1, UB2}). If Equation (D4) does not hold, dO is drawn from unif(LB, UB1).
Finally, substituting dC = (r − 1)dP + 1 and the draw for dO into Equation (D1) gives the draw for dP, which is then substituted into dC = (r − 1)dP + 1 to give the draw for dC.
With the densities of each block drawn, the locations of the links within each block are determined using an Erdős-Rényi model (ensuring the off-diagonal blocks retain the necessary row/column regularity).
Appendix E : Results with Higher-frequency Networks
Our baseline results are based on networks constructed at a quarterly frequency. Here we discuss the robustness of our findings to changes in the aggregation period. Specifically, we apply our density-based estimator to unweighted–directed networks constructed at monthly and weekly frequencies.
As expected, the shorter the horizon of time aggregation, the smaller the network size and its density. The average number of active banks on a given week (month) in our sample is 34 (37), as opposed to an average of 41 active banks for each quarter. The average weekly (monthly) density is 0.11 (0.19), as opposed to 0.25 on average in our quarterly networks.
Figure E1 shows the time-varying core sizes for the weekly and monthly aggregation periods. At the monthly frequency, we estimate the typical pre-crisis core size to be 4–5 banks, falling to 3–4 banks post-crisis. Therefore, the fall in core size that we find in our baseline analysis is still visible in the monthly data, albeit with a smaller core. The weekly networks show no discernible change in core size between pre- and post-crisis.
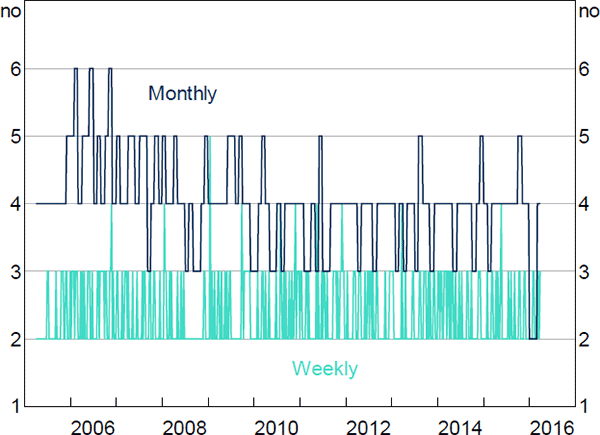
The divergence we find between aggregation periods is not unusual. Finger, Fricke and Lux (2012) compare the network properties of the Italian interbank loans market across daily, monthly, quarterly, and yearly frequencies and conclude that inference based on high-frequency aggregation periods may be misleading. In particular, they ‘show that the networks appear to be random at the daily level, but contain significant non-random structure for longer aggregation periods’. This is because high-frequency networks ‘provide probably only a very small sample of realizations from a richer structure of relationships’ (Finger et al 2012).
Appendix F : Evidence of Intermediation
In the core/periphery model proposed by Craig and von Peter (2014), one of the key features of the core is that they intermediate the lending/borrowing of the periphery banks. In the ideal core/periphery structure, this intermediation results in the core banks having both lending and borrowing links with the periphery. However, while observing such links is a necessary condition for this ideal intermediation, it is not sufficient, especially with low-frequency networks.
For example, suppose we split the network into large and small banks. By virtue of their size, the large banks may have relationships with many small banks. On some days, a given large bank may have a surplus of funds while some small banks have a deficit; so this large bank may lend to the small banks. On other days, the reverse may occur, causing the large bank to borrow from several small banks. When aggregated to a quarterly frequency, this behaviour would be observationally equivalent to intermediation. Moreover, if the small banks only had relationships with the large banks, and the large banks also borrowed from/lent to each other, the quarterly networks would resemble a core/periphery structure.
Even though the large banks are not intermediating in this example – since they are only lending/borrowing based on their own requirements – the fact that the small banks only deal with the large banks makes the large banks ‘core’ to the system. So one could argue that such a network still exhibits a core/periphery structure. That said, we want to present evidence that the core banks in our networks are actually intermediating.
To do this, we look at the share of days in which each bank both lends and borrows in the IBOC market (Figure F1). The average share is much higher for the core banks than it is for the periphery banks, supporting our claim that the core banks are intermediating in the IBOC market.
We note, however, that banks may also borrow and lend on the same day due to forecast errors.[35] If the distribution of forecast errors is symmetric, and banks have no tolerance for forecast errors, we would expect both core and periphery banks to exhibit a share of 50 per cent in Figure F1. Therefore, the difference between the core and periphery banks could just be due to differing tolerances for forecast errors.[36]
That said, Hing, Kelly and Olivan (2016, p 37) state that ‘most banks wait until they are reasonably certain of their liquidity position … before transacting in the cash [IBOC] market’. And, over the sample period, the average shares for each of the major banks (as these banks are almost always in the core) are statistically higher than 50 per cent (at the 1 per cent level). So they likely represent more than just forecast errors.
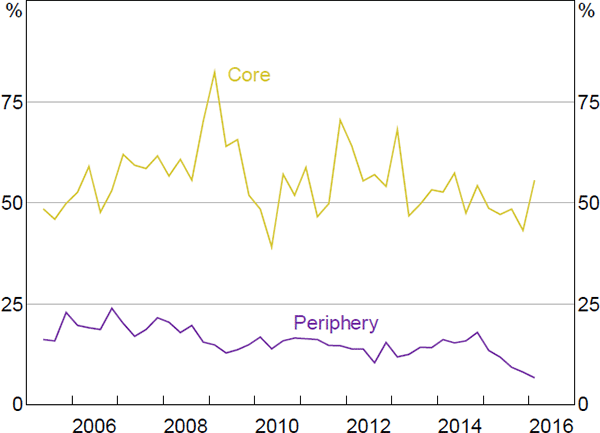
Note: Simple average of banks' quarterly share
References
Acharya VV, D Gromb and T Yorulmazer (2012), ‘Imperfect Competition in the Interbank Market for Liquidity as a Rationale for Central Banking’, American Economic Journal: Macroeconomics, 4(2), pp 184–217.
Albert R and A-L Barabási (2002), ‘Statistical Mechanics of Complex Networks’, Reviews of Modern Physics, 74(1), pp 47–97.
Allen F and D Gale (2000), ‘Financial Contagion’, Journal of Political Economy, 108(1), pp 1–33.
Anufriev M and V Panchenko (2015), ‘Connecting the Dots: Econometric Methods for Uncovering Networks with an Application to the Australian Financial Institutions’, Journal of Banking & Finance, 61(Supplement 2), pp S241–S255.
Ashcraft A, J McAndrews and D Skeie (2011), ‘Precautionary Reserves and the Interbank Market’, Journal of Money, Credit and Banking, 43(s2), pp 311–348.
Bech ML and E Atalay (2010), ‘The Topology of the Federal Funds Market’, Physica A: Statistical Mechanics and its Applications, 389(22), pp 5223–5246.
Borgatti SP and MG Everett (2000), ‘Models of Core/Periphery Structures’, Social Networks, 21(4), pp 375–395.
Boss M, H Elsinger, M Summer and S Thurner (2004), ‘Network Topology of the Interbank Market’, Quantitative Finance, 4(6), pp 677–684.
Boyd JP, WJ Fitzgerald and RJ Beck (2006), ‘Computing Core/Periphery Structures and Permutation Tests for Social Relations Data’, Social Networks, 28(2), pp 165–178.
Brassil A, H Hughson and M McManus (2016), ‘Identifying Interbank Loans from Payments Data’, RBA Research Discussion Paper No 2016-11.
Chapman JTE and Y Zhang (2010), ‘Estimating the Structure of the Payment Network in the LVTS: An Application of Estimating Communities in Network Data’, Bank of Canada Working Paper 2010-13.
Chiu J and C Monnet (2016), ‘Relationships in the Interbank Market’, Bank of Canada Staff Working Paper 2016-33.
Copic J, MO Jackson and A Kirman (2009), ‘Identifying Community Structures from Network Data via Maximum Likelihood Methods’, The B.E. Journal of Theoretical Economics, 9(1).
Craig B and G von Peter (2014), ‘Interbank Tiering and Money Center Banks’, Journal of Financial Intermediation, 23(3), pp 322–347.
Cucuringu M, P Rombach, SH Lee and MA Porter (2016), ‘Detection of Core-Periphery Structure in Networks Using Spectral Methods and Geodesic Paths’, European Journal of Applied Mathematics, 27(6), pp 846–887.
Della Rossa F, F Dercole and C Piccardi (2013), ‘Profiling Core-Periphery Network Structure by Random Walkers’, Scientific Reports, 3, Article No 1467.
Finger K, D Fricke and T Lux (2012), ‘Network Analysis of the e-MID Overnight Money Market: The Informational Value of Different Aggregation Levels for Intrinsic Dynamic Processes’, Kiel Institute for the World Economy, Kiel Working Paper No 1782.
Freixas X and J Jorge (2008), ‘The Role of Interbank Markets in Monetary Policy: A Model with Rationing’, Journal of Money, Credit and Banking, 40(6), pp 1151–1176.
Fricke D and T Lux (2015), ‘Core–Periphery Structure in the Overnight Money Market: Evidence from the e-MID Trading Platform’, Computational Economics, 45(3), pp 359–395.
Furfine CH (1999), ‘The Microstructure of the Federal Funds Market’, Financial Markets, Institutions & Instruments, 8(5), pp 24–44.
Garvin N, D Hughes and J-L Peydró (forthcoming), ‘Interbank Repo and Unsecured Markets during the Crisis’, RBA Research Discussion Paper.
Haldane AG (2009), ‘Rethinking the Financial Network’, Speech given at the Financial Student Association, Amsterdam, 28 April.
Hing A, G Kelly and D Olivan (2016), ‘The Cash Market’, RBA Bulletin, December, pp 33–41.
in ′t Veld D and I van Lelyveld (2014), ‘Finding the Core: Network Structure in Interbank Markets’, Journal of Banking & Finance, 49, pp 27–40.
Langfield S, Z Liu and T Ota (2014), ‘Mapping the UK Interbank System’, Journal of Banking & Finance, 45, pp 288–303.
Martinez-Jaramillo S, B Alexandrova-Kabadjova, B Bravo-Benitez and JP Solórzano-Margain (2014), ‘An Empirical Study of the Mexican Banking System's Network and its Implications for Systemic Risk’, Journal of Economic Dynamics and Control, 40, pp 242–265.
Tellez E (2013), ‘Mapping the Australian Banking System Network’, RBA Bulletin, June, pp 45–53.
van der Leij M, D in ′t Veld and C Hommes (2016), ‘The Formation of a Core-Periphery Structure in Heterogeneous Financial Networks’, De Nederlandsche Bank Working Paper No 528.
Wetherilt A, P Zimmerman and K Soramäki (2010), ‘The Sterling Unsecured Loan Market during 2006–08: Insights from Network Theory’, Bank of England Working Paper No 398.
Zhang X, T Martin and MEJ Newman (2015), ‘Identification of Core-Periphery Structure in Networks’, Physical Review E, 91(3).
Acknowledgements
We thank Chris Becker, Matt Boge, Adam Gorajek, David Olivan, Valentyn Panchenko, John Simon, and participants of seminars at the BIS, ECB, Kiel University, RBA, RBNZ, University of NSW, and University of Padova for advice and suggestions. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia. The authors are solely responsible for any errors.
Footnotes
The interconnectedness of the Australian financial system has previously been studied using different data sources. Tellez (2013) analyses Australian banks' large exposures, while Anufriev and Panchenko (2015) estimate interconnectedness from partial correlations between entities' equity returns. Network analyses have been conducted for international interbank markets (see Bech and Atalay (2010) and Wetherilt, Zimmerman and Soramäki (2010), for example), but not for the IBOC market. [1]
Examples include Craig and von Peter (2014) for Germany, Wetherilt et al (2010) and Langfield, Liu and Ota (2014) for the United Kingdom, in ′t Veld and van Lelyveld (2014) for the Netherlands, Martinez-Jaramillo et al (2014) for Mexico, and Fricke and Lux (2015) for Italy. [2]
In any real-world analysis, the model used does not capture everything that influences the data (with the external influences treated as ‘noise’). For example, two banks that would otherwise only interact with the core may also have a direct relationship that developed from their other operations (i.e. outside the IBOC market). Such an idiosyncratic relationship would be noise when trying to identify any core/periphery structure. [3]
Although some non-banks are able to participate in the IBOC market, the majority of participants are banks. For simplicity, this paper refers to all participants as ‘banks’. [4]
From May 2016, the RBA has required banks to identify every IBOC loan when it is entered into the RBA's settlement system. [5]
The four major Australian banks are Australia and New Zealand Banking Group Limited, Commonwealth Bank of Australia, National Australia Bank Limited and Westpac Banking Corporation. Confidentiality requirements prevent us from identifying individual banks. [6]
For the same reason, much of the literature applying core/periphery models to interbank markets focuses on unweighted networks (e.g. Wetherilt et al 2010; Craig and von Peter 2014). [7]
While this model is designed to work with undirected networks, it can be applied to directed networks by using the model to construct either the in-degrees or the out-degrees (with the other degrees forming mechanically as a result of this process, but not necessarily with the same degree distribution). [8]
Where C is a constant ensuring the probabilities sum to one. [9]
Power law degree distributions are scale free because the probability of any degree is equal to the scaled probability of any other degree. That is, P(X = ak) = a−γP(X = k) where a is a positive constant. [10]
Our networks differ from many other real-world networks that appear to be scale-free (Albert and Barabási 2002), including the large-exposures networks of the Australian banking system (Tellez 2013) and the Austrian interbank market (Boss et al 2004). [11]
Quarterly networks aggregated from high-frequency data can exhibit features that are observationally equivalent to the features produced by intermediation, but are actually caused by the aggregation process. In Appendix F we use the high-frequency data to provide evidence that the tiering structure exhibited in our quarterly networks actually reflects intermediation. [12]
Row (column) regularity means that each row (column) in the block must contain at least one non-zero element. [13]
The CP model can be adjusted to consider each node as having some amount of ‘coreness’. This is done for weighted networks in Borgatti and Everett (2000) and Fricke and Lux (2015), and for both weighted and unweighted networks in the random-walker model of Della Rossa, Dercole and Piccardi (2013), for example. We do not consider these alternatives because these models do not allow any structure to be placed on the off-diagonal blocks, and would require the imposition of an arbitrary coreness cut-off to determine which banks are in the core and how the size of the core has changed over time. [14]
While our paper is the first to assess the relative performance of these estimators, in ′t Veld and van Lelyveld (2014, p 33) mention that with the estimator they use the ‘relative core size is closely related to the density of the network’ and that ‘one should therefore be careful not to take the core size too literally’. [15]
Since these sets do not incorporate the off-diagonal blocks of the adjacency matrices, this method does not require an ideal core bank to be an intermediary. [16]
Variations of the maximum likelihood estimator are also used in the literature, see Chapman and Zhang (2010) and Zhang, Martin and Newman (2015), for example. [17]
We follow Wetherilt et al (2010) and include the off-diagonal blocks in the likelihood function. This improves the performance of the maximum likelihood estimator in the numerical analyses conducted in Section 6. We note, however, that in small samples the theoretical implications of including the off-diagonal blocks in the likelihood function are not clear. [18]
Craig and von Peter (2014) actually minimise a normalisation of this error sum. However, this normalisation is invariant to the CP split, so it can be ignored for our purposes. [19]
Cucuringu et al (2016) recently derived a similar estimator independently of Craig and von Peter (2014). There are, however, some important differences between our DB estimator and the estimator proposed by Cucuringu et al, with the theoretical performance of their two-step estimator being no better than our one-step estimator. This is discussed in Appendix C. [20]
Recall that x is the share of banks that are true-core banks but are placed in the periphery, and y is the share of banks that are true-periphery banks but are placed in the core. [21]
For a pair of banks, a link occurs if there is at least one loan during a quarter, a missing link only occurs if there is never a loan during the quarter. [22]
This advantages the maximum likelihood estimator that has this as a parametric assumption. Using another network model to introduce noise is akin to imposing a probability distribution on the residual in a linear regression model. [23]
From a given starting point, a greedy algorithm searches through all possible single changes (i.e. changing a single bank from core to periphery, or vice versa) and determines the change that optimises the function (i.e. it does not account for future changes). It then makes this change and repeats the process until there is no single change that can improve the function (i.e. it finds a local optimum).
When our algorithm finds multiple CP splits that minimise the relevant error function (different starting points may lead to different local optima that produce the same error function value), it randomly chooses the estimated CP split from among these options.
We ran the same analysis using 200 random starting points on 1,000 random draws. The results were unchanged.
[24]
A periphery bank being classified as a core bank is an incorrect classification, as is a core bank being classified as a periphery bank. [25]
The exception is the 95th percentile curves when dC < 1, where the smallest area is 46 (CvP estimator) while the area under the density-based curve is 47. [26]
We do not document the results based on the maximum likelihood estimator as it produced core size estimates that were more volatile and larger (on average) than the estimates produced by any of the other three estimators. The maximum likelihood estimator results are available upon request. [27]
For example, suppose all banks remaining in the core had fewer relationships with the periphery after the crisis than they had before the crisis. If the banks that dropped out of the core had a lower-than-average number of links with the periphery (before the crisis), the densities of the off-diagonal blocks may actually increase during the crisis. [28]
In 2008:Q3, our optimisation algorithm for the DB estimator found two CP splits with the minimum error. The core size is the same with both splits, but the alternate split attenuates the 2008 fall in the ‘core lends to periphery’ index (to 32 per cent) while amplifying the fall in the ‘periphery lends to core’ index. The only other quarter where multiple error-minimising splits were found was 2015:Q4. [29]
Figure 11 splits the system into the major banks and non-major banks because the major banks are estimated to be in the core throughout the sample period. It would also be possible to construct a ‘lending volumes index’ for the core and periphery in the same way as the density indices in Figure 10, but this would remove information about relative volumes. [30]
Garvin, Hughes and Peydró (forthcoming) show that as perceived risk increased during the crisis, banks with weak fundamentals and plentiful collateral increased their secured borrowing more than other banks. [31]
Evaluating xlnx when x = 0 as its limit value as x → 0 (to prevent the log-likelihood from being undefined at the bounds of pi). [32]
Since our DB estimator does not require any bounds, the need for more restrictive bounds could be due to their two-step procedure. [33]
While Cucuringu et al (2016) provide ranking criteria that may be more accurate, the point of this exercise is to show the potential extent of the problem, not to evaluate the best version of their estimator. [34]
Banks' need for the IBOC market arises from the tens of thousands of payments that flow between banks on a daily basis. Any error in forecasting these flows could result in a bank lending (borrowing) too much, requiring them to borrow (lend) to offset their forecast error. [35]
For example, if the typical values of forecast errors for some banks are sufficiently small, it may be more profitable for these banks to maintain a small liquidity buffer than to retain sufficient staff for late-day re-entry into the IBOC market. [36]