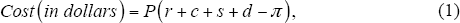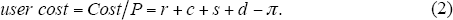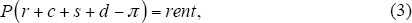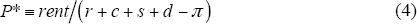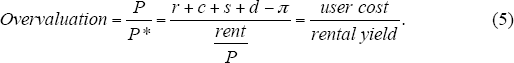RDP 2014-06: Is Housing Overvalued? 3. The User Cost of Housing

A comprehensive comparison of the relative costs of owning and renting adds up the discounted costs of each alternative over the period for which a house is expected to be owned. We present and discuss comparisons along these lines in Section 5.4. However, a useful simplification is to compare cash flows and changes in asset values at a point in time.

The annual cost of owning a home can be written as

where P represents the price of the property; r the real interest rate (a composite of the mortgage rate and the opportunity cost of owner's equity); c represents other running costs, such as repairs, rates and insurance, as a proportion of the price; s represents buying and selling costs (stamp duty, agent commission, etc.), also as a proportion of the price, averaged over the period of home-ownership; d is the physical depreciation rate; and π is the expected real appreciation rate of the property on a constant-quality basis (that is, excluding the effects of improvements and depreciation). In contrast to other countries, the Australian income tax code does not directly affect the cost of housing for owner-occupiers. The nearest exception is local government rates, which we include in running costs. Our division into five components is for presentational convenience. In Appendix A we show a decomposition with many more elements.

It is convenient to express the annual cost as a percentage of the value of the property, which we will refer to as the user cost:

A household is financially as well off owning as renting if

where prices, rents and other terms are measured for similar properties. Under assumptions we discuss and relax below, both sides of the equation can be assumed to be approximately constant over the period of ownership.

Equation (3) implicitly defines a ‘fundamental’ value for housing, P*, at which a household is financially as well off buying or renting.

Equation (4) is similar to the widely-used Gordon model of share price valuation, which compares the corporate earnings (or dividend) yield to the risk-free interest rate and other related terms. In analysing share prices it is common to assume that expected prices represent a solution to the same problem, but we follow other papers in the housing literature, which treat expected capital gains as separately determined. Equity pricing equations typically include a risk premium, which we discuss in Section 5.3.

P/P* represents a measure of overvaluation, which, after re-arranging terms, can conveniently be expressed as the ratio of the user cost to the rental yield:

The equations above involve several simplifications. First, they ignore changes in the user cost over the period of home ownership. That is not a concern if all flows are constant, which is a reasonable assumption for most variables if they are measured in real terms.^[4] If measured in nominal terms, rents would be expected to rise in line with inflation, though the nominal interest payments on a loan would not. Strictly speaking, flows cannot be constant if there is real capital appreciation, which involves changing relative prices. It would be more accurate to allow for changing relative prices, to replace π with π / (1 + r), discount the selling cost component of transactions costs, and so on. But these complications do not greatly matter, as we show in Section 5.4.

Second, we assume that government programs that influence the cost of home ownership, such as First Home Owners Grants or the exemption of housing from some means tests, are small enough to be ignored.

A more important simplification is that we take rent and expected capital appreciation as exogenous. This approach, standard in the literature cited in Section 2, is partial and may seem inconsistent: the household is assuming that future home buyers solve a different problem to that being considered here. A more complete treatment would explain rents and expected appreciation within a model of the demand and supply of housing, as noted in the introduction. Assuming that expectations are consistent with that model would simplify the analysis, but would also make it difficult to discuss bubbles.

Footnote

In Australian data, variations in the growth of real rents have been small. This contrasts with the growth in corporate earnings, which is volatile and difficult to predict. So whereas research on equity valuation often solves for the expected growth in earnings, estimates of housing valuation can assume expected rental growth is given. [4]