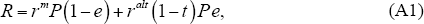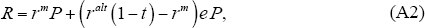RDP 2014-06: Is Housing Overvalued? Appendix A: Data Details
July 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 1.14MB
This appendix discusses our data in detail so as to permit readers to understand, extend and vary our estimates. We also explain why our data choices differ from those others have made. As a roadmap, Table A1 shows a breakdown of components of the user cost in April 2014, assuming expected capital appreciation equals the historical mean. Essentially, this is column 1 of Table 1 in more detail.
| Total | ||
|---|---|---|
| (Table 1 entry) | ||
| Average 10-year fixed mortgage rate | 7.5 | |
| less term premium | 1.3 | |
| equals average expected mortgage rate | 6.2 | |
| less expected inflation | 2.8 | |
| equals Real interest rate (r) | 3.3 | |
| Council rates | 0.3 | |
| plus repairs | 0.3 | |
| plus depreciation on plant | 0.3 | |
| plus body corporate fees | 0.2 | |
| plus water | 0.1 | |
| plus insurance | 0.1 | |
| plus other running costs | 0.2 | |
| equals Running costs (c) | 1.5 | |
| Stamp duty | 4.0 | |
| plus conveyancing and other buying costs | 0.3 | |
| equals total buying costs | 4.3 | |
| Real estate agent commission | 2.5 | |
| plus advertising, legal and other selling costs | 0.5 | |
| equals total selling costs | 3.0 | |
| Total transaction costs | 7.3 | |
| Average (over ten years) transaction costs (s) | 0.7 | |
| Depreciation of structure (d) | 1.1 | |
| Change in real median house price (1955–2014) | 3.1 | |
| less alterations and additions (1961–2005) | 1.1 | |
| less high quality/size of new houses | 0.9 | |
| plus depreciation | 1.1 | |
| plus change in location | 0.4 | |
| equals Change in constant-quality prices (π) | 2.4 | |
| Total user cost (r + c + s + d – π) | 4.2 | |
| Average rental yield (rent / P) | 4.2 | |
Overvaluation as per cent of fundamental value  |
0 | |
| Note: Components may not add exactly to totals due to rounding | ||
A.1 Rental Yields
Since 2010, the RBA has commissioned RP Data-Rismark, a private property data provider, to compile estimates of the average ratio of rents to prices of matched properties.[7] These estimates have been regularly published by the RBA in its Statement on Monetary Policy and other Bank publications. The numerical data are confidential and available for purchase from RP Data.
For each of the eight capital cities and a national composite we have separate estimates for houses and units. The numerator in each of these estimates equals the sum of annual advertised rent on all properties listed for rent on major real estate websites. These websites cover almost all properties available for rent. The denominator is the sum of imputed prices on those same properties. Imputed prices are a weighted average of two components. The first is the most recent sale price of the property, multiplied by the change in a hedonic price index over the period since that sale. This component receives a weight that declines as the period since the sale increases, reaching zero at ten years. The second component is the prediction of hedonic regressions – that is, the average price at that time for a unit or house in that postcode with the same floor size, bedrooms, bathrooms and other observable characteristics. Sales on nearby properties are given a higher weight in these calculations. The RP databases (like the APM data used by Hill and Syed (2012)) are unusual in that they match administrative data on sale prices with detailed property characteristics from internet advertisements for a near-universal sample.
Each quarter, about 100,000 advertised rents and the same number of imputed prices enter the rental yield calculation, with houses typically slightly outnumbering units. Details on the hedonic indices and regressions are in Hardman (2011a, 2011b, 2013).
Imputed prices differ slightly from sale prices due to random variation. The regression standard error is about 8 per cent, which might be considered to be reasonably accurate. However, for our purposes what matters is the within-sample mean. By construction, the average imputed price equals the average sale price. Characteristic-specific dummies mean this holds at a highly disaggregated (such as postcode) level. It is possible that rental properties systematically differ in price from owner-occupied properties (and hence from average sale prices) in ways that are not captured by the hedonic regressions. Discussions with real estate agents suggest this is unimportant; consistent with this, previous occupancy status is rarely mentioned in advertisements. In any case, it would be captured in the valuation for those properties where a recent sale is recorded.
Figure A1 shows some estimates of rental yields. Our preferred series is labelled as ‘RP Data-Rismark (rental properties)’. The series labelled ‘RP Data-Rismark (all properties)’ represents slightly different estimates that RP Data publish on their website, which impute rental yields to the total dwelling stock (rather than just properties advertised for rent). The RBA has chosen to emphasise the estimates for rental properties as being more accurate and conceptually simpler. For other purposes, the estimates for all properties might be more representative, though the difference is small.
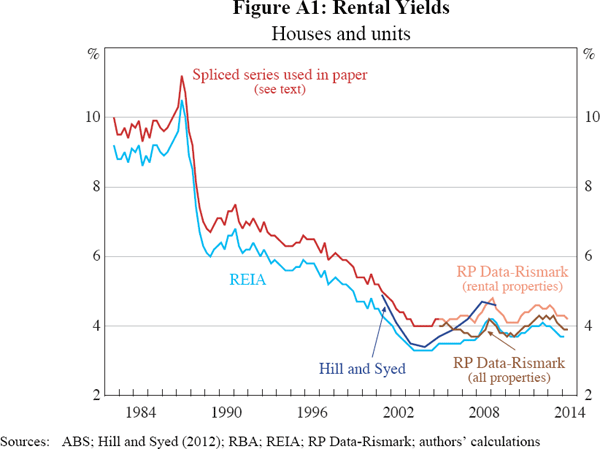
Because the RP Data–Rismark estimates compare prices and rents for properties of the same quality, they are a dramatic advance on the estimates used by most previous researchers discussed in Section 2, permitting a much broader set of questions to be meaningfully examined. They are quite similar to the estimates of Hill and Syed (2012), which we also show in Figure A1, and, in method of construction, to the estimates of Davis et al (2008) for the United States. Our estimates differ from those of Hill and Syed in several respects, though whether these differences matter may depend on the purpose. Hill and Syed's estimates are publicly documented in considerably greater detail, including their sensitivity to alternative assumptions. Whereas Hill and Syed's estimates are for Sydney houses, the RP Data-Rismark estimates we use are for all capital city dwellings. The RP Data-Rismark estimates benchmark imputed prices to past sale prices for the property; and, importantly for the purposes of the RBA, they are timely, with a one month publication lag.
The RP Data–Rismark estimates have some limitations. Advertised rents will differ from actual rents; for example, if subsequent adjustments do not equal changes in market rates. Furthermore, using advertised properties means that we weight rental yields by turnover and time on market. This may be unrepresentative of the rental stock in general if properties with unusually high rents are listed for longer or have higher turnover. Hill and Syed (2012, footnote 8) and conversations with real estate agents suggest that these biases are not important.
A more important, practical limitation of the RP Data-Rismark rental yield estimates is that they are only available in consistent form back to 2005. Before then, we splice on estimates from the Real Estate Institute of Australia (REIA) of median rents and median dwelling prices. As noted above, the median dwelling is a more expensive property than the median rental. So the rental yield constructed from REIA estimates is lower than the rental yield from matched properties. Compositional changes will affect the REIA estimates over time, though it is not clear whether these biases are important, or even whether they are positive or negative. For example, the trend increase in the share of unit rentals will impart a downward bias, whereas the increased density of rentals in city centres will impart an upward bias. In the hope that such biases are approximately offsetting, we splice the RP Data-Rismark estimates with level-adjusted REIA estimates to extend the time series back from June 2005 to September 1982.
For Section 6 we require separate estimates of prices and rents. We measure prices using RP Data-Rismark's hedonic all capital cities dwelling series, and multiply this by the rental yield estimates above to obtain rents.
A.2 Expected Appreciation
The appropriate assumption for expected capital gains will depend on the purpose of the analysis. To examine whether home buyers behave rationally or predictably, a measure of actual expectations is relevant. There are several surveys of house price expectations in Australia, of which the NAB survey of property professionals, discussed in Section 7.1, is probably the most direct. Surveys by Westpac-Melbourne Institute and Mortgage Choice show similar movements, but are harder to summarise as a point estimate. The NAB survey estimates have limitations. Respondents are asked about expectations over the next two years, but it is unclear whether they report a sum or an average. Accordingly we report the one-year-ahead estimate, even though most capital gains will be realised at much longer horizons. We do not know how representative the respondents' answers are: home buyers may have different expectations to property professionals. Incentives to develop and report accurate expectations are weak. We do not know how these reported expectations have changed over time. We do not know how respondents define ‘house prices’; for example, whether they include improvements or depreciation. Studies in the United States (see Case, Shiller and Thompson (2012) and accompanying comments) suggest that many home buyers have difficulty answering survey questions in a sensible or consistent manner.
To measure overvaluation, or to decide on whether to buy a house, the appreciation rate that should be expected is relevant. If one assumes expectations are rational, or has faith in the wisdom of crowds, this would coincide with actual expectations, which the NAB and other surveys attempt to measure. But for those sceptical of survey responses, a statistical approach may provide a better guide.
Stapledon (2007, 2012) has constructed a long time series for median house prices, based on advertisements, sales notices and other primary sources. We have updated this series following his methodology. Stapledon argues that there were structural breaks in house prices after World War II, reflecting legislation restricting the supply of land and the lifting of wartime price controls. But since then, median house values have followed a clear upward trend, rising at an annual rate of 3.1 per cent in real terms from 1955 to 2014. We follow Stapledon's choice of a break point of 1955. Stapledon estimates that over most of this period (1960–2005), expenditure on alterations and additions contributed 1.15 percentage points a year to average house values, the higher quality and size of new houses contributed 0.87 percentage points, and depreciation detracted 1.06 percentage points. The increased distance of the average house from city centres detracts 0.35 percentage points. Applying these adjustments to the 1955–2014 period, the price of a house of constant quality would have increased at an annual average rate of 2.4 per cent.
Stapledon's estimates are attractive for our purposes because of their long time span and because they are measured consistently with other components of the user cost. In contrast, alternative price measures would require adjustments to our user cost definition. For example, repeat sales indices such as Residex in Australia or the Federal Housing Finance Agency and CoreLogic indices used in US research, include improvements and depreciation. To estimate the user cost consistently would then require including the cost of improvements and removing the cost of depreciation, though other authors do not always make these adjustments. More problematic are stratified and hedonic price indices, the scope of which is ambiguous. For example, these measures do not explicitly remove the effect of depreciation, though it is correlated with characteristics that are controlled for. Hence, measuring house price appreciation using a stratified index (as Hill and Syed (2012) do) or a hedonic index (as we do in our house price decomposition in Section 6) would give rise to partial double-counting.
A.3 Depreciation
We use Stapledon's (2007) estimate that depreciation of structures subtracted an average 1.06 per cent per year from house values from 1960 to 2005. This estimate is exactly offset by a positive adjustment to expected capital appreciation on a constant-quality basis, so does not affect estimates of the user cost or overvaluation. A seemingly simpler alternative might be to ignore this term and assume that prices include the effects of wear and tear. We prefer to make an explicit adjustment for depreciation for consistency with other researchers and with other data, such as on rents.
Stapledon's estimate is lower than Hill and Syed's (2012) assumption of 2.5 per cent, which is based on US studies. It is also well below the Australian Tax Office's (ATO) allowable depreciation rate of 2.5 per cent which applies to the value of the structure, whereas Stapledon's applies to the value of the property. About two-thirds of the value of residential real estate reflects land and location.
The share of structures in property values has declined substantially over time. One might think that this would imply a declining contribution from depreciation. However, for reasons that are not clear, this is not evident in Stapledon's estimates.
A.4 Interest Rate
A.4.1 Choice of interest rate
The average discounted variable interest rate on new home loans is shown as the purple line in Figure A2. An alternative series, the average interest rate on all housing loans, is very similar but includes fixed interest rates on old loans, which are not relevant to current decisions. (Though the latter series does have the advantage of longer availability.) The average discounted variable rate is currently 5.1 per cent, about 85 basis points below the widely cited ‘standard variable rate’ used by the OECD (2005) in its estimates of overvaluation.
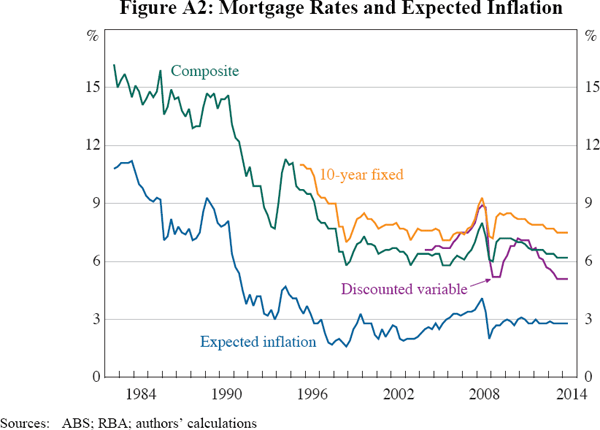
Although most Australian home loans are at variable interest rates, these rates are an imperfect guide to the average interest rate that will prevail over a period of home ownership, which is the measure we are interested in. The reason is that they are subject to large temporary fluctuations. When variable rates are unusually low, as they are in 2014, they are typically expected to increase over the medium to longer term. Under the expectations theory of the term structure, the average variable interest rate should approximately equal a long-term fixed interest rate, such as the average 10-year fixed mortgage rate, also shown in Figure A2.
There are two problems with data on 10-year fixed mortgage rates. First, the data are thin, with few loans being made at this rate. However, in itself, this does not make the series unrepresentative. The 10-year interest rate appears to move closely and predictably with more popular mortgage rates. Our results would not be markedly different were we to use a more common rate, smoothed in line with the yield curve.
The more important, though related, problem is that long-term fixed interest rates include a substantial term premium. As can be seen in Figure A2, the average 10-year fixed mortgage rate is usually well above the average variable interest rate on new loans. From 2004 to 2014 this difference averaged 126 basis points. That sample is short, however, term premiums measured using closely related interest rates over longer time periods are similar. Most borrowers neither need nor choose to pay this premium. Housing loans at fixed rates only constitute a small share of total loans – their share has fluctuated around 10 per cent over the past decade – with most of these being fixed for three years or less.
Our approach is a blend of these measures, labelled ‘composite’ in Figure A2. From 1995 through to the present, we use the 10-year fixed interest rate, from which we subtract 126 basis points, the average term premium. For the period in which both original data series are available, our composite series is constructed so as to have the same average level as the average discounted variable rate on new loans and the same variability as the fixed rate. Our data on 10-year fixed mortgage rates goes back to 1995. We extend this back to 1982 (when our rental yield data begins) by splicing it with the 10-year government bond yield. This approach assumes that the margin between expected mortgage rates and bond yields did not change in this earlier period. That seems a reasonable assumption for the period 1989 to 1995, given that 5-year fixed mortgages moved in line with 5-year bonds. Earlier data are difficult to interpret but do not clearly point to a change in expected margins.
A.4.2 The opportunity cost of equity
Interest payments comprise two elements. The first is the interest on the mortgage, which we denote as the product of the mortgage rate, rm, and the size of the loan. Let the share of the property that is equity be e, then the size of the loan is the product of the value of the property, P and (1 − e). The second component is the equity in the house, which has an opportunity cost – it could be earning (taxable) interest if it was invested elsewhere. Denote this cost as ralt, the interest rate on alternative assets, and the tax rate on these earnings as t. The sum of these terms is given by
which can be rewritten as
where the first term represents the level of interest rates and the second term is an interest differential effect. Our baseline estimates assume this interest differential term is zero. We view this assumption as a) simple, b) central and c) a reasonable approximation for many home buyers. However, evidence for these properties, particularly the third, is not strong.
Assuming the interest differential effect is zero most obviously applies to those for whom equity, e, is small, such as first home buyers and others with little investible financial wealth. Those for whom ralt(1 − t) exceeds rm, that is, those who have attractive alternative investments and for whom paying off a mortgage is an inferior method of saving, might also be expected to have little equity. Conventional wisdom might suggest this group is small: paying off the mortgage is commonly recommended as a sensible investment priority. However, that advice assumes the investor already owns a house, in which case paying off a mortgage is a risk-free investment. But for examining the decision as to whether to rent or buy, that assumption does not apply. Acquiring a mortgage is complementary with buying a house, an investment that involves large financial risks. For that decision, the relevant alternative investment is risky, such as shares. The real pre-tax return to equities in Australia has averaged 6.9 per cent since 1979 [8] or 7.3 per cent since 1883 (Brailsford, Handley and Maheswaran 2008, Table 1), well above the expected real mortgage rate, currently about 3.3 per cent. Moreover, investing in an equity index is more liquid and less risky than the leveraged purchase of an undiversifiable house. Taxes complicate this comparison but it is not clear that they change it much.[9]
Of course, not everyone pays the average interest rate. Households with few financial assets pay more: they are charged mortgage insurance and they borrow at high rates, for example on credit cards, more frequently. Conversely, households with substantial financial savings, especially those that exceed superannuation thresholds, may believe their opportunity cost is low. Explanations of the cross-section distribution of home ownership would need to take these variations into account.
A.5 Transactions Costs
Large one-off outlays are incurred when buying or selling a home. The largest of these is stamp duty. Estimates from state revenue offices suggest this has risen from about 2 per cent of property values in 1980 to about 4 per cent of the value of the property currently. The rate is usually higher on expensive properties, and varies between investors, first home buyers and other owner-occupiers, complications we ignore. Our assumption differs from the series presented by Stapledon (2007, Figure 4.11), which includes stamp duty paid by investors and commercial real estate. Conveyancing costs (about $700 to $2,500) are perhaps the next largest cost, followed by loan origination fees, buyer's agent fees, inspection costs and so on (Home Purchase Advisory Service 2010). All up, we assume that buying costs add about 4¼ per cent to the current purchase price of a property. We ignore First Home Owners Grants and stamp duty concessions: rough calculations suggest that these measures may have reduced buying costs (averaged across all buyers) by about 1 percentage point at their maximum, though typically by much less.
The main element of selling costs is the real estate agent's commission, which discussions with industry contacts suggest has declined slightly over time, and now averages about 2½ per cent of the sale price, or slightly less in the large cities. Advertising, legal, financial and administrative fees may add a further ½ per cent.
In total, we assume that buying and selling costs now add about 7¼ per cent to the cost of a property. We assume that they added slightly more, on net, in the past: our assumptions for changes over time are simple but unimportant. This needs to be amortised over the period for which the property is owned. According to the ABS's Survey of Income and Housing, the median time spent in a dwelling by owner-occupiers is ten years (Bloxham, McGregor and Rankin 2010, Graph 3). Ten years also happens to be close to the average time between house sales (RP Data 2012) and the horizon chosen by Smith and Smith (2006, p 19) based on US data. A total cost of 7¼ per cent amortised over ten years represents an additional cost to owning a house of 0.725 per cent a year.
Several market participants with whom we have discussed our estimates of buying and selling costs have been surprised at how low they are. That seems to reflect the narrow definition of the estimates rather than problems with the underlying data and assumptions. Our estimates focus on financial costs and exclude the time and effort involved. These costs are implicitly included within the rental premium. We exclude repairs and cleaning costs, which we explicitly include under ‘running costs’, and we exclude moving costs, which would be incurred whether one owned or rented.
A.6 Running Costs
Other costs of home ownership can be grouped under the heading of running costs. Our estimates of running costs are based on expenses that landlords claim as deductions against their income tax. Table A2 summarises data from the ATO's 2010/11 Taxation Statistics – Individual Tax. We present these as a share of total rental income and, assuming an average rental yield of 4.2 per cent in 2010/11, as an annual percentage of property value.
| As a per cent of: | ||
|---|---|---|
| Rental income | Property value | |
| Expenses also incurred by owner-occupiers | ||
| Council rates | 7.2 | 0.3 |
| Repairs and maintenance | 6.3 | 0.3 |
| Plant depreciation | 6.1 | 0.3 |
| Body corporate fees | 5.0 | 0.2 |
| Water charges | 3.3 | 0.1 |
| Insurance | 2.9 | 0.1 |
| Sundry rental expenses | 2.8 | 0.1 |
| Borrowing expenses | 0.8 | 0.0 |
| Cleaning expenses | 0.6 | 0.0 |
| Gardening/lawn mowing expenses | 0.5 | 0.0 |
| Pest control | 0.2 | 0.0 |
| Legal fees | 0.1 | 0.0 |
| Subtotal | 35.8 | 1.5 |
| Extra expenses incurred only by investors | ||
| Property agent fees/commission | 6.3 | 0.3 |
| Land tax | 2.2 | 0.1 |
| Travel expenses | 1.2 | 0.1 |
| Advertising for tenants | 0.2 | 0.0 |
| Stationary, telephone and postage | 0.2 | 0.0 |
| Subtotal | 10.1 | 0.4 |
| Expenses for which we use other data | ||
| Interest on loan(s) | 75.3 | 3.2 |
| Capital works | 6.2 | 0.3 |
| Subtotal | 81.5 | 3.5 |
|
Note: Components may not add exactly to subtotals due to rounding Sources: ATO, Taxation Statistics, Individuals' Tax, Individuals' tax detailed tables, Table 15: Rental property schedules; authors' calculations |
||
We assume that many of the expenses landlords claim – shown in the top section of Table A2 – are representative of what owner-occupiers would also expect to pay, on average. The largest of these are council rates (7.2 per cent of rents), repairs and maintenance (6.3 per cent), and depreciation of plant (6.1 per cent). In total, these expenditures constitute 35.8 per cent of rental income or 1.6 per cent of the value of the average rental property.
For comparison, the second section of Table A2 shows running costs that investors would expect over and above the expenses incurred by owner-occupiers, such as property agent fees (6.3 per cent of rents) and land tax ( 2.2 per cent). The third section of the table shows deductions that are claimed by landlords which we include elsewhere and, hence, do not include within our category of running costs. These are interest costs (discussed in Section A.4) and depreciation of structures and other capital works (discussed in Section A.3).
We use the estimates of running costs that would be incurred by owner-occupiers for the period for which it is available, 2005/06 through 2010/11. Over this period it was stable at about 36 per cent of rental income. The broader category of landlord expenses excluding interest and capital works is available back to 1992/93. Over this period this category has been a stable 48 per cent of rents, though a declining share of property value. On this basis, we extrapolate our estimates of running costs back from 2005/06 as 36 per cent of rents. These trends mean that running costs contribute positively to the growth in house prices in the 1990s and early 2000s, with a small negative contribution since then, as shown in Figure 4.
An alternative data source on running costs is the ‘Income from Dwelling Rent’ table in the ABS annual national accounts, used by Stapledon (2007). However, these data include expenses paid by landlords but not owner-occupiers. Another alternative is the ABS Housing Occupancy and Costs (Cat No 4130.0, 2009-10, Table A4, p 94), which has recently been run jointly with the Household Expenditure Survey (HES). Relative to the estimates in Table A2, the HES data imply similar costs for insurance, repairs and maintenance, slightly lower rates, and substantially lower body corporate fees. That may reflect reporting errors or differences in coverage between the two data sources. However, the HES data are harder to extend back in time, due to changes in definitions. Furthermore, their coverage is too narrow for our purposes. For example, expenses such as replacement of household furnishings and equipment which the tax statistics classify as depreciation of plant are classified by the HES as spending on consumer durables and are not separately identifiable.
A.7 Expected Inflation
To present interest rates and expected appreciation in real terms we need a measure of inflation expectations. We use expectations over the next ten years derived from inflation swaps (Finlay and Olivan 2012, Graph 8). As of April 2014, this was 2.8 per cent. Before 2007, we splice this measure with the break-even 10-year inflation rate on indexed bonds. Before 1986, we splice this with a 5-year back-average of the change in the headline CPI. In calculating expected real appreciation rates, we use Stapledon's (2007) historical house price series which are deflated by the chain-weighted price index for household consumption.
Footnotes
We would like to express our gratitude to Tony Richards and Matthew Hardman, who were instrumental in the creation of this series. [7]
Annual geometric mean return on the S&P/ASX 200 Accumulation index (RBA Statistical Table F7 Share Market), deflated by the CPI over 1979–2013. [8]
After imputation, most dividends are taxed at the marginal personal tax rate with nominal capital gains taxed at half this rate. These taxes can be reduced by investing in superannuation, especially via salary sacrifice. Home equity is more liquid than superannuation, however, the marginal benefits of liquidity diminish as wealth increases (that is, for sums that matter). [9]