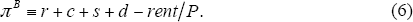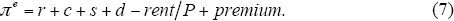RDP 2014-06: Is Housing Overvalued? 5. Estimates
July 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 1.14MB
5.1 Current Estimates
Table 1 shows estimates of parameters and overvaluation for April 2014. In the absence of reliable estimates for π, the expected rate of real appreciation, the table shows two illustrative values of this parameter. We discuss other plausible assumptions in Section 7.1.
| Estimate | ||
|---|---|---|
| Post-1955 expectations | Ten-year average expectations | |
| Real interest rate (r) | 3.3 | 3.3 |
| Running costs (c) | 1.5 | 1.5 |
| Annual average transaction costs (s) | 0.7 | 0.7 |
| Depreciation (d) | 1.1 | 1.1 |
| Expected appreciation (π) | ||
| 1955–2014 average | 2.4 | |
| 2004–2014 average | 1.7 | |
| Total user cost (r + c + s + d − π) | 4.2 | 4.9 |
| Average rental yield (rent / P) | 4.2 | 4.2 |
Overvaluation as per cent of fundamental value  |
0 | 19 |
|
Notes: The bottom row subtracts 1 from Equation (5) to express the degree of overvaluation as per cent of the fundamental value; other variables are defined in the text Sources: see Appendix A |
||
The first column in Table 1 assumes home buyers expect real constant-quality house prices to rise by 2.4 per cent a year, their average rate of increase since 1955. On this assumption, in April 2014, the cost of owning was the same as that of renting, 4.2 per cent of the value of the house. That is, houses are fairly valued.
A long-term average provides a clear, simple reference point. However, many (though not all) forecasters believe that house prices are likely to grow at a somewhat slower rate in the future. An investigation of the merits of different forecasts is outside the scope of this paper. However, to illustrate, we use the average of the past ten years, 1.7 per cent, in the second column. For reasons discussed below, the ten-year average is not a good rule for forecasting prices, however, it currently may be closer to a consensus assumption than the post-1955 average, and it has other advantages, some of which are noted in Section 5.3. On this basis, the annual cost of owning a house would have been 4.9 per cent of the value of the property, 19 per cent greater than the 4.2 per cent cost of renting.
The estimates in Table 1 are our central results, which we restate in Section 8 after considering some variations and technical details.
5.2 Historic Estimates
In deciding whether to buy a house, current estimates of the parameters, as shown in Table 1, are relevant. However, to interpret buyer behaviour and assess the dynamics of the housing market, time series are useful. We expect these historical comparisons to be of direct interest to policymakers but only indirectly to individual home buyers, in so far as it helps them assess the estimates in Table 1.
The three panels of Figure 1 extend entries in Table 1 back in time. In general, we consider our recent data to be good, with the exception of estimates of capital appreciation. As we go back in time, data quality deteriorates. Our estimates at the beginning of our sample are of marginal quality; whereas estimates for earlier periods do not seem worth showing.
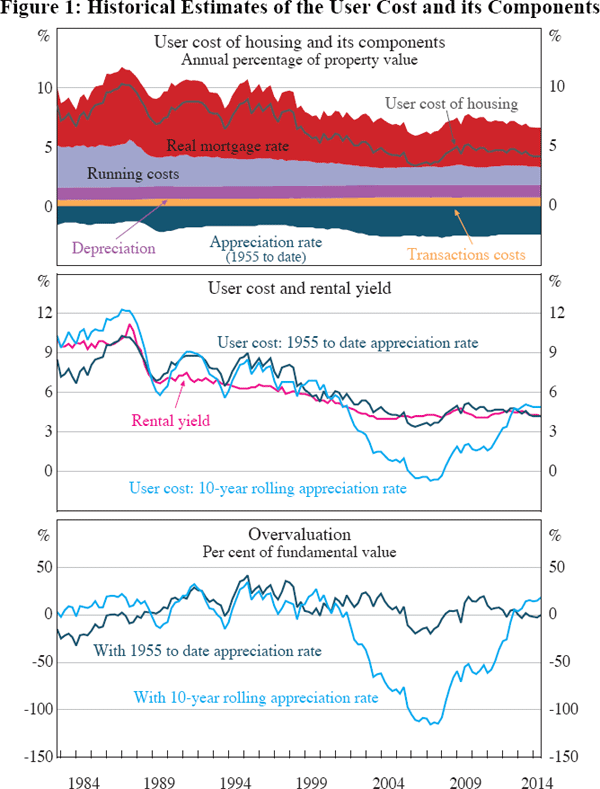
The top panel shows components of the user cost (measured as a percentage of the property value). To reduce clutter, this panel only shows estimates for one proxy for capital appreciation: the average rate of appreciation from 1955 to the date of sale. The middle panel shows (in dark blue) the measure of user costs from the top panel together with the measure that proxies expected appreciation with a 10-year rolling average (in light blue). We also show the average rental yield. The bottom panel shows estimates of overvaluation using the measures of user cost shown in the middle panel. Positive estimates represent overvaluation, that is, the amount that home buyers are paying in excess of what they would pay to rent a similar house.
We make five observations about Figure 1. First, as shown in the bottom panel and discussed further in Section 7.1, estimates of the extent or even direction of overvaluation are sensitive to assumptions about capital appreciation. This point is emphasised in many of the papers mentioned in Section 2.
Second, in contrast to estimates at a point in time, conclusions relating to longer periods are more robust to assumptions about expectations. For both proxies, estimates of overvaluation fluctuate around zero. There has been no clear tendency of Australian houses to be overpriced or underpriced, and the level of overvaluation, when averaged over a long time span, has been small.
An equivalent way of saying this is that the rental yield, on average, is similar to the user cost, as shown in the middle panel. Indeed, if we focus on long-run historical expectations, the relationship between these series is surprisingly close. There is substantial year-to-year volatility, but in the medium term, prices seem well-explained by rents and the user cost. This applies to both levels and changes. More formally, prices, rents and the user cost appear to be cointegrated in logarithms. That implies that measures of overvaluation should be useful for forecasting, though investigating that question is beyond the scope of this paper.
This result has implications for the importance of non-financial factors (an awkward term for factors that may lead one to rent or buy even when the expected financial costs might suggest otherwise). Some households prefer to own than rent because they want security of tenure and the freedom to renovate. Others choose to rent due to risk aversion and limited access to credit. The value of these non-financial considerations can be assessed by the amount that households are prepared to pay for them, represented by the wedge between the rental yield and the user cost. The small size of this wedge, when averaged over time, suggests that the average value of these non-financial considerations has been small. Presumably, the factors that have led some households to rent have been offset by factors that incline other households toward owning. We further discuss (and measure) non-financial considerations in the next section.
Third, as can be seen in the middle panel, the rental yield trends down over our sample. Hence, studies that compare recent levels of this ratio or its inverse to its historic mean, such The Economist (2013) or the OECD (2013), will persistently find large ‘overvaluation’. This downtrend in rental yields has been matched by similar downtrends in the user cost (middle panel), in turn largely reflecting a downtrend in real mortgage rates (top panel). Measures of overvaluation (bottom panel) are trendless.
Fourth, our measures of overvaluation can be compared to others' estimates. Our measure of overvaluation based on long-run expectations shows similar movements to Hill and Syed's (2012, Table 9) preferred measure (with 20-year expectations) for Sydney between 2001 and 2009. Like them, we find prices overvalued in the early 2000s, becoming undervalued in the second half of the decade, then switching back to overvalued following the global financial crisis. More important, we share their assessment that the average deviation from financial fundamentals has been small.
These findings for Australia contrast with results for the United States from studies that also use matched prices and rents. Smith and Smith (2006, Figures 8 and 9), and Garner and Verbrugge (2009, Figure 7) find that US houses have tended to be undervalued by large margins. Smith and Smith's conclusion is disputed by their discussant, Mayer. Although there are many reasons why our results differ from these studies, one important factor is the treatment of expected appreciation, discussed below. As a general observation, these US studies need to be interpreted cautiously given that they find house prices were undervalued near the peak of the US housing boom.
Fifth, a striking feature of the bottom panel is that prices are more than 100 per cent undervalued in 2006 when expectations are proxied by a ten-year average. Over the ten years to 2006, real house price appreciation averaged 6½ per cent a year. This exceeded other components of the user cost, so the total user cost was negative, as shown in the middle panel. Interestingly, Garner and Verbrugge (2009, Figure 7) also estimate negative user costs in the United States at this time, reflecting high expected capital appreciation. Taken at face value, these estimates imply that, given the large capital appreciation, people could expect to live in their house for free. Whether such an expectation is plausible is controversial: in standard models it would imply demand becomes infinite.
We are sceptical of estimates of overvaluation at a point in time where expectations are proxied by a short rolling average. This approach leads to conclusions that housing is undervalued at the peak of the bubble. Nevertheless, this assumption is standard in the literature. Among Australian studies, Brown et al (2011) use a 5-year average, Bourassa and Yin (2006) use a 3-year average, and Hill and Syed (2012) use 10-year and 20-year averages. Similarly, Himmelberg et al (2005) use a 5-year average in the United States, Browne et al (2013) use a 4-year average in Ireland, and Kivistö (2012) uses a 5-year average in Finland. Muellbauer (2012) discusses this issue and suggests using a 4-year average.
5.3 Break-even Appreciation Rates
Because of the difficulties in measuring expectations, an attractive benchmark for assessing home values is the break-even rate of appreciation. If we solve Equation (3) for π, we get the rate of appreciation that makes the financial returns from buying equal those from renting. That is:
This break-even rate is shown as the light blue line in Figure 2.
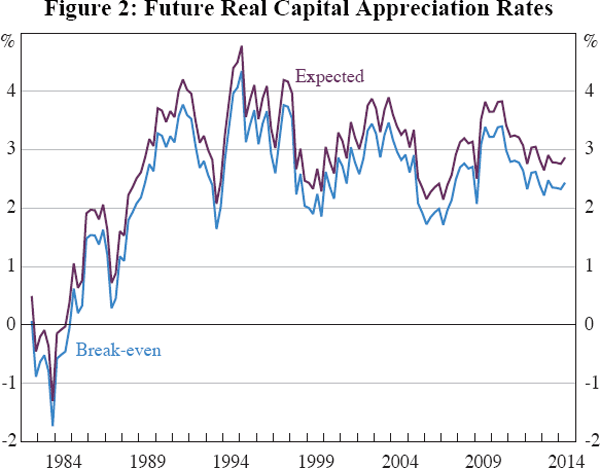
The April 2014 break-even appreciation rate indicates that housing is a profitable investment if real house prices are expected to rise by more than 2.4 per cent per annum. Because it does not require an assumption about expected capital gains, the break-even rate is a clearer and less ambiguous summary measure of our results than the overvaluation ratio. Accordingly, we use it in our sensitivity analysis below. But one should not overstate this benefit, given that it is difficult to assess whether a particular break-even estimate is high or low without some reference to historical appreciation rates. For example, the most recent break-even rate of 2.4 per cent equals the long-run average rate of capital appreciation, (consistent with the estimate of zero overvaluation reported in Table 1), and is somewhat greater than the ten-year average of 1.7 per cent.
Although McCarthy and Peach (2004), Hill and Syed (2012, Section 6.2), and others use the break-even rate as a measure of expectations, it could be biased. A difference in the cost of renting and owning – and hence a difference between the break-even rate and expectations – can be sustained indefinitely if there are non-financial benefits or costs of owning relative to renting. However, it is possible to adjust the break-even rate for these non-financial considerations, and hence reduce the bias. On the assumption that household tastes are fairly stable over time, non-financial benefits can be quantified as the average premium that renters are willing to pay, over and above the cost of home ownership. This rental premium is analogous to premiums paid for risk or liquidity studied in the finance literature.
As discussed in the previous section, non-financial benefits seem to be small, on balance. For either measure of expectations, the financial costs of owning shown in the middle panel of Figure 1 have, on average, been close to the financial costs of renting. To estimate the premium more precisely, we take historical averages as representative of typical returns. That is a strong assumption, but standard in the financial literature and the research cited in Section 2. We also need to make an assumption about a proxy for the expected rate of capital appreciation. For this purpose a rolling ten-year average has several advantages over the post-1955 average. First, it is less susceptible to bias arising from structural breaks. Second, a rolling average weights observations over the sample evenly, whereas the long-run mean overweights the relatively subdued appreciation in the early part of the sample. Third, the ten-year average more closely corresponds to the ex post, or realised, cost of ownership.
On that basis, the annual cost of owning, shown as the light blue line in the middle panel of Figure 1 has averaged 5.8 per cent since 1982. This is about 0.4 percentage points less than the cost of renting (the pink line in the same panel), which has averaged 6.2 per cent. That is, on average, renters have been prepared to pay marginally more than owners. This result has surprised some home owners, who consider the non-financial benefits of ownership to be widely valued. However, it is qualitatively consistent with previous research (for example, Hill and Syed (2012), OECD (2005)), where a substantial risk premium is assumed. We take this average as an estimate of the non-financial benefits of renting. However, given the low quality of our early data and the extent of serial correlation, we would not place confidence in the precise point estimate or even its sign. However, the broader point, that the premium is small, is more robust to alternative expectational assumptions and variations in the sample.
Algebraically, the rental premium can be considered as an extra cost of ownership. If we add the premium to the left-hand side of Equation (3) and solve for π, we get the expected rate of capital appreciation that makes households indifferent between owning and renting:
Implicitly, we are assuming that the average non-financial benefits of renting relative to owning are constant over time, with otherwise unexplained price movements being attributed to expected capital gains. πe is shown as the dark line in Figure 2, calculated assuming a constant rental premium of 0.4 per cent of the value of housing. Under these assumptions, the latest (April 2014) estimate of expected appreciation rounds up to 2.9 per cent. This is higher than the break-even rate, because buyers need compensation for the risks and hassle of ownership. If potential home buyers expected house prices to rise faster than 2.9 per cent, then buying would be more attractive than renting, and buyers would bid up prices until the adjusted break-even rate matched their expectations.
Muellbauer (2012) argues that central banks should regularly survey home buyers regarding their expectations for capital appreciation. He argues that early detection of an imminent housing ‘bubble’ would facilitate macroeconomic stabilisation and prudential policies. He notes that simple measures – such as the change in house prices – which can be driven by changes in rents, interest rates and so on, are difficult to use for this purpose. Equation (7) provides another way of addressing this concern. Were our measure of expected capital appreciation to increasingly diverge from historic norms, that could be taken as a sign that optimism about capital gains was becoming self-reinforcing. Attractively for this purpose, Equation (7) can be updated in close to real time.
For example, Figure 2 shows that in 2003 home buyers were acting as though they expected real appreciation of almost 4 per cent a year. This was noticeably above the historical average of actual appreciation. At the time, many observers worried about the development of a housing bubble. Interestingly, buyers seem to have been similarly optimistic at other times, without overly worrying the authorities. We return to the 2003 boom in Section 6.
5.4 Discounted Cash Flows
Equation (3) assumes that each component of the user cost can be expressed as a constant rate. That greatly simplifies the computation and presentation of the results. In a more complicated but realistic model, components change over time and interact. These complications can be addressed by calculating expected cash flows over the period of ownership, discounting and then comparing present values.
To do this, we discount future cash flows at the real mortgage rate, on the assumption that households accommodate variations in cash flow by varying the pace at which their loan is paid off. We assume a house is owned for ten years, the median period of home ownership, after which a real capital gain is realised. We split transaction costs into buying costs, which occur at the beginning of an occupancy and selling costs, which occur at the end.
Perhaps the most important variation from the previous analysis is that we allow for growth in real rents over the period of ownership. The same forces that give rise to long-run real capital appreciation, specifically growing demand interacting with inelastic supply, would also lead to rising real rents. Indeed, Stapledon's (2007) historical time series for rents (which splice together the deflator for consumption expenditure on rent with the CPI measure) has increased 1.3 percentage points per year faster than the overall CPI, on average, since 1960. For simplicity, we assume a constant rental yield and solve for the common growth rate in both rents and house prices. As above, running costs are assumed to move in line with rents, and hence house prices.
These changes are small and their net effect is even smaller. The expected increase in real rents and the discounting of selling costs are partially offset by the discounting of capital gains. The net result is to make home ownership slightly more attractive, relative to renting. This can be seen in the break-even rates of appreciation shown in Figure 3. The light blue line reproduces the break-even appreciation rate from Figure 2, calculated using the static model described in Section 3, where the latest estimate, for April 2014, is 2.4 per cent. The orange line shows marginally lower estimates using discounted cash flows, for which the latest estimate is 2.3 per cent.
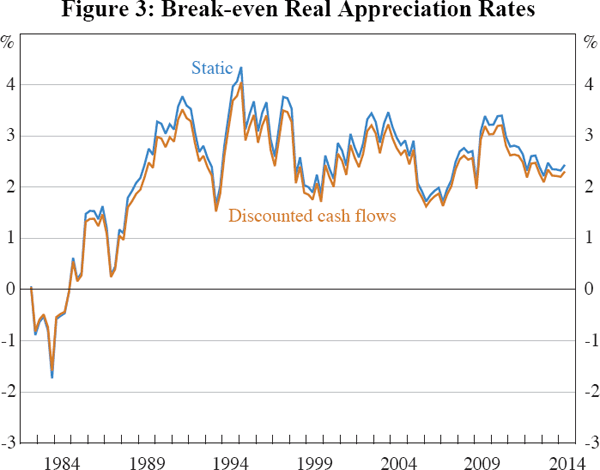
The insensitivity of our results to changing assumptions about growth in rents contrasts with the literature on stock market valuation, which finds substantial sensitivity to assumptions about earnings growth. The main reason is that studies of equity valuation typically assume that higher growth in earnings feeds back into greater appreciation whereas we do not.
Discounted cash flows provide a more comprehensive, and hence more accurate, measure of the relative costs of renting and owning than the static model. However, given that the results are similar, that distinction is unimportant for most purposes. Moreover, discounted cash flows are difficult to transparently decompose into interpretable components and so do not facilitate understanding or modification. Accordingly, we focus on explaining variations in the static user cost model (with some exceptions, such as Section 7.2).