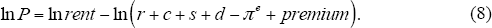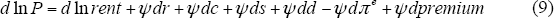RDP 2014-06: Is Housing Overvalued? 6. Decomposing Changes in House Prices

In Tables 1 and A1 we decompose the level of house prices into component parts. To decompose changes, we rearrange Equation (3), using Equation (7), so that house prices are explained by expected capital gains, the rental premium and other components of the user cost. In logs:

Totally differentiating:

where Ψ = −1/(r+c+s+d−π^e + premium) = −P/rent

The last step uses Equation (7). Equation (9) expresses the proportionate change in house prices as the sum of contributions from changes in rents and the user cost. Changes in components of the user cost are weighted by Ψ, the partial derivative of lnP with respect to the corresponding component, which equals minus the price-to-rent ratio.

Figure 4 shows the main elements of Equation (9). We take eight-quarter log differences, then multiply by 100/2 to express as approximate annualised percentage changes. We measure Ψ as the average of the values at the start and end of the eight-quarter period. We measure the growth of both house prices and rents in real terms. We do not show the zero contributions of depreciation and the rental premium, the tiny decomposition approximation error (mean zero, standard deviation 0.01 percentage points) or the small contribution from transaction costs (mean −0.12, standard deviation 0.15 percentage points). We show contributions from 1995, when data on 10-year fixed mortgages became available.

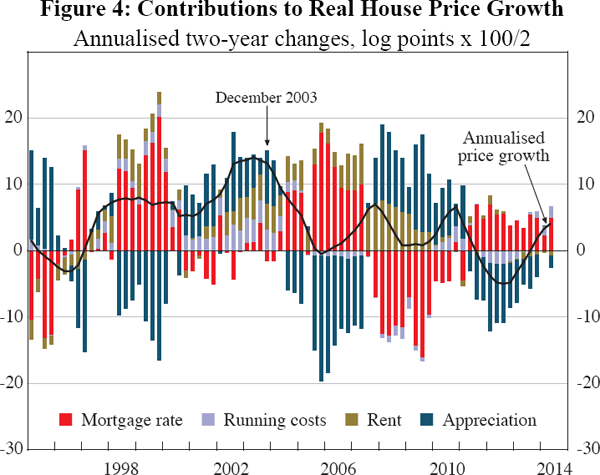
To illustrate, consider the two years to December 2003, when real house prices grew at a rapid annual rate of about 13 per cent. This increase is not attributable to mortgage rates which increased slightly. Rising real rents and a decline in the rate of running costs made moderate contributions (approximately 4 and 3 percentage points, respectively). As was often suggested at the time (see Bloxham, Kent and Robson (2010, Section 4.1)), most of the increase in prices can be attributed to higher expected capital appreciation. If expected real appreciation had remained at its December 2001 level of 3.2 per cent, instead of rising to 3.9 per cent, annual real house price growth would have been about 8 percentage points less.

More recently, real house prices have risen at an annual rate of 4 per cent in the two years to April 2014. This reflects a decline in mortgage rates (contributing 5 percentage points), which was partially offset by a decline in expected appreciation that subtracted 2 percentage points. The RP Data-Rismark measure of advertised rents rose slightly less than inflation over this period.