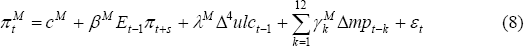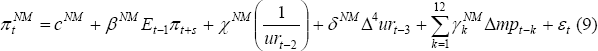RDP 2010-03: Modelling Inflation in Australia 4. Results
June 2010
- Download the Paper 498KB
4.1 Main Results
The estimates of each model are shown in Table 1 (fitted values are shown in Section 4.3). Overall, we find that the models fit the data quite well. They explain around 60 per cent of the variation in quarterly underlying inflation and have root mean squared errors (RMSE) that are generally less than 0.2 percentage points. In terms of the in-sample performance of each model, we find that the standard Phillips curve model fits best, followed by the mark-up model and then the two NKPC models. This is evident from assessing each model's AIC statistic, which is clearly lowest for the standard Phillips curve (indicating superior fit) and highest for the NKPC estimated with GMM.
| Standard PC | NKPC | OLS NKPC | Mark-up model | |
|---|---|---|---|---|
| Constant | −0.009** | 0.000 | 0.012*** | |
| Lagged inflation | 0.163 | 0.148 | ||
| Inflation expectations | 0.403*** | 0.837*** | 0.361*** | 0.309*** |
| Output gap | 0.020 | 0.166*** | 0.178*** | |
| Unemployment rate | 0.142*** | |||
| Δ unemployment rate | −0.003*** | |||
| Real unit labour costs | 0.039 | 0.125*** | ||
| Δ unit labour costs | 0.172* | |||
| Real import prices | 0.006 | 0.027** | ||
| Δ import prices | 0.079*** | −0.011** | −0.008 | 0.107*** |
| Adjusted R2 | 0.648 | 0.585 | 0.618 | |
| AIC | −9.91 | −9.23 | −9.75 | −9.81 |
| Log-likelihood | 403.5 | 368.7 | 396.9 | 401.4 |
| In-sample RMSE | 0.156 | 0.311 | 0.171 | 0.160 |
| Out-of-sample RMSE(a) | 0.188 | 0.299 | 0.254 | 0.231 |
| Durbin-Watson statistic | 2.14 | 2.04 | 2.00 | |
| Notes: ***, ** and * represent significance at the 1, 5 and 10 per cent
levels respectively. Where multiple lags are included, coefficients shown
are the sum of the lags. Coefficients on the constant, output gap, level
and change in unemployment rate, real unit labour costs and real import
prices are multiplied by 4 to represent annualised effects. (a) Six quarters ahead, using real-time internal RBA forecasts of dependent variables and calculated over the period since 2004. |
||||
The relatively poor performance of the NKPC estimated with GMM is also evident when we look at the individual coefficients. We do not find significant coefficients on any variable in the NKPC, except those relating to inflation and the change in import prices (though the latter is incorrectly signed). This finding is robust to different specifications of the driving variables, including estimating the model with the output gap and real unit labour costs separately, and deflating real unit labour costs by other price measures (including the gross national expenditure deflator). This result should perhaps not be surprising, however, given that other authors estimate insignificant coefficients on the driving variables in NKPCs based on Australian data (for example, Kuttner and Robinson 2010).
The results for the NKPC using OLS and direct measures of inflation expectations are more favourable. In particular, the coefficients on the driving variables are all now significant and sizeable (except for that on the change in import prices), and the overall fit of the model is markedly better than that estimated with GMM. However, the model does not fit the data as well as the standard Phillips curve and mark-up models.
In contrast to the GMM-based NKPC, the coefficients on both the standard Phillips curve and the mark-up model are all correctly signed and significant. For unemployment, the coefficients on the (inverse) unemployment rate and the change in the unemployment rate imply that (other things equal) a 1 percentage point decline in unemployment (from 5 per cent) would raise the (quarterly annualised) inflation rate by around ¾ of a percentage point for four quarters (beginning two quarters after the initial change in unemployment), before the speed limit effect fades and the inflation rate subsequently settles back around ½ of a percentage point above its initial rate. The estimated coefficients on inflation expectations in the two models are broadly similar (at 0.3–0.4), as are the elasticities of inflation with respect to import prices (at 0.1). The estimated elasticity of inflation with respect to unit labour costs in the mark-up model is around two-thirds larger than this. The coefficient on the output gap implies that a gap of 1 per cent has a direct effect of 0.2 percentage points on annualised inflation, though this does not reflect the total effect since the output gap term here captures only its effects on inflation through non-wage costs and the mark-up, and not its effects on inflation via wage costs and expectations.
The effects on inflation of movements in unit labour costs and import prices in these models are shown graphically in Figure 3. With regard to unit labour costs, the mark-up model implies that, other things equal, a 2½ per cent rise in unit labour costs (roughly corresponding to the standard deviation in annualised terms) would raise the (quarterly annualised) inflation rate by around 0.4 percentage points at its peak, which occurs around five to six quarters after the increase in unit labour costs. (Assuming no effect on inflation expectations or other variables, the effect on inflation is estimated to wash out after two years.) With regard to import prices, both the mark-up and standard Phillips curve models imply a very protracted pass-through to inflation. The mark-up model implies that the inflation rate would increase by a little more than ⅓ percentage point over each of the second and third years following a 10 per cent rise in import prices before washing out after almost four years.[11] Likewise, the standard Phillips curve model implies a three-year effect on inflation from higher import prices, with the estimated rise in the inflation rate being around ⅓ percentage point over the second year and slightly less in the third year. The protracted nature of these import-price effects may partly reflect inventory behaviour (firms typically clear older stock acquired at the original exchange rate before repricing). They may also reflect a deliberate response to volatility in the exchange rate (with some firms absorbing changes in import prices into their margins until they perceive that any exchange rate shock is permanent). However, it is not clear that such explanations can explain the sizeable effect on inflation that is ongoing three years after the shock. Nonetheless, this result is robust across a range of model specifications and time periods.
In order to assess the performance of these models, it is useful to compare their out-of-sample forecasts with those of some standard benchmarks. In particular, we compare these models to four alternatives: a constant annualised rate of 2½ per cent (the mid-point of the inflation target); the previous quarter's year-ended underlying inflation rate; a simple vector autoregression (VAR) model that uses the same variables that are included in the mark-up model;[12] and the factor-augmented VAR (FAVAR) model developed by Gerard and Nimark (2008). Real-time estimates of the regressors in the single-equation models are taken from internal RBA forecasts; as such, this exercise is not a ‘pure’ test of the forecasting ability of single-equation models, since forecasts of the independent variables are derived in a different manner from that used by the VAR or FAVAR models.
With this caveat in mind, this exercise suggests that the single-equation models generally perform better than these benchmarks. Table 2 presents the ratio of the root mean squared forecast error (RMSFE) of each model to that of a constant at various horizons, calculated between 2004 and 2009. All models perform somewhat better than the constant forecast, as reflected in ratios of less than one.[13] The standard Phillips curve model has the lowest RMSFE at all horizons, outperforming the benchmark models by at least 10 per cent, and considerably more at longer horizons. The performance of the mark-up model is very similar to each of the benchmarks at shorter horizons, but modestly superior at the eight-quarter-ahead horizon. The NKPC model estimated with OLS produces better forecasts over the long horizon than the benchmarks, but tends to produce inferior results over a shorter horizon.
| Single-equation models | Benchmark models | ||||||
|---|---|---|---|---|---|---|---|
| OLS NKPC | Standard PC | Mark-up model | Lagged inflation | Simple VAR | Factor-augmented VAR | ||
| 1 qtr ahead | 0.834 | 0.708 | 0.856 | 0.790 | 0.803 | 0.764 | |
| 4 qtrs ahead | 0.845 | 0.640 | 0.801 | 0.742 | 0.762 | 0.843 | |
| 8 qtrs ahead | 0.810 | 0.590 | 0.818 | 0.872 | 0.863 | 1.009 | |
| Notes: (a) For the period 2004–2009. RMSFE for 1-quarter-ahead horizon calculated from quarterly inflation rate, while 4- and 8-quarter-ahead RMSFEs are based on the year-ended inflation rate. | |||||||
4.2 Are There Benefits in Disaggregation?
An alternative approach to that used so far is to disaggregate inflation into some combination of the 90 items in the CPI, and estimate models for these disaggregated components. This allows the coefficients on input costs or expectations to vary across different types of products, although it may come at the cost of additional noise in the dependent variable. We split the sample of 90 items into two groups. The first includes items with prices predominantly determined by external factors (most importantly, the exchange rate). This largely consists of the manufactured items within the CPI, along with overseas travel; we loosely refer to this as the ‘manufactures’ group. The second group includes items with prices largely determined by domestic considerations, and we refer to this as the ‘nonmanufactures’ group.[14] Based on this classification, we calculate trimmed mean inflation for each series and use this as the dependent variable.
In each case we estimated both a standard Phillips curve and a mark-up model of inflation. We present the models which fit best, with the mark-up specification clearly superior in the case of manufactured items and the standard Phillips curve marginally superior for non-manufactured items. The model for manufactures inflation is:
where: the superscript M refers to the group of manufactured items; input costs and inflation expectations are economy-wide measures (due to data limitations); and the coefficients on import prices are constrained to follow a quadratic PDL specification.[15] For inflation of the non-manufactures group (NM), the model is:
where the coefficients on import prices are also constrained using a quadratic PDL specification.
The results of this are shown in Table 3. Not surprisingly, import prices are an important explanator of manufactures prices, while domestic determinants (inflation expectations and labour market conditions) are more important for non-manufactures. The fitted values can be aggregated based on the relative share of manufactured and non-manufactured items in the CPI. This combination of the disaggregated models produces broadly comparable results to those from the aggregated model, in terms of in-sample fit and out-of-sample fit. In addition, the implied sensitivity of overall inflation to movements in input costs is also similar, especially for import prices (at just over 0.1). These results suggest that the gains from the disaggregate approach come primarily from its usefulness in illustrating some underlying influences, with its econometric performance providing no strong reason to prefer it.
| Manufactured items | Non-manufactured items | Aggregate results(a) | |
|---|---|---|---|
| Constant | −0.011** | −0.003 | |
| Inflation expectations | 0.358*** | 0.425*** | |
| Unemployment rate (inverse) | 0.140*** | ||
| Δ unemployment rate | −0.003*** | ||
| Δ unit labour costs | 0.117 | ||
| Δ import prices | 0.309*** | 0.032 | |
| Adjusted R2 | 0.395 | 0.684 | |
| In-sample RMSE | 0.380 | 0.152 | 0.159 |
| Out-of-sample RMSE(b) | 0.477 | 0.209 | 0.246 |
| Durbin-Watson statistic | 2.42 | 1.75 | |
| Notes: ***, ** and * represent significance at the 1, 5 and 10 per cent
levels respectively. Where multiple lags included, coefficients shown are
sum of the lags. Coefficients on constant and the level and change in the
unemployment rate are multiplied by 4 to represent annualised effects. (a) RMSE is calculated as a weighted average of manufactures and non-manufactures regressions. (b) Six quarters ahead, using real-time internal RBA forecasts of dependent variables and calculated over the period since 2004. |
|||
4.3 Historical Fit of the Models
Figure 4 shows the year-ended fitted values of the NKPC (estimated with both GMM and OLS), the standard Phillips curve, the mark-up model and the weighted average of the models for manufactures and non-manufactures (referred to hereafter as the ‘disaggregate’ model). To account for the lead of inflation in the GMM-based NKPC, the fitted values from that model are estimated using the closed form implied by the model, as in Galí and Gertler (1999) and Sbordone (2002).[16]
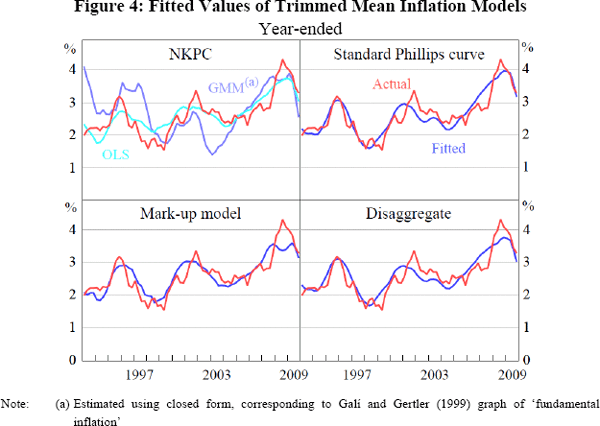
This evidence reinforces that obtained from the regression results that the standard Phillips curve and mark-up models provide a better description of inflation than does the NKPC. The standard Phillips curve and mark-up models track the cycle in inflation more closely, and better capture the pick-up in inflation in 1995, 2001 and 2007–2008. Likewise, the disaggregate model provides a relatively good explanation of aggregate inflation over much of the sample, with the fitted values from it resembling those from the standard Phillips curve model at most points in the sample. The relatively good performance of the disaggregate model reflects the performance of both its components (Figure 5). The manufacture and non-manufactures models both fit the data well, although the non-manufactures model suggests an earlier and smoother pick-up in domestic inflation over 2005–2008 than actually occurred, and the manufactures model does not explain the full extent of imported inflation that occurred in 2001.
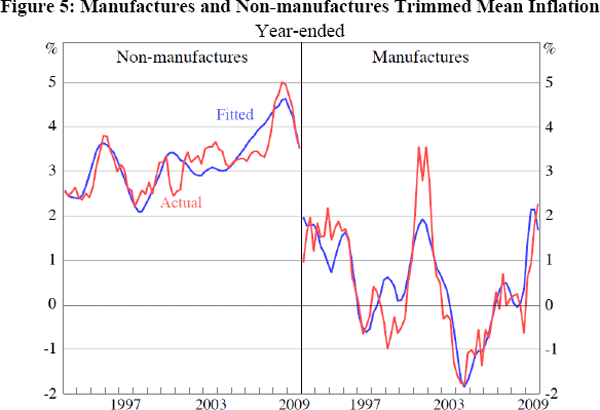
In contrast, the GMM-based NKPC model produces large and persistent errors. This may in part reflect the simplicity of our forecasting models for the driving variables, which do not capture much of the variation in these series, although it likely also reflects the significant and persistent fluctuations in real import prices over the sample, which have a longer-lasting effect on the NKPC than other models. Using OLS to estimate the NKPC partially resolves these issues, with the model having a closer fit. Nonetheless, the OLS version of the NKPC still displays much larger errors than the other models.
All models correctly suggest a substantial acceleration in inflation between 2005 and 2008. Estimates from the standard Phillips curve are closest to the true outcome, at around 4 per cent by late 2008, while those from the other models are moderately lower than actually occurred, at around 3½–3¾ per cent. This estimated pick-up is consistent with the trend decline in the unemployment rate over that time and associated strength in unit labour costs growth, along with a sizeable output gap and fading disinflation from import prices. All models also explain the disinflation that occurred through 2009.
Footnotes
Dwyer and Leong (2001) suggest that just over half of any shock to the exchange rate is estimated to flow into across-the-docks import prices within the quarter, with the remainder flowing through in the following quarter. [11]
To conserve degrees of freedom, only one lag of each endogenous variable (trimmed mean inflation, inflation expectations, the output gap and quarterly growth in unit labour costs) is included, but the model is augmented with various lags of year-ended unit labour costs and import price growth to capture the same lag length as in the mark-up model. [12]
The exception is the GMM-estimated NKPC (not shown), whose forecasts are found to be no better at all horizons. [13]
The main manufactured items excluded from the manufactures group are alcohol & tobacco, pharmaceuticals, and books & newspapers (whose prices appear to be largely determined domestically). Automotive fuel was excluded from both groups, as its weight dwarfs all other items in the manufactures classification where it would naturally fit. (This introduces an inconsistency with the earlier results, but it is not a material one.) Deposit & loan facilities were also excluded from the estimation, consistent with our approach at the aggregate level. The resulting grouping has some similarity to the tradable/non-tradable split published by the ABS, with the main difference being that a range of food items that are tradable are included in our non-manufactures series since their prices appear to be largely influenced by domestic factors. [14]
The use of the year-ended change specification for unit labour costs is equivalent to the inclusion of four quarterly lags that are constrained to be equal. [15]
More specifically, we first estimate two recursive VAR models and a recursive autoregressive model to forecast unit labour costs, import prices and the output gap respectively, in a similar manner to Sbordone (2002). The VAR for unit labour costs (import prices) includes two lags each of the growth rate of nominal unit labour costs (import prices) and the level of the mark-up of consumer prices on unit labour cost (mark-up of consumer prices on import prices). Each model is estimated from 1982:1 to period t, and is used to forecast the driving variables 12 quarters ahead starting in t+1. The discounted sum of these forecasts is then included in the closed form solution, as per Galí and Gertler (1999), with equations for the characteristic roots found in Galí et al (2005). [16]