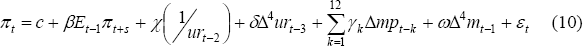RDP 2010-03: Modelling Inflation in Australia 5. Investigating the Role of Other Variables or Restrictions

The literature on inflation models contains a much larger set of candidate variables than those used above. Furthermore, there is considerable debate about how to best proxy inflation expectations, and many other papers impose the restriction that there is no long-run trade-off between inflation and the unemployment rate or output gap, which we have not done. Given this, it is useful to check what effect such variations would have on our results. We pursue four issues: the effect of imposing a vertical long-run Phillips curve restriction on our models; whether there are better proxies for inflation expectations; what influence commodity prices have on inflation; and the possible role of money growth.^[17] In each case, we adapt the standard Phillips curve, the OLS NKPC and the mark-up model with these restrictions or additional variables. The details of each regression can be found in Appendix B.

5.1 A Vertical Long-run Phillips Curve Restriction

The concept of a vertical long-run Phillips curve – that is, that there is no trade-off in the long run between unemployment and inflation – is a cornerstone of most inflation models and has a long history in the literature (beginning with the rational expectations revolution in the 1970s). Indeed, this idea underlies the pursuit of price stability by central banks in most industrial countries.

However, neither our standard Phillips curve, the mark-up model nor the OLS NKPC incorporate this standard feature. This reflects the fact that the sum of the coefficients on the right-hand-side nominal variables (inflation expectations, and growth in unit labour costs and import prices) in each of these models is significantly less than unity. This result survives when we simplify the models to represent inflation as being driven solely by inflation expectations and the output gap or unemployment rate; in that case, the coefficient on inflation expectations is significantly different from 1 for samples beginning in or after 1987. The rejection of this restriction is, however, not unique to our work; for example, both Anderson and Wascher (2000) and Williams (2006) have found such a result using US data.

There are several possible explanations for this result. One relates to econometric issues, including from the relatively small sample used in estimation, or the possibility of a bias to our coefficients from measurement errors in our regressors. For example, our measure of expectations of inflation over the next 10 years is likely to be imprecisely measured (as are other measures of expectations) and only imperfectly correlated with the expectation that influences price-setting (which is likely to be for a one- or two-year horizon). However, it is hard to assess how important these effects are, and the long-run restriction is also obtained if we use a measure of shorter-term (one- or two-year) inflation expectations derived from the term structure of bond yields. Another possible explanation is suggested by Akerlof, Dickens and Perry (2000), namely that it may be ‘near rational’ for agents to devote limited attention to inflation when it is at low levels, resulting in the long-run Phillips curve appearing to be non-vertical within a range of low inflation outcomes.

Regardless of the reasons, it is clear that the models estimated above are not ‘structural’, in that they would not be robust to examining episodes of high inflation. One response to such concerns would be to impose the property of long-run neutrality on our models. This can be done by respecifying the mark-up model with the coefficients on the nominal terms constrained to sum to unity, which is equivalent to deflating all nominal variables (including the dependent variable) by inflation expectations. However, this results in a deterioration of fit, with the adjusted R-squared falling from 0.62 to 0.45, and the introduction of mild serial correlation. This serial correlation arises because the coefficients on the input cost terms increases significantly, from 0.17 to 0.48 for unit labour costs and 0.11 to 0.27 for import prices, causing the model to consistently under-predict inflation following currency appreciations and over-predict inflation following currency depreciations. Nonetheless, this model might be more robust in the event that inflation expectations become dislodged and so may be a useful addition to any suite of models.

5.2 Different Measures of Inflation Expectations

This discussion highlights some of the potential difficulties with the inflation expectations measure used in our models. While it is commonly accepted that inflation expectations are a critical influence on inflation outcomes, there is no consensus on how to model such expectations appropriately. The traditional approach has been to proxy inflation expectations with lagged inflation (as in Brayton et al 1999, for example), while the New-Keynesian approach of instrumenting for expected inflation using lags of inflation (as well as the output gap and unit labour costs) is essentially equivalent. Both of these, however, have well-understood limitations. An alternative approach is to use survey or financial market measures of inflation expectations (for example, Gruen et al 1999 and Henzel and Wollmershäuser 2008). We test the sensitivity of our results to these different approaches.

The results imply that, for both the mark-up and standard Phillips curve models of inflation, the bond market measure provides the best in-sample fit. The results of Section 4 have shown that using instruments for inflation expectations is inferior to including the bond market measures of inflation expectations. The bond market measure also provides a better fit than lagged year-ended inflation; the explanatory power falls when we include lagged inflation instead (Table B1) and its coefficient is insignificant when included alongside the bond market measure (result not shown). The bond market measure also provides a superior fit to either the Melbourne Institute's survey measure of consumer expectations (Table B1)^[18] or measures of shorter-term inflation expectations implied by financial markets (result not shown). All of these results are invariant to whether the sample begins in 1990 or 1993.

5.3 The Influence of Oil Prices

Many papers modelling inflation include a measure of oil or other commodity prices in their equations (see, for example, Gordon 2005). In most instances, such regressions use headline rather than underlying (or ‘core’) inflation, providing a strong rationale for the inclusion of oil prices in the equation.^[19]

To investigate whether there is a role for oil prices in explaining underlying inflation in Australia, we augment our aggregate regressions with lagged growth in (Australian dollar) crude oil prices (or the level of real oil prices in the NKPC). We test for up to six years of lags, although to preserve degrees of freedom we constrain the quarterly responses to be equal within each year.

The results from this exercise present mixed evidence on the role of oil prices (Table B1). The mark-up model provides support for a statistically significant effect of movements in oil prices; also, the overall explanatory power rises modestly compared with the baseline and a likelihood ratio test is able to reject the hypothesis that oil prices have no effect on underlying inflation at the 10 per cent level.^[20] However, there are a number of concerns with these results, including the very long lag between oil price changes and underlying inflation estimated by the model (three to four years), sensitivity to the lag structure, and the insignificance of oil prices in the Phillips curve models. Overall, these results provide only limited support for the presence of an effect on underlying inflation from oil price growth, independent of its effect via inflation expectations or the output gap.^[21]

5.4 Monetary Models of Inflation

There is a long tradition of modelling inflation as a function of growth in the money supply, based on Milton Friedman and Anna Schwartz's observation that ‘inflation is always and everywhere a monetary phenomenon’. While this is no longer considered to imply that central banks should target growth in the money supply, there is still some debate about whether money should be considered when modelling inflation. For example, the European Central Bank's ‘two-pillar’ monetary policy framework might suggest such an approach, relating short- to medium-term inflation to real factors (such as output and unemployment gaps) and medium- to long-term inflation to growth in the money supply. However, many economists of the New Keynesian tradition have argued to the contrary, suggesting that money is ‘obsolete’ in a properly specified model that includes a monetary policy rule (see, for example, Woodford 2007). Given these differences, it is of interest to assess whether money growth has any explanatory power for Australian inflation. This could arise for a variety of reasons unrelated to whether it is appropriate to include money in a structural model of inflation; for example, trend money growth could provide a better (or complementary) proxy for inflation expectations than the bond market measure, or might control for measurement error in unit labour costs.

We use an approach adopted by Gerlach (2004), who augments a NKPC model with a measure of trend money growth. Gerlach motivates this specification on the basis that the NKPC captures short- to medium-term movements in inflation, while trend money growth will capture the medium- to long-run movements in inflation. We implement a version of this approach, but capture the short- to medium-term dynamics of inflation with the standard Phillips curve model. Specifically, we supplement Equation (5) with a term for money growth and estimate the following specification:

where: the notation is as in Equation (1); the coefficients on import prices follow a PDL specification; and Δ⁴m represents trend excess money growth, defined as the band-pass filtered trend in the stock of money divided by nominal GDP. We test two different measures of money (M3 and broad money) and also test for a role for credit growth. The band-pass filter removes the last three years of data, leaving us with a sample that ends in the March quarter 2007.

The results from this regression provide modest evidence that growth in money or credit may be empirically relevant for future inflation over the period since 1990, once other determinants have been included: trend excess M3 growth is significant at the 10 per cent level (Table B1). However, the inclusion of this variable causes the coefficient on the level of the unemployment rate to become insignificant. Moreover, neither excess broad money – which should be more relevant on a priori grounds – nor credit growth are significant at anywhere near a conventional level of significance. Given the lack of uniformity in these results, and the insignificance of the level of the unemployment rate when M3 is included, we conclude that the inclusion of money in our inflation models does not impart significant benefit.

Footnotes

We also looked at a possible role for the world output gap, but found no support for this (results available from the authors on request). [17]

One difficulty with using the Melbourne Institute's measure is that it contains a structural break in 1993, prior to which negative responses were excluded from the calculation. This results in the current series being a full percentage point above the old series in 1993. To ensure consistency back to 1990, we assume that this gap remains constant from 1990 to 1993, and adjust down the old measure accordingly. [18]

The international evidence on whether to include oil prices in a regression for underlying inflation is limited. One comprehensive assessment of this question is provided by Hooker (2002), who finds that while oil prices were a significant explanator of core inflation in the United States prior to 1980, they play an insignificant role thereafter. In contrast, Cheung (2009) finds that persistent movements in oil prices have been a useful predictor of core inflation since 1990 across a range of countries. While Hooker argues that his results stem from a change in policy by the Federal Reserve since 1980 to not accommodate oil price shocks, the difference between his results and those of Cheung suggests that it might instead reflect the relative stability of oil prices between 1980 and 2000. In other words, the sharp rise in oil prices between 2003 and mid 2008 could explain Cheung's finding of significant second-round effects. [19]

The elasticity of inflation with respect to movements in crude oil prices in the mark-up model is estimated to be 0.018 (not including any second-round effects, for example on inflation expectations) which implies that the more than doubling of oil prices in the four years to late 2008 contributed almost ½ a percentage point to annual inflation. Rolling regression estimates suggest that this relationship is only identifiable during periods of large changes in oil prices, since the coefficients are insignificant in samples that exclude the past few years. [20]

We also tested for the inflationary effect of commodity prices more generally, using the CRB commodity price index (in Australian dollar terms). We do not find a significant coefficient on year-ended growth in commodity prices over most sample periods. [21]