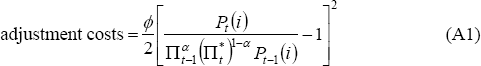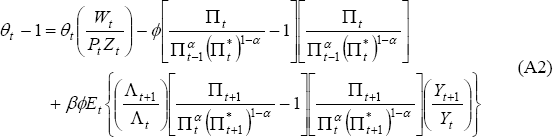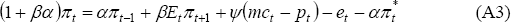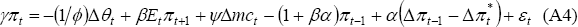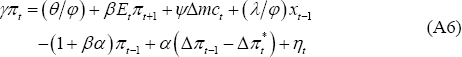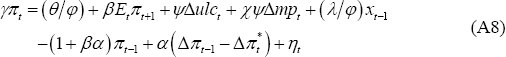RDP 2010-03: Modelling Inflation in Australia Appendix A: Derivation of the Mark-up Model of Inflation

The derivation of the expectations-augmented mark-up model of inflation used in this paper is based on Ireland's (2007) model. This model is a relatively standard New-Keynesian micro-founded model, with a representative household that maximises expected utility (flowing from consumption and holdings of real money balances) and a representative firm that maximises expected profits. The firm is found to only adjust its prices periodically, given the assumption that it faces quadratic adjustment costs to alter prices (in the spirit of Rotemberg 1982). These costs are defined as:

where P(i) is the price charged by (the representative) firm i; Π is the aggregate inflation rate and Π^* is the central bank's inflation target; α is a parameter that governs the degree to which prices are set with reference to an inflation target (α = 0) or to past inflation (α = 1); and ϕ ≥ 0 governs the magnitude of price-adjustment costs.

As shown in Ireland (2007, Equation (A6)), the optimal price adjustment implies:

where: θ is the (time-varying) price elasticity of substitution for intermediate goods; W is the nominal wage; Z is the technology shock; β is the household discount factor; Λ is the marginal utility of wealth; and Y denotes aggregate output.

Ireland shows that this equation implies that inflation evolves as follows:

where: (mc − p) represents real marginal costs; e_t represents a mark-up shock (θ_t/ϕ); and all variables are expressed as percentage deviations from steady-state level.

The model used in this paper deviates from Ireland's approach in three ways. First, we express the inflation process in a different way, in order to show that inflation can be represented as a function of growth in nominal marginal costs, rather than the level of real marginal costs. Second, we allow mark-ups to be a function of aggregate resource utilisation. Third, we define marginal costs to include both labour and import prices. Each of these changes is discussed below.

To express inflation as a function of the change in nominal marginal costs, our point of departure from Ireland's model is to take the first-order difference equation of (A3). This results in the following expression:

where: γ = (1 + β + βα + ψ); and ε_t = β(π_t − E_t−1π_t) is an expectational error term that, by the assumption of rational expectations, is a white noise process.

Our second modification to Ireland's model is to assume that −θ_t – the time-varying elasticity of substitution for intermediate goods – is related to aggregate resource utilisation in the economy.^[24] This assumption can be motivated by either of two explanations. The first is that marginal costs are not perfectly equated across capital and labour, such that −θ_t captures the effect of procyclical capital costs. The second is that firms' desired mark-ups over marginal cost (which are θ_t/(θ_t − 1) according to Equation (A2)) may be procyclical if consumers' demand for goods becomes less price elastic as overall capacity utilisation rises.^[25] The assumption that the output gap and mark-ups are positively correlated (that is, that mark-ups are procyclical) is non-standard in US research (see, for example, Rotemberg and Woodford 1999, where it is comprehensively argued that mark-ups are countercyclical), but the evidence is less supportive of countercyclical mark-ups in other countries. For example, Macallan, Millard and Parker (2008) find that the mark-up is procyclical for the United Kingdom, de Brouwer and Ericson (1995) and Stone et al (2005) both find that the output gap enters significantly into a mark-up model of inflation in Australia, and the profit share in Australia appears to be procyclical, which cannot occur if mark-ups are countercyclical (in which case profits can rise, but not by more than output).

This modification is achieved by assuming that θ_t can be represented by the following process:

which implies that θ_t is decreasing in last period's output gap, x_t−1, so that the mark-up – θ_t/(θ_t − 1) – is increasing in last period's output gap. Substituting (A5) into (A4) implies the following inflation process:

where η_t = ε_t + (1/φ)ν_t

The third change is to specify marginal costs as a function of both labour and import costs, as in Bentolila and Saint-Paul (2003). This specification is based on the assumption that firms use a material input to produce gross output, and that the proportion of material input required per unit of gross output increases as output expands. Under these assumptions, Bentolila and Saint-Paul show that marginal costs are a function of both unit labour costs and import prices, as follows:

Given this, we arrive at our final specification for the inflation process:

Footnotes

By assuming that the elasticity of substitution for each good is related to aggregate resource utilisation, rather than the firm's own utilisation, we do not influence the standard derivation of the optimal price adjustment. [24]

This specification does not imply that the output gap only influences inflation via mark-ups. Rather, it presumes that the output gap affects inflation both as a partial determinant of marginal costs and as a determinant of mark-ups. [25]