RDP 2009-03: Competition Between Payment Systems: Results 3. The Effects of Competition on Platform Pricing
April 2009
We turn now to the results obtainable from our ECR model and from its restricted version, the CR model. These results relate both to the overall level of fees charged by competing platforms and, more strikingly, platforms' allocation of these fees across the two sides of the market.
In the case of the CR model, the scenario results we report are computed using the analytical solutions to this model which we have been able to derive – see Gardner and Stone (2009b) for details. For our ECR model they are instead obtained via numerical simulation, since the greater complexity of this model renders it impractical to solve analytically. We report results to three decimal places but, for those obtained numerically, the solution grid used in solving each platform's fees means that these may not be precisely accurate in the third decimal place. Hence, in what follows we regard solutions in which all model variables differ only by ±0.001 as equivalent.
For the scenarios considered below, the two platforms in the CR or ECR models are assumed to be identical in: the maximum benefits they provide to consumers and merchants (τi = τj = τ, μi = μj = μ); and their costs (ci = cj = c, gi = gj = g). We also focus throughout on symmetric model solutions, in which both platforms' fees to merchants are the same, as are their fees to consumers. Chakravorti and Roson (2006) investigated five such scenarios, and we concentrate on the three of these where τ = μ = 1. These scenarios correspond to situations where platforms: face no costs (Scenario 1); face no costs in signing up consumers, but do face per-transaction costs (Scenario 2); and face per-subscriber costs but no per-transaction costs (Scenario 3). Table 1 presents results for these three scenarios, for both the CR and ECR models, in the duopoly case.[10] Note that Table 1 also contains results for a third model, denoted the PTP (or Per-transaction Pricing) model, which is developed later; these results are discussed in Section 4.3.
| Variable | Scenario 1 | Scenario 2 | Scenario 3 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| g = c = 0 | g = 0, c = 0.5 | g = 0.2, c = 0 | |||||||||
| CR | ECR | PTP | CR | ECR | PTP | CR | ECR | PTP | |||
| Platform fees | |||||||||||
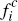 |
0.180 | 0.086 | – | 0.247 | 0.148 | – | 0.360 | 0.360 | – | ||
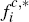 |
0.236 | 0.155 | 0.314 | 0.449 | 0.336 | 0.494 | 0.449 | 0.450 | 0.536 | ||
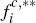 |
– | 0.242 | – | – | 0.540 | – | – | 2.250 | – | ||
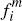 |
0.236 | 0.305 | 0.262 | 0.449 | 0.532 | 0.478 | 0.200 | 0.200 | 0.172 | ||
| Consumer market fractions | |||||||||||
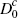 |
0.056 | 0.024 | 0.099 | 0.202 | 0.113 | 0.244 | 0.202 | 0.203 | 0.287 | ||
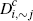 |
0.472 | 0.201 | 0.215 | 0.399 | 0.338 | 0.250 | 0.399 | 0.399 | 0.249 | ||
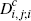 |
0.000 | 0.287 | 0.235 | 0.000 | 0.106 | 0.128 | 0.000 | 0.000 | 0.108 | ||
| Merchant market fractions | |||||||||||
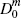 |
0.056 | 0.093 | 0.069 | 0.202 | 0.283 | 0.228 | 0.040 | 0.040 | 0.030 | ||
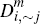 |
0.180 | 0.354 | 0.336 | 0.247 | 0.275 | 0.296 | 0.160 | 0.160 | 0.246 | ||
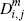 |
0.584 | 0.199 | 0.260 | 0.303 | 0.167 | 0.180 | 0.641 | 0.640 | 0.478 | ||
| Other | |||||||||||
| Πi | 0.170 | 0.180 | 0.200 | 0.088 | 0.089 | 0.103 | 0.127 | 0.128 | 0.109 | ||
| Voli | 0.361 | 0.372 | 0.347 | 0.220 | 0.225 | 0.218 | 0.319 | 0.319 | 0.285 | ||
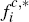 + +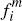 |
0.472 | 0.460 | 0.576 | 0.899 | 0.868 | 0.972 | 0.649 | 0.650 | 0.708 | ||
| AvgPPTi | 0.472 | 0.484 | 0.576 | 0.899 | 0.894 | 0.972 | 0.649 | 0.650 | 0.708 | ||
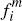 / AvgPPTi / AvgPPTi |
0.500 | 0.630 | 0.455 | 0.500 | 0.595 | 0.492 | 0.307 | 0.307 | 0.243 | ||
| Notes: CR denotes the Chakravorti and Roson model; ECR denotes the Extended Chakravorti and Roson model; and PTP denotes the Per-transaction Pricing model (introduced in Section 4 below). For simplicity, results are shown in units such that C and M both equal 1, and the common value of τ and μ is also 1. Voli denotes the volume of transactions that take place on platform i, while AvgPPTi denotes the average price per transaction on platform i. Notation for all other variables is as in Gardner and Stone (2009a) – see also Appendix A. | |||||||||||
From Table 1 we see that the ECR model outcome for Scenario 3 is the same as that for the CR model. This reflects the fact that, even though multi-homing by consumers is permitted in our ECR model, for this scenario the two platforms' Nash equilibrium price settings turn out to make it unattractive for any consumers to hold both platforms' cards.
For Scenarios 1 and 2, however, the ECR model outcomes are different from those for the CR model. In these cases, the fees which symmetric competing platforms will adopt in Nash equilibrium, when consumers are allowed to multi-home, turn out to be consistent with some consumers opting to do so – placing us firmly in the non-CR world. We now analyse the results in Table 1 for these two scenarios in greater detail.
3.1 Duopoly Results for the ECR Model
For Scenarios 1 and 2 in the ECR model, some consumers do find it optimal to hold
the cards of both platforms 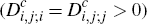 .
This, in turn, induces some merchants to opt to steer cardholders, which accounts
for the higher fraction of single-homing merchants in the ECR model in each
of these scenarios (compare
.
This, in turn, induces some merchants to opt to steer cardholders, which accounts
for the higher fraction of single-homing merchants in the ECR model in each
of these scenarios (compare 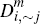 values).
values).
It is interesting next to compare platforms' total price levels in the two models,
for Scenarios 1 and 2. Before doing so, however, it should be noted that the
price level is not as well-defined a concept in our ECR model as it is in
the CR model (or, more generally, in a world of purely per-transaction pricing).
When platforms levy only per-transaction fees their price level may be defined
simply as 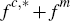 ,
which represents the total price paid by consumers and merchants for any given
transaction. By contrast, when consumers face flat rather than per-transaction
charges and may multi-home, as in our ECR model, different consumers may face
different effective per-transaction charges for using (say) platform i
(depending on their preferences for using card i or card j).
,
which represents the total price paid by consumers and merchants for any given
transaction. By contrast, when consumers face flat rather than per-transaction
charges and may multi-home, as in our ECR model, different consumers may face
different effective per-transaction charges for using (say) platform i
(depending on their preferences for using card i or card j).
Specifically, consumers who will use card i whenever possible face an effective per-transaction fee for doing
so of 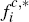 .
However, those who subscribe to both platforms but prefer to use card j
face a higher effective per-transaction fee for card i transactions
of
.
However, those who subscribe to both platforms but prefer to use card j
face a higher effective per-transaction fee for card i transactions
of 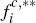 – since they pay the same flat subscription fee but will undertake fewer card
i transactions. Hence, in our ECR model, the quantity
– since they pay the same flat subscription fee but will undertake fewer card
i transactions. Hence, in our ECR model, the quantity 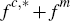 no longer reflects
the effective total price paid universally by consumers and merchants
for any given transaction.
no longer reflects
the effective total price paid universally by consumers and merchants
for any given transaction.
In Table 1 we adopt two approaches to handling this complication. The first is to
continue to report 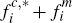 for our ECR model, since this remains the effective total price paid for the bulk
of transactions. This reflects that, for symmetric platform fee settings,
consumers who prefer to use card i wherever possible (those in sets
for our ECR model, since this remains the effective total price paid for the bulk
of transactions. This reflects that, for symmetric platform fee settings,
consumers who prefer to use card i wherever possible (those in sets
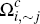 and
and 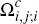 )
outnumber, sometimes by a significant margin, those who hold both cards but
prefer to use card j
(those in set
)
outnumber, sometimes by a significant margin, those who hold both cards but
prefer to use card j
(those in set 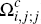 ). The second is to report also the average
price per transaction, AvgPPTi, obtained by dividing platforms'
total revenue from consumers and merchants by their total number of transactions.
). The second is to report also the average
price per transaction, AvgPPTi, obtained by dividing platforms'
total revenue from consumers and merchants by their total number of transactions.
On either measure, the most notable feature of the price level results for Scenarios 1 and 2 is how little difference there is between the CR and ECR models in each case. While AvgPPTi is marginally higher for the ECR than for the CR model in Scenario 1 (0.484 versus 0.472), it is marginally lower in Scenario 2 (0.894 versus 0.899); and in neither case is the difference noteworthy. Hence, for these scenarios at least, permitting consumer multi-homing does not seem to significantly affect competing platforms' equilibrium price level settings.[11]
By contrast, the effect of allowing endogenous consumer multi-homing on platforms' allocation of their fees between the two sides of the market is striking. For Scenarios 1 and 2, these allocations are evenly balanced for the CR model, with fc,* equal to fm. Once consumer multi-homing is permitted in the ECR model, however, they become strongly tilted in favour of consumers over merchants – by a factor of around 2 for Scenario 1, and around 1.6 for Scenario 2.[12]
While the strength of this shift is worthy of comment in its own right, more noteworthy still is its direction! The only difference between the CR and ECR models is that consumers in the CR model are prohibited from multi-homing – which is equivalent to their being imbued with an overwhelming propensity to single-home. A common finding in the literature to date on competition between payment systems has been that an increase in the tendency to single-home on one side of the market will lead platforms to price more attractively to that side. One might therefore have expected competing platforms, in Scenarios 1 and 2, to tilt their prices more heavily in favour of consumers in the CR model than in the ECR model. This, however, is the exact opposite of what we find. The results in Table 1 therefore immediately raise the question: why do platforms in our ECR model framework behave in a way contrary to that which might have been expected, based on the literature to date?
3.2 The Incentives Driving Platforms' Price Allocation Decisions
To address this question, it is useful to begin by reviewing the features of those models which have been used thus far to find a nexus between increases in a side's propensity to single-home and more attractive pricing by platforms to that side. Identifying features common to these models, but not to our ECR framework, should help to isolate the factors driving our contrary finding.
When we conduct such a review – albeit only a partial one – one thing which stands out is that those models which have yielded such a nexus all effectively involve purely per-transaction pricing by platforms to both sides of the market (see, for example, Armstrong 2006 and Rochet and Tirole 2003). Hence, a natural candidate for a driver of our contrary finding is the presence of flat rather than per-transaction pricing to consumers in our ECR model.
One way to test this hypothesis explicitly is to: construct a third model of payments system competition, equivalent to our ECR model except with per-transaction rather than flat pricing to consumers; and then compare numerical simulations of this model with those for the CR and ECR models, for the same three scenarios considered in Table 1. We take up such an approach in Section 4.
First, however, it is instructive to ask how, intuitively, we would expect flat rather than per-transaction pricing to consumers to affect platforms' price allocation incentives, in the face of a change in consumers' propensity to single-home. Clearly, in a world of purely per-transaction pricing, the goal of profit-maximising platforms is to maximise their volume of transactions, for any given total price level. As one side becomes more inclined to single-home, research to date suggests that this entails courting that side more aggressively, since ‘platforms have monopoly power over providing access to their single-homing customers for the multi-homing side ... [which] naturally leads to high prices being charged to the multi-homing side’ (Armstrong 2006, p 669).
In a world of flat fees to consumers, however, it may be profitable for platforms to pursue a class of consumers who will actually bring relatively few transactions to the platform. For platform i (say) these are the consumers who would prefer to use card j over card i if possible, but who might still judge it worthwhile to subscribe to platform i in addition to platform j, provided the subscription fee is not too high. Such consumers will now pay the same revenue to platform i as its other subscribers (those who subscribe to platform i only and those who subscribe to both platforms but prefer to use card i over card j), despite bringing fewer transactions – and clearly the prospects of attracting such subscribers will rise the less inclined consumers are to single-home.[13]
Another way to put the same point is to note that, when platforms charge only per-transaction
fees, all consumers will pay the same amount per transaction to (say) platform
i, namely 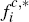 . This would make consumers that hold both
cards but prefer to use card j of limited value to platform i,
given the relatively small number of transactions these consumers will make
on the platform. By contrast, when platforms charge flat fees to consumers,
those same subscribers pay a higher effective per-transaction fee,
. This would make consumers that hold both
cards but prefer to use card j of limited value to platform i,
given the relatively small number of transactions these consumers will make
on the platform. By contrast, when platforms charge flat fees to consumers,
those same subscribers pay a higher effective per-transaction fee, 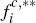 , than subscribers
who use card i whenever possible, giving platform i an incentive
not to focus solely on maximising transaction volume, for a given level of
, than subscribers
who use card i whenever possible, giving platform i an incentive
not to focus solely on maximising transaction volume, for a given level of
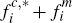 .
.
These observations suggest a way in which the use of flat rather than per-transaction fees to consumers might create a countervailing incentive for platforms to court consumers more aggressively, not as their tendency to single-home rises, but rather as it falls.
Footnotes
The corresponding monopoly results are reported in Table 2 in Section 5. We omit them here because they turn out to be identical, for each scenario, across both the CR and ECR models. [10]
It also leaves intact Chakravorti and Roson's (2006) observation that this price level will be lower under duopoly than monopoly – compare the ECR model results in Table 1 with those in Table 2 in Section 5. [11]
Of course, since some consumers pay a higher effective per-transaction price of fc,** for certain card transactions in the ECR model, these figures somewhat overstate the extent of the shift in favour of consumers. Nevertheless, in Scenario 2 merchants are required to pay almost 60 per cent of the average price per transaction, versus only 40 per cent for consumers; while in Scenario 1 even fc,** is still significantly below fm. [12]
In the event that a platform's per-transaction costs exceeded its fees to merchants, these consumers would in fact be even more valuable to the platform than its ‘regular’ subscribers – since the platform, having accumulated its subscription revenue, would then be losing money for every transaction actually undertaken on its network. [13]