RDP 2009-03: Competition Between Payment Systems: Results Appendix B: Analytical Results for the Chakravorti and Roson (CR) Model
April 2009
In this appendix we briefly re-visit the results obtained by Chakravorti and Roson (2006) for their original model. To better understand the impact of competition on platforms' pricing structures in this model, it is possible to derive full analytical solutions of the model under both monopoly and duopoly, in each case with and without a price level constraint – see Gardner and Stone (2009b) for the details. As discussed below, this allows us to identify a number of additional aspects of Chakravorti and Roson's results, which in turn provide insights into the implications of prohibitions on multi-homing by either side of the market (for the modelling of competition between payment systems).
For the case of identical platforms setting symmetric fees, under monopoly or duopoly, Chakravorti and Roson numerically investigate five scenarios. Three of these are situations where the maximum per-transaction benefits to consumers and merchants are equal (τ = μ), which we concentrated on in Section 3 and which we focus on again here. For ease of reference, Chakravorti and Roson's results for these three scenarios, reported previously across Tables 1 and 2, are gathered together and repeated in Table B1.[26]
| Variable | Duopoly | Monopoly | |||||
|---|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 1 | Scenario 2 | Scenario 3 | ||
| g = 0 c = 0 |
g = 0 c = 0.5 |
g = 0.2 c = 0 |
g = 0 c = 0 |
g = 0 c = 0.5 |
g = 0.2 c = 0 |
||
| Platform fees | |||||||
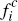 |
0.180 | 0.247 | 0.360 | 0.375 | 0.324 | 0.473 | |
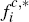 |
0.236 | 0.449 | 0.449 | 0.500 | 0.593 | 0.593 | |
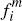 |
0.236 | 0.449 | 0.200 | 0.250 | 0.453 | 0.203 | |
| Consumer market fractions | |||||||
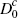 |
0.056 | 0.202 | 0.202 | 0.250 | 0.352 | 0.352 | |
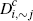 |
0.472 | 0.399 | 0.399 | 0.375 | 0.324 | 0.324 | |
| Merchant market fractions | |||||||
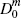 |
0.056 | 0.202 | 0.040 | 0.063 | 0.206 | 0.041 | |
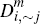 |
0.180 | 0.247 | 0.160 | 0.188 | 0.248 | 0.162 | |
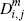 |
0.584 | 0.303 | 0.641 | 0.563 | 0.299 | 0.635 | |
| Other | |||||||
| Πi | 0.170 | 0.088 | 0.127 | 0.211 | 0.097 | 0.141 | |
| Voli | 0.361 | 0.220 | 0.319 | 0.281 | 0.177 | 0.258 | |
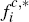 + +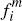 |
0.472 | 0.899 | 0.649 | 0.750 | 1.047 | 0.797 | |
| Notes: For simplicity, results are shown in units such that C and M both equal one, and the common value of τ and μ is also 1. Voli denotes the volume of transactions that take place on platform i. Notation for all other variables is as in Gardner and Stone (2009a) – see also Appendix A. | |||||||
Several of the main results observed by Chakravorti and Roson are evident in this table, including: that platforms' total effective per-transaction price level, fc,* + fm, will in every instance be lower under duopoly than under monopoly; and that the proportion of transactions occurring on either network, rather than by cash, will correspondingly always be higher with competition than under monopoly. However, a number of additional results, not explicitly noted by Chakravorti and Roson, are also apparent.
B.1 Additional Results for the Duopoly Case
Focusing first on the duopoly case, one additional result which stands out is that,
for Scenarios 1 and 2 where g = 0, symmetric competing platforms in the CR model will charge
the same fee to both merchants and consumers in per-transaction terms (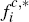 =
= 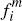 =
= 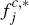 =
= 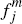 ).[27]
In fact, this is a manifestation of the following more general result – which
may, moreover, be proven rather than merely suggested numerically.
).[27]
In fact, this is a manifestation of the following more general result – which
may, moreover, be proven rather than merely suggested numerically.
Result 1. Suppose that two identical competing platforms in the CR model arrive at a symmetric, profit-maximising Nash equilibrium which is not a corner solution of the platforms' optimisation problem. Then the (common) fees charged by each platform to consumers and merchants, in per-transaction terms, will satisfy
where subscripts have been dropped in view of the symmetry assumption and where g* denotes the per-subscriber cost to platforms expressed in per-transaction terms.
The proof of this result is provided in Gardner and Stone (2009b). Here we content ourselves with four observations about it, three brief and the fourth more substantial.
The first is that it is easily checked that Equation (B1) does indeed hold not just for Scenarios 1 and 2 in Table B1, but also for Scenario 3 with g > 0. The second is that Equation (B1) implies that in the CR model, under symmetric duopoly competition, the difference between platforms' consumer and merchant fees in per-transaction terms, fc,* – fm, will be independent of the common per-transaction cost c faced by each platform to process transactions. Note, however, that this does not mean that platforms' balancing of their fees between the two sides of the market, reflected in the ratios fc,*/(fc,* + fm) and fm/(fc,* + fm), will be invariant as c changes. These ratios will typically vary with changes in c, since such shifts will generally alter the total price level, fc,* + fm, which platforms will charge to the two sides in symmetric duopoly.[28]
A third observation about Equation (B1) is that it formally quantifies various observations in Chakravorti and Roson (2006) about how symmetric, competing platforms' allocations of their fees between consumers and merchants will depend on the relative values of τi Ξ τj Ξ τ and μi Ξ μj Ξ μ.[29] Chakravorti and Roson's findings do not indicate the precise way in which fc,* and fm will vary relative to each other in the symmetric setting, as functions of τ and μ – something which Result 1 makes explicit, at least for the duopoly case.
Finally, a fourth and more substantial observation about Result 1 is that it also illustrates how pervasive the implications of a single-homing condition can be for the modelling of payments markets – an issue with potentially wider relevance than just the CR model. To see this, observe that in the event that τ = μ and g = 0, Result 1 implies that platforms in symmetric duopoly in the CR model will always (as seen in Scenarios 1 and 2) set fees such that
This symmetric treatment of the two sides of the market is actually, at first glance, surprising. After all, in the CR framework there are three ways in which the model would appear to be asymmetric (even for τ = μ and g = 0) in its treatment of consumers and merchants:
- consumers face a flat fee for subscribing to either platform but no per-transaction fees, whereas merchants face per-transaction fees for using either network but no flat fees;
- consumers are assumed to have full control, and merchants no say whatsoever, over the choice of payment method at the moment of sale; and
- consumers, unlike merchants, are prohibited from multi-homing.
Any or all of these factors might have been expected to generate some bias in platforms' treatment of the two sides of the market, even where the platforms are themselves completely symmetric. To see why they do not, consider each in turn.
On the nature of each platform's fees to the two sides of the market, what Equation
(B2) highlights is that in the CR framework the distinction between flat and
per-transaction fees to consumers is actually an artificial one. For given
merchant fees, {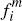 ,
,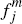 },
the number of merchants who will accept each platform's cards is fully
determined, and this information is assumed to be known to both consumers
and platforms. Thus, for any given flat consumer fees, {
},
the number of merchants who will accept each platform's cards is fully
determined, and this information is assumed to be known to both consumers
and platforms. Thus, for any given flat consumer fees, {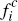 ,
,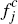 }, both platforms and
consumers in the model will know, in view of the single-homing restriction
on consumers, exactly what these fees correspond to in per-transaction terms,
{
}, both platforms and
consumers in the model will know, in view of the single-homing restriction
on consumers, exactly what these fees correspond to in per-transaction terms,
{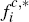 ,
,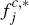 },
uniformly for all consumers; and conversely, were platforms instead setting
purely per-transaction fees for consumers, both platforms and consumers would
know what these fees would correspond to in terms of a uniform flat subscription
fee for each platform. Hence, although the CR model is nominally set up in
terms of flat fees to consumers, it can be viewed as equivalent to one in
which both sides are charged on a purely per-transaction basis. This explains
why the first of the three factors mentioned above does not, in fact, give
rise to any asymmetry between platforms' treatment of consumers and merchants
in the model.
},
uniformly for all consumers; and conversely, were platforms instead setting
purely per-transaction fees for consumers, both platforms and consumers would
know what these fees would correspond to in terms of a uniform flat subscription
fee for each platform. Hence, although the CR model is nominally set up in
terms of flat fees to consumers, it can be viewed as equivalent to one in
which both sides are charged on a purely per-transaction basis. This explains
why the first of the three factors mentioned above does not, in fact, give
rise to any asymmetry between platforms' treatment of consumers and merchants
in the model.
The second factor, however, seems more problematic. Whether one would expect the fact that consumers hold the final choice of payment instrument at the moment of sale to lead platforms to favour them in their pricing, or instead to favour merchants, is an issue we discussed in Section 5. Either way, however, one might expect it to create an asymmetry in pricing between consumers and merchants.
It turns out, however, that the imposition of a ‘no multi-homing’ condition on the consumer side in the CR model actually renders null consumers' assumed control over the choice of payment instrument at the moment of sale. There is, therefore, no aspect of the CR model which would be altered if merchants instead held the choice of payment instrument at the moment of sale.
To see this, suppose that both consumers and merchants knew, even before making their card holding/acceptance decisions, that merchants held the choice of payment instrument at the moment of sale. Since merchants face only per-transaction fees, this would not alter the card acceptance decisions of any merchant relative to the usual CR model. These decisions would continue to be based purely on whether or not each platform's cards offered a net per-transaction benefit to the merchant – with each merchant continuing to have no incentive to steer consumers (now because they hold the power over the choice of payment instrument at the moment of sale, rather than because the prohibition on consumer multi-homing removes any scope for such steering).
Moreover, consumers' card holding decisions would then also be unaltered relative
to the usual CR model. Each consumer would know: the number of merchants who
will accept each platform's cards, for any given merchant fees {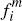 ,
,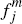 };
and that, whatever card they choose to hold (if any), every merchant that
accepts that card will prefer to choose it over cash at the moment of sale,
exactly as they themselves would do. Hence, the incentives facing consumers
in their card holding choices would also be exactly the same as in the usual
CR model.
};
and that, whatever card they choose to hold (if any), every merchant that
accepts that card will prefer to choose it over cash at the moment of sale,
exactly as they themselves would do. Hence, the incentives facing consumers
in their card holding choices would also be exactly the same as in the usual
CR model.
In the CR framework, therefore, granting the final choice of payment instrument to merchants, rather than consumers, would not alter either merchants' card acceptance or consumers' card holding decisions. Nor would it alter the model in any way in an ex post sense (since consumers hold at most one card, and merchants will always – like consumers – prefer a card payment to cash where possible). This explains why the second of the three factors mentioned above also fails to give rise to any asymmetry between platforms' treatment of consumers and merchants – as well as highlighting again how far-reaching the implications of a prohibition on multi-homing, even for just one side of the market, can be.
Finally, the third potential source of asymmetry in platforms' treatment of consumers and merchants was the prohibition on multi-homing by consumers but not merchants. Here the interesting point is that, unlike the first two factors, this does represent a genuine source of asymmetry. This is illustrated by the results for Scenarios 1 and 2 in Table B1 for the monopoly setting.
In that setting, even with τ = μ and g = 0 the monopoly operator's preferred pricing treats merchants and consumers differently in both scenarios, being tilted in each case in favour of merchants and against consumers. Hence, it appears to be a particular artefact of duopoly competition in the CR model, rather than some more general consideration, which prevents this last factor from generating any actual asymmetry in platforms' pricing, in the symmetric duopoly setting.
B.2 Additional Results for the Monopoly Case
Turning briefly to the monopoly case, we note that we can also derive a counterpart to Result 1, as follows.
Result 2. Suppose that the two platforms in the CR model are identical and that a monopoly operator selects symmetric fees for the two so as to maximise the monopolist's combined profit. Then, in the event these fees represent a non-corner solution of the monopolist's optimisation problem, the fees charged by each platform to consumers and merchants, in per-transaction terms, will satisfy
where subscripts have again been dropped in view of the symmetry assumption.
The proof of this result – which, as for the duopoly case, represents only one part of our full analytic solution of the CR model in the monopoly setting – is again provided in Gardner and Stone (2009b). Here, besides noting that it may be readily checked to hold for the three scenarios considered in Table B1, various points could again be observed about the implications of Equation (B3). For example, it implies that in the symmetric monopoly setting the quantity fc,* + 2fm will be independent of the flat cost to platforms, g, of signing up consumers. Rather than explore such observations here, however, we turn to a different issue in relation to the CR model.
B.3 The Impact of Competition on Platforms' Price Structures
As already noted, Chakravorti and Roson (2006) demonstrated that competition between two identical platforms will drive down the total combined per-transaction prices charged by each to consumers and merchants. A separate question, however, is whether competition may also cause the allocation of this total price to be even more skewed against one side of the market than would be the case with a monopoly operator of the two platforms.
To answer this question within the CR model we do not want to simply compare the proportions of total price allocated by platforms to (say) merchants in the cases of symmetric duopoly and monopoly, for given values of the parameters τ, μ, g and c. This is because, given such values, the total price levels adopted by platforms in the two settings will typically be different.
To overcome this problem one natural approach is to consider corresponding scenarios (in terms of the parameters τ, μ, g and c) under both symmetric monopoly and duopoly – with an additional condition imposed that the total per-transaction price charged in each setting is exogenously fixed at some common level, k. With this restriction in place we can directly compare how platforms will allocate their fees between merchants and consumers under monopoly versus duopoly.
For such a comparison, it turns out that – at least in the case where platforms face no cost in signing up new cardholders – one can prove the following result for the CR model in the symmetric case.[30]
Result 3. Suppose the two platforms in the CR model are identical and are restricted to charging a fixed total per-transaction price, k. Suppose also that the (common) cost to each platform of signing up new cardholders, g, is zero. Then competing platform operators in the case of symmetric duopoly will always skew their allocation of the total per-transaction price more strongly against merchants than will a monopoly operator setting profit-maximising symmetric fees for the two platforms. This will be the case for any choices of the remaining key model parameters τ, μ and c, provided these give rise to non-corner solutions of the platforms' optimisation problems in both the monopoly and duopoly settings.
Hence, at least in the case where g = 0, platform competition will always shift symmetric platforms' price structures in favour of consumers and against merchants in the CR model, relative to the situation under monopoly.
Footnotes
The CR model results shown in Table B1 actually differ at times in the third decimal place from those, based on model simulations, reported in Chakravorti and Roson (2006). This just reflects that, by virtue of having derived analytic solutions to the CR model under both monopoly and duopoly, we can determine results for these scenarios to arbitrary precision. [26]
One reason this may not have been remarked upon in Chakravorti and Roson (2006) is that, for their simulation results, they focus only on platforms' flat fees to consumers, fc, and do not report these flat fees converted to per-transaction terms, fc,*. [27]
This latter point can be established rigorously using the complete analytical solution for platforms' profit-maximising fees under duopoly in the CR model – for the case of non-corner solutions – as derived in Theorem 2 of Gardner and Stone (2009b). It is illustrated informally by a comparison of Scenarios 1 and 2. [28]
Chakravorti and Roson refer to τ and μ as determining the degree of ‘competitive pressure’ on each side of the market, and note various findings regarding how the relative competitive pressure on the two sides will affect platforms' pricing allocations in their model. [29]
As usual, see Gardner and Stone (2009b) for a formal proof of this result. Note also that we expect this result may continue to hold for many, if not all, values of g > 0. However, we are not yet able to prove a general result along these lines. [30]


