RDP 2009-03: Competition Between Payment Systems: Results 2. A Brief Recap of the CR and ECR Models

Before turning to the results from our ECR model of payment system competition, and its precursor the CR model, we briefly recap the key features of these models – a more detailed discussion is provided in Gardner and Stone (2009a). Note also that, throughout the remainder of this paper, we adopt the notation set out in Section 2 of that paper to denote key model quantities such as platform fees and consumer and merchant market fractions. For ease of reference, a table summarising this notation is provided in Appendix A of this paper.

2.1 Key Features of the CR and ECR Models

Both the CR and ECR models contain three types of agents: a set of C consumers, denoted Ω^c, a set of M merchants, denoted Ω^m, and the operators of two payment platforms, i and j. These platforms offer card payment services to consumers and merchants, in competition with the baseline payment option of cash.^[5]

Each consumer is assumed to make precisely one transaction with each merchant, using either cash or one of the platforms' cards.^[6] For a transaction to be made using a particular payment type two conditions must be satisfied.

First, both the consumer and merchant must have access to that instrument – so that, for a transaction to occur on (say) platform i, the consumer must hold a card from platform i and the merchant must accept platform i's cards. Second, the decision must be made to select that payment method in preference to other feasible options. Consistent with most treatments of payment sytems, this choice at the moment of sale is assumed to fall to the consumer. All consumers and merchants are assumed to hold/accept cash, so that cash is always a payment option.

The two platforms are assumed to face per-transaction costs of c_i for platform i and c_j for platform j, and to incur fixed costs g_i and g_j respectively for each consumer that they sign up. In terms of pricing, platforms charge flat fees, 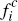and 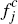to each consumer, but levy no per-transaction fees on consumers (and offer no per-transaction rewards). Conversely, platforms impose no flat, up-front fees on merchants, but charge per-transaction fees 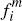and 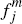to merchants for the use of their cards. Platforms are assumed to be profit-maximising.

Consumers are assumed to receive a per-transaction benefit for paying by non-cash means, equal to 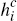for payments made over network i and 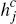for payments made over network j.^[7] Consumers are heterogeneous in their benefits, which throughout this paper are assumed to be randomly and independently drawn from uniform distributions over the intervals [0,τ_i] for platform i and [0,τ_j] for platform j.^[8]

In making their decisions about which cards to hold and use, consumers are assumed to maximise utility. Each consumer's total utility is taken to be the sum across all transactions of their benefit accrued on each, less any flat fees paid. In assessing this utility, each consumer is assumed to have a good understanding not only of the flat subscription fees charged by each platform, but also of the fraction of merchants who will choose to accept each platform's cards for given platform fees {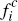,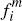} and {,}.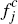

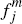In our ECR model we assume that each consumer can choose to hold no cards, one card or cards from both networks; and, if they hold both, they can choose to use card i in preference to card j, or vice versa, where a merchant accepts both. By contrast, in the CR model consumers are assumed to be prohibited by fiat from holding more than one platform's card.

Like consumers, merchants are assumed to receive a per-transaction benefit for accepting non-cash payments, equal to 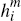for payments received on network i and 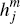for payments received on network j. Merchants are also heterogeneous in these benefits, which are again assumed to be randomly and independently drawn from uniform distributions, this time over the intervals [0,μ_i] and [0,μ_j] for platforms i and j.

In both the ECR and CR models it is assumed that each merchant can choose to sign up to both networks, one network, or neither network. Merchants make this choice based on maximising the total net benefit they will receive from doing so, taken to be the sum across all transactions of whatever per-transaction benefit they receive less any per-transaction fee charged. In assessing this, each merchant is once again assumed to have a good knowledge of both: the fraction of consumers who will sign up to each platform, for given platform fees {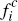,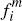} and {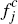,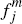}; and the fractions of those choosing to hold both cards who will then prefer to use card i over card j, or vice versa, at the moment of sale.

2.2 Implications of the ‘No Consumer Multi-homing’ Assumption in the CR Model

It may seem from this description that the differences between our ECR model and the CR model are not great, since they are identical in all respects except for their handling of potential multi-homing by consumers. The discussion in Section 3.3 of Gardner and Stone (2009a), however, already highlighted how far-reaching the consequences are of prohibiting multi-homing by consumers, as imposed in the CR model. In Appendix B we present additional results for the CR model which both augment those in Chakravorti and Roson (2006) and further draw out this point.

We obtain these additional results by deriving full analytical solutions of the CR model – under both monopoly and duopoly, and in each case with and without a constraint on platforms' total fees to consumers and merchants (in effective per-transaction terms). These analytical results complement the simulation-based analysis provided in Chakravorti and Roson. In addition to any intrinsic interest they might have, they illustrate how pervasive the effects of a prohibition on multi-homing on one side of the market can be. In particular, we use them to demonstrate that such a prohibition can vitiate not only the distinction between flat and per-transaction pricing by platforms, but also the distinction between which side of the market (consumers or merchants) holds the choice of payment instrument at the moment of sale. Given the frequent use in the literature of models in which, to simplify the analysis, one or both sides are prohibited from multi-homing, these observations may be of broader relevance than just the CR model.^[9]

Footnotes

For simplicity of exposition we take these payment systems to be card networks, but our analysis would apply just as well to non-card payment systems. [5]

By fixing the number of transactions, independent of the pricing decisions of the platforms, this assumption is consistent with the ‘derived demand’ aspect of payments. However, it also explicitly rules out ‘business stealing’ considerations from both models (see Section 1 of Gardner and Stone 2009a). [6]

Both merchants and consumers are, for simplicity, assumed to receive zero benefit if cash is used to make a payment. Also, for each consumer, the quantities {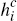,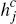} do not vary from transaction to transaction. [7]

This assumption of uniform and independent distributions was also used in Chakravorti and Roson (2006). It represents an interesting case and one which significantly simplifies analysis of the model. Note also that, since consumers' per-transaction benefits from using either platform are always non-negative, and they face no per-transaction fees, once consumers have chosen which cards to hold (if any) they will always prefer to pay by card than by cash, whenever possible. [8]

Examples of papers which focus, partly or wholly, on models where multi-homing is prohibited on at least one side include Caillaud and Jullien (2001) and Armstrong and Wright (2007). [9]