RDP 2009-03: Competition Between Payment Systems: Results 4. Another Model
April 2009
In this section we pursue further the relationship between consumers' propensity to single-home and competing platforms' pricing to this side of the market. In Section 3.1 we observed that the usual relationship found in the literature – that competing platforms will price more favourably to consumers the greater their propensity to single-home – is overturned in our ECR model.
We now develop a third model of competing payment systems, equivalent to our ECR model except with per-transaction rather than flat pricing to consumers. We henceforth refer to this as our PTP (Per-transaction Pricing) model, to distinguish it from our ECR model. We use this model to explicitly test our hypothesis that it may be the presence of flat rather than per-transaction pricing which accounts for the usual relationship described above being overturned in our ECR model.
4.1 A Model with Purely Per-transaction Pricing
Our new PTP model continues to allow for endogenous multi-homing on both sides of the market, but reverts to the more common assumption in the literature of purely per-transaction pricing by platforms to both consumers and merchants.[14] Fortunately, deriving the geometric frameworks to describe the aggregate card holding and acceptance decisions of consumers and merchants in this setting is much more straightforward than was the case for our ECR model.
We adopt the same notation used for our ECR model – with the exception that,
as there are now no flat fees 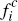 and
and 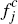 to consumers, we take
to consumers, we take 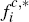 and
and 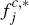 to denote the per-transaction
fees to consumers now directly set by each platform. Then, since platforms'
pricing to merchants in our ECR model was also on a purely per-transaction
basis, the geometric framework describing the aggregate behaviour of merchants
here will actually be exactly the same as there (see Appendix A
of Gardner and Stone 2009a for the detailed derivation). By this we mean that, for
given {
to denote the per-transaction
fees to consumers now directly set by each platform. Then, since platforms'
pricing to merchants in our ECR model was also on a purely per-transaction
basis, the geometric framework describing the aggregate behaviour of merchants
here will actually be exactly the same as there (see Appendix A
of Gardner and Stone 2009a for the detailed derivation). By this we mean that, for
given {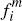 ,
,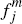 }, this framework will
look exactly like that shown in Figure 1 of Gardner and Stone (2009a) –
repeated in Panel 1 of Figure 1 of this paper – with the slopes of Lines
1 and 2 given by the same equations in terms of the consumer market fractions
}, this framework will
look exactly like that shown in Figure 1 of Gardner and Stone (2009a) –
repeated in Panel 1 of Figure 1 of this paper – with the slopes of Lines
1 and 2 given by the same equations in terms of the consumer market fractions
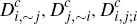 and
and 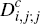 .[15]
.[15]
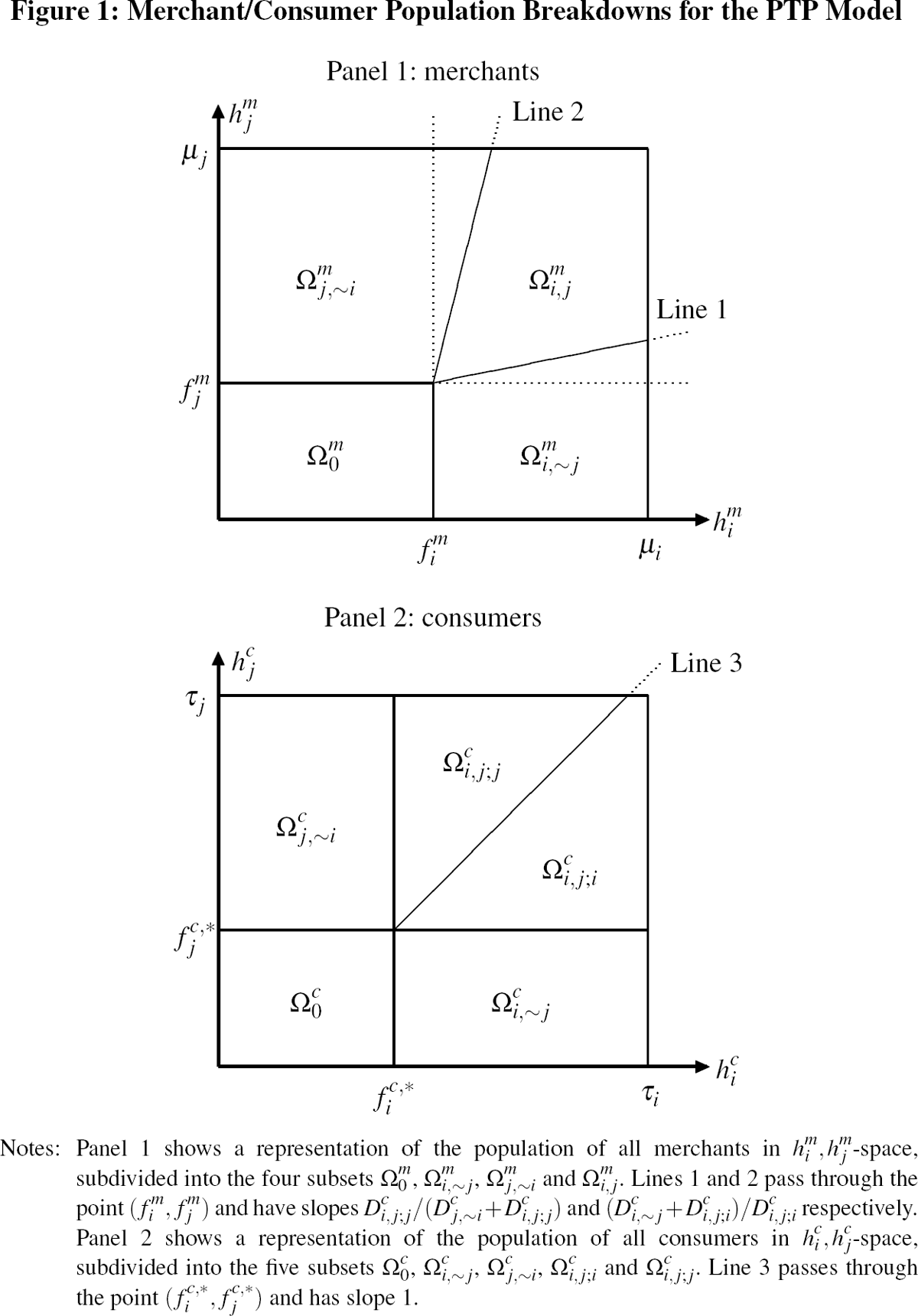
As for the geometric framework describing the aggregate behaviour of consumers, in
our PTP model consumers' costs and benefits from the use of either platform's
cards are now both determined on a purely per-transaction basis. Hence, since
it is they rather than merchants who choose the method of payment at the moment
of sale – so that no considerations of ‘steering’ arise
– consumers will clearly choose to subscribe to a platform if and only
if their per-transaction benefit from transacting on that platform exceeds
the per-transaction consumer fee set by it. Moreover, those opting to subscribe
to both platforms will clearly prefer to use card i over card j, when given the choice, if and only if the
net benefit from doing so, (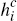 –
– 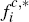 ), exceeds that from
using card j, (
), exceeds that from
using card j, (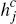 –
– 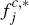 ). Hence, the population
of all consumers will simply subdivide in their card choices as shown in Panel
2 of Figure 1 – with the line dividing
). Hence, the population
of all consumers will simply subdivide in their card choices as shown in Panel
2 of Figure 1 – with the line dividing 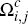 into
into 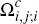 and
and 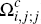 having slope 1 and
passing through the point (
having slope 1 and
passing through the point (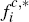 ,
,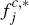 ).
).
This new model – like the CR model – can be solved analytically in the symmetric case. The theoretical details are available in Gardner and Stone (2009b). Rather than go over these here, however, we next record a number of additional observations about our PTP framework, before turning to the results which flow from it about platforms' pricing to consumers and merchants.
4.2 Three Further Observations
In this section we make three further brief observations about the PTP model just
described. The first is that, for this model, no issue of potential non-uniqueness
arises in relation to the consumer and merchant market outcomes for given
platform fees. As was discussed in detail in Section 4 of Gardner and Stone (2009a), for some
platform fee choices such non-uniqueness can arise in our ECR model. Here,
however, it cannot owing to the fact that consumers face only purely per-transaction
pricing and benefits. In combination with their holding the choice of payment
instrument at the moment of sale, this removes any feedback from merchant
behaviour into consumers' card holding choices. Hence, the breakdown of
the consumer side of the market is uniquely determined for any given platform
fee choices {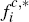 ,
,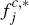 }; and this, in turn,
uniquely fixes the breakdown of the merchant side, for any given {
}; and this, in turn,
uniquely fixes the breakdown of the merchant side, for any given {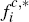 ,
,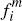 ,
,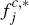 ,
,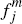 }.
}.
A second feature of our PTP framework concerns its similarity to the CR model. While it obviously differs (by construction) from our ECR model in only one way – namely the use of per-transaction rather than flat pricing by platforms to consumers – it turns out that it also differs from the CR model in only one respect. For although the CR model is formally set up in terms of platforms charging flat fees to consumers, it is actually equivalent (as discussed in Appendix B) to a model in which both sides of the market are charged purely per transaction. Hence, the CR model is actually identical to our PTP model, save for the restriction that consumers in the CR model may at most subscribe to the cards of a single platform.
Finally, a third point about our PTP model is that it may actually be viewed as a special case of a more general model, incorporating an additional parameter κ.
This parameter represents the disutility to a consumer from holding more than one card – say, due to the cluttering of their wallet, or the hassle of having to check multiple periodic transaction statements. The option of including such a parameter was raised in relation to our ECR model, but not pursued there (see Section 3.3 of Gardner and Stone 2009a). In Section 5, however, it will be useful to take up this option in the context of our PTP model – as well as the option of then varying which side of the market, consumers or merchants, is assumed to hold the choice of payment instrument at the moment of sale.
4.3 Revisiting the Relationship between Platform Pricing and Consumers' Propensity to Single-home
We now turn to the simulation results which may be obtained from our PTP model. For the duopoly case, these were already shown in Table 1 for the three scenarios considered earlier.
In discussing these results we focus primarily on the price allocation aspects of platforms' fee choices. It is worth noting first, however, that the total price level charged by competing platforms in the PTP model, for both Scenarios 1 and 2, is higher than for either the CR or ECR model. Hence, when both sides of the market can multi-home, the use of purely per-transaction pricing allows platforms in these scenarios to extract markedly higher revenue per transaction – which in these cases also translates into higher profits relative to the CR and ECR models.
Greater average per-transaction revenue need not always lead to higher platform profits, however, as the results for Scenario 3 illustrate. Although AvgPPT is again higher there than for the CR or ECR models (0.708 versus 0.649), this higher revenue comes at the cost of substantially lower transaction volume (0.285 versus 0.319). With platforms here facing per-subscriber and not just per-transaction costs, this lower volume then turns out to be sufficient to make overall platform profit in the PTP model lower, for this scenario, than in the CR and ECR models (0.109 versus 0.127).
Turning now to the price allocation aspects of the results in Table 1, for all three scenarios we see that competing platforms' fees are more skewed against consumers in the PTP model than in the CR model. In the case of Scenarios 1 and 2, for example, fees to both consumers and merchants are higher in the PTP model, but the difference is greater for consumers – so that they now bear more than half of the total per-transaction price levied by platforms.[16]
In contrast to the findings in Section 3.1 from comparing the CR and ECR models, these results are consistent with the relationship previously found in the literature between competing platforms' price structures and the propensity of consumers to single-home. They suggest that, in a framework of purely per-transaction pricing, an overwhelming propensity for consumers to single-home – the only difference between the CR model and our PTP model – does imply more favourable pricing by platforms towards consumers than if the latter are more amenable to holding multiple cards.
Overall, therefore, these results formally confirm our hypothesis, in Section 3.2, that per-transaction pricing is the key driver of a positive relationship between consumers' propensity to single-home and the attractiveness of the pricing they will be offered by competing platforms. Where purely per-transaction pricing is used by platforms, our results tally with the existence of such a relationship. However, as discussed in Section 3.1, this need not hold when platforms instead levy flat fees on consumers (which is typically the case in the real world).
4.4 Multi-homing and Payment Instrument Choice
A final remark is in order regarding the relationship between the propensity to single-home and platforms' pricing. We just claimed, rather loosely, that our results confirm that where purely per-transaction pricing is used by platforms, a positive link exists between consumers' propensity to single-home and the attractiveness of the pricing they will be offered by competing platforms. These results are, however, for a world where consumers always have the final choice of payment instrument. Hence, they strictly only confirm a positive link between propensity to single-home on the side with the choice of instrument and the attractiveness of platforms' pricing to that side. The same caveat turns out to apply to the other papers in the literature reporting such a link, such as those quoted in Footnote 1.
This raises the question whether or not the more general result, loosely stated earlier, holds without this caveat. It turns out that the short answer to this is no: a positive link does not necessarily hold between propensity to single-home on the side without the choice of instrument and the relative attractiveness of platforms' pricing to that side – even when platforms' pricing is on a purely per-transaction basis. We return to the demonstration of this claim below.[17]
Footnotes
Note that this does not make the model an entirely ‘per-transaction model’, since on the cost side it still allows for platforms to incur costs gi and gj which are per-subscriber rather than per-transaction. Only in the event gi = gj = 0 will the behaviour of all agents in our new model be determined completely by per-transaction considerations. [14]
Of course, the actual values of these consumer market fractions – and hence
the slopes of these two lines – will typically differ between our
PTP and ECR models, even in the event that the fees {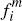 ,
,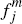 ,
,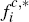 ,
,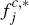 }
happen to coincide in the two.
[15]
}
happen to coincide in the two.
[15]
In the case of Scenario 3 this difference is even more marked, in that platforms' per-transaction fees to merchants are actually lower in the PTP model than in the CR model, whereas fees to consumers are much higher. [16]
In fact, this claim can already be verified, for the case g = c = 0, from the results in Table 1. In this case: (i) the only asymmetry between the two sides in our PTP model relates to who holds the final choice of instrument, so that the results for this model with consumer choice replaced by merchant choice would actually be exactly the same as those shown for Scenario 1, except with the roles of consumers and merchants reversed; and (ii) as discussed in detail in Appendix B, the CR model is actually equivalent to a PTP model with merchant rather than consumer choice (together with an overwhelming predisposition on the part of consumers to single-home). Looking at the results for Scenario 1 in Table 1 then shows that: when consumers have no particular innate propensity to single-home and merchants choose (PTP model with consumers and merchants switched), consumers must bear only around 45.5 per cent of the total per-transaction price charged by platforms to both sides (fc,* = 0.262, fm = 0.314); whereas when they have an overwhelming innate propensity to single-home and merchants choose (CR model), consumers must bear half of platforms' total per-transaction price (fc,* = fm = 0.236). Hence, in this case a greater predisposition to single-home by the side without the choice of instrument does not translate into more attractive relative pricing by the platforms to that side (even though it does improve the absolute pricing by competing platforms to consumers). [17]