RDP 2008-09: A Term Structure Decomposition of the Australian Yield Curve 5. Results
December 2008
- Download the Paper 579KB
We estimate the model over two time horizons. First we use all available data so that our sample runs from July 1992 to April 2007. Then we restrict the sample to the period July 1996 to April 2007. This shorter sample covers the period when inflation expectations have been reasonably stable and consistent with the Reserve Bank's inflation target, and corresponds to a period of stable growth and low inflation. (In both cases we use the first six months of data to estimate the latent factors, but discard it when estimating model parameters.)
5.1 The Period 1993 to 2007
The primary variables of interest are the estimated expected future short rates and term premia, which are shown in Figure 2.
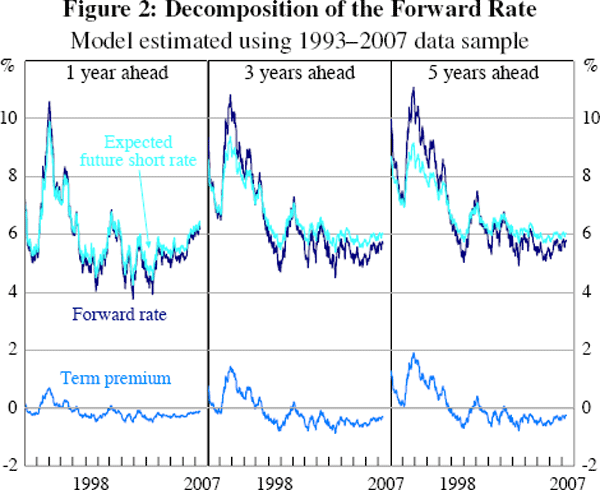
As expected, the forward rate and the expected future short rate tend to track each other closely at the 1-year time horizon, while at longer horizons they diverge, with more substantial positive and negative term premia emerging. Estimated term premia peak around 1994–1995, a period when inflation, inflation expectations and interest rates were all rising and economic growth was somewhat volatile. Term premia then fell steadily until around 1998, before increasing again over the next year or two. The period 1999–2000 saw a marked slowdown in global economic growth, a rise in inflation and bond yields, and a depreciation of the Australian dollar from around US 65 cents to around US 50 cents. From around 2001 to the end of the sample, term premia have been fairly steady.
Figure 2 shows that expected future short rates are more stable than the forward rate, so that term premia tend to increase when yields are rising and decrease when yields are falling, especially for the longer-horizon samples. This result sits well with economic intuition. It seems obvious that market participants' view of the overnight cash rate a few years hence should be relatively stable – bullish macroeconomic news that would perhaps imply an increased chance of a near-term monetary tightening may raise the market's forecast of short-term interest rates, but its effect on expected interest rates years into the future is likely to be relatively small. Despite this, yields on long-term government bonds do react to such news, and to a greater extent than may seem warranted purely by changing forecasts of the real economy. As such, variations in long-term bond yields seem to be partly driven by factors other than expected future short rates, and these other factors show up as term premia in our model.
An alternate explanation raised in the literature is that this phenomenon is model driven, since the amount of variation seen in expectations of the future short rate far into the future can be significantly affected by the K matrix. In particular, large diagonal entries in the K matrix imply fast mean reversion of latent factors. This in turn means that expected future short rates will revert to the long-run value, ρ, very quickly, so that while yields may move, expected future short rates will vary little. However, this does not seem to affect our results (see discussion of the K matrix below).
Another interesting consideration is the fall in term premia, particularly pronounced between 1996 and 1998, and its subsequent stabilisation. Again, this is to some extent a function of falling yields and more stable expected future short rates. On the other hand, notwithstanding the preceding discussion, there is nothing in the model which forces term premia, as opposed to expected future short rates, to fall. It is also interesting to note that the up-ticks in term premia associated with higher inflation become more muted as time progresses. For example, underlying inflation peaked at similar levels during the periods 1994–1995, 2000–2001 and 2005–2006, yet in each case the response from term premia was very different – in the first period term premia rose by roughly 2 percentage points, in the second period by half a percentage point, and in the third period not at all (1999 also saw inflation rising, and term premia up by around 1 percentage point, but inflation peaked at a lower level than in the other three cases). The fall in the general level of term premia, and the more muted response of term premia to economic shocks, coincides with a period of relatively stable inflation and economic growth, and may reflect growing credibility of the Reserve Bank's inflation target among financial market participants. These factors undoubtedly affected both yields and term premia, making it difficult to establish causality, but it is nonetheless clear that our model-implied term premia behave as we might expect over this period.
The sustained negative term premia in the latter part of the sample is an interesting result of the model. Studies for other countries have also found negative term premia, although not to the same extent as our results. It is possible that model misspecification could be partly responsible for the size of the negative term premia, with the model placing the short rate too high and therefore term premia too low (we return to this point below). Alternatively, Australia's relatively small supply of government bonds may have resulted in yields being bid down by risk-averse and mandate-constrained investors. Indeed, over the latter part of the sample, government bond yields consistently implied lower forward rates than those seen in analysts' forecasts of the cash rate. From late 2000 to the end of the sample, bond yields have, on average, implied 2-year forward rates which are around half a percentage point below those seen in analysts' forecasts. Bond-implied forward rates were briefly above analysts' forecasts of the cash rate in 2002, when positive term premia were last seen. Over 2006 and 2007, the differential (while negative) narrowed, which also accords with our model estimates that show term premia tending slowly towards zero over the period.
In general, by allowing a flexible specification of term premia we also allow negative term premia to arise; these are in any case relatively small and have occurred over a period for which it is not inconceivable that negative term premia of the magnitude estimated indeed existed. We also note that, given the historical variability seen in the actual cash rate over the past decade or so, the level of variability seen in our estimates of the expected future cash rate seems reasonable.
In Table 1 we present the estimated parameters of the model. Focusing first on the K matrix, consistent with Kim and Orphanides (2005), the smallest (K)ii estimated (in our case for the second latent factor) is quite small, at 0.06. In a single-factor model such a number would imply a half-life (being the time taken for a latent factor to revert half way back to its mean value of zero after experiencing a shock) of around 12.3 years (the other two half-lives would be 140 and 256 days). In term structure models such as ours, such a slow moving factor captures the longer-term characteristics of interest rates, which tend to follow the business cycle or other gradual trends, and may not mean revert for many years. Such small diagonal entries of K will improve estimation of expected future short rates at longer horizons. These estimated expectations would otherwise simply be flat and given by ρ.
| Parameter | Index number (i) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| ρ | 6.97 (0.19) | – | – |
| (K)1i | 1.81 (0.06) | 0 | 0 |
| (K)2i | −0.79 (0.04) | 0.06 (0.00) | 0 |
| (K)3i | 23.99 (0.50) | 4.41 (0.22) | 0.99 (0.02) |
| (Σ)ii | 0.15 (0.01) | 0.20 (0.01) | 0.42 (0.02) |
| λ0,i | −0.11 (0.02) | 0.19 (0.02) | −0.23 (0.05) |
| (Λ)1i | −324.10 (1.03) | −43.17 (0.21) | −0.01 (0.00) |
| (Λ)2i | 17.29 (0.28) | 15.75 (0.30) | 3.87 (0.05) |
| (Λ)3i | −68.11 (0.22) | 82.39 (0.58) | −10.69 (0.38) |
| Notes: ρ and (Σ)ii are given in percentage points. Standard errors are shown in parentheses. | |||
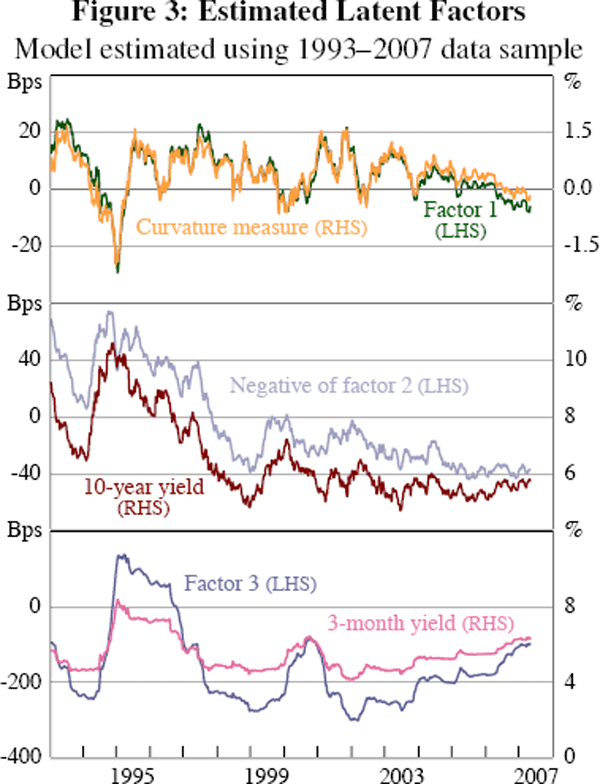
The latent factors are the processes that drive the evolution of interest rates. While they have no definitive economic interpretation, it is nevertheless interesting to examine how the model captures the yield curve with these three factors. Figure 3 displays the estimated latent factors of the model, along with various yield curve measures. The first latent factor is highly correlated with the curvature of the yield curve, where here we measure curvature as the 3-month yield plus the 10-year yield less twice the 2-year yield. The second latent factor exhibits a close relationship with long-term interest rates and consequently displays very slow mean reversion. This factor has a correlation coefficient of −0.96 with the 10-year yield. Finally, the third latent factor closely resembles short-term interest rates; it has a correlation coefficient of 0.98 with the 3-month yield.
Interpreting the term premia parameters is much more difficult as there are more of them and their effect on model outputs depends crucially on the sign and size of the xt latent factors. Hence it is probably more intuitive to focus on the term premia produced (Figure 2) than on the actual numbers given in Table 1.
Finally the value of the constant ρ, which gives the short rate in steady-state and is estimated at 6.97 per cent, appears a little high. As mentioned earlier, it may be that the model is placing the long-run equilibrium short rate at a higher level than is warranted, thereby contributing to persistently negative term premia. The data sample does encompass the mid 1990s, formative years for the inflation-targeting regime and a period of relatively high cash rates which may have pushed up the estimate. Note also that our model gives the short rate at any time t as ρ plus the sum of the latent factors at t, and while the latent factors decay to zero, this happens very slowly. In fact over the sample period the value of x1,t + x2,t + x3,t has averaged −1.49 per cent. As the short rate is given by ρ + x1,t + x2,t + x3,t, the equilibrium short rate over the sample could therefore be interpreted as being closer to 5½ per cent rather than to 7 per cent.
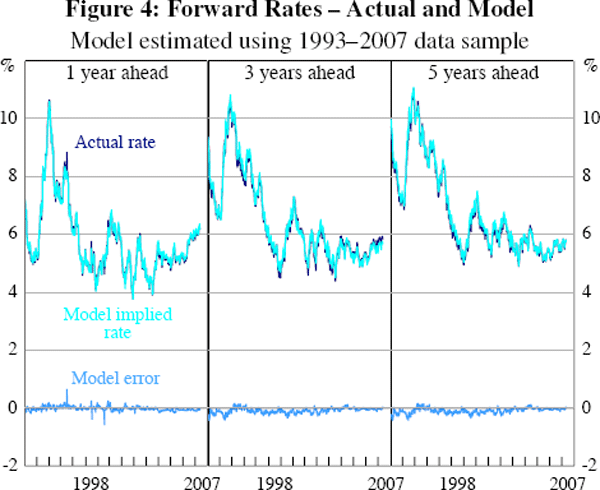
Actual and model-implied forward rates are shown in Figure 4. The fit is not perfect, but at any time the dynamic term structure model has much less flexibility in generating yields along the curve than the model used to estimate the zero-coupon yields – it must rely on the three latent factor values to generate an entire yield curve. Hence we would not expect the model to be perfect. Rather, we trust that it broadly characterises the observed actual yields, which appears to be the case – model errors are generally small and hover around zero, only departing when yields rise or fall particularly quickly.
5.2 The Period 1997 to 2007
The data sample used in Section 5.1 spans the adoption by the Reserve Bank of the 2 to 3 per cent inflation target, the decline in inflation expectations, and the formal acknowledgement of Reserve Bank independence. As a result, there may be a structural break for which the model does not account. To check the robustness of the results to this possibility we estimate the model again using a restricted sample which encompasses the more stable period from 1997 to early 2007. Although the model estimates over this shorter sample are quite similar to those for the full sample, it is interesting to compare the two.
The estimated expected future short rates and term premia are given in Figure 5. The most obvious difference between Figure 5 and Figure 2 is the more stable expected future short rates and, consequently, the more variable term premia seen in the shorter sample. This is unlikely to be related to the K matrix since the shorter sample has one latent factor which is even slower to mean revert than in the case of the longer sample. The term premia parameters Λ and λ0 are numerically larger in the short sample model indicating, all else equal, that changes in yields will have a larger impact on term premia (and so a smaller impact on expected future short rates) than in the longer sample.
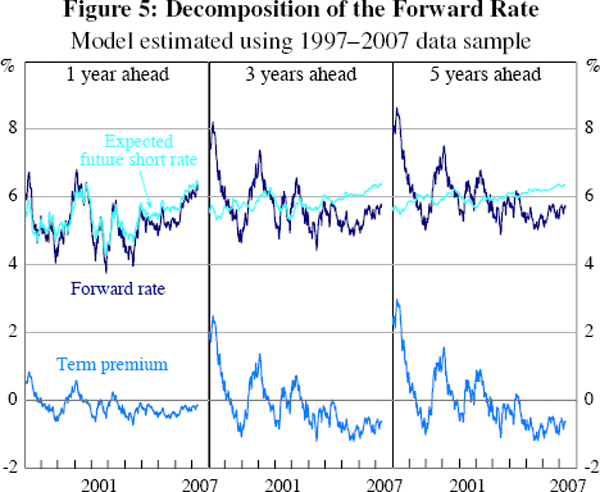
In the shorter sample model there is an apparent upward trend in short rate expectations from around 2004 or earlier. Again it is hard to determine exactly what caused this, but it did occur during a time of rising cash rates, low but rising inflation, falling unemployment and stable growth. So for the 1-year ahead forecast at least, the trend seems plausible. The trend in the 5-year ahead forecast is smaller but still apparent. However, being of the order of less than one-quarter of a percentage point, it is probably not significant given the precision of the model .
Despite differences between the models one should keep in mind that the two are actually quite similar – the differences regard the degree of certain phenomena, not their existence. In fact, the estimates produced by the two models are generally within half a percentage point of each other; by comparison, Kim and Orphanides (2005), who also estimate models over two different sample periods, find differences in the order of around 2 percentage points.
The estimated parameters of the model over the short sample are given in Table 2. Similar to the longer sample, the smallest (K)ii estimated (in this case for the first latent factor) is small at 0.01. In a single-factor model such a number would imply a half-life of around 130 years (the other two half-lives would be 94 and 459 days). The extremely slow mean reversion of the first latent factor is likely due to the short sample period used, which spans a period of strong growth and low inflation, and in particular does not span a ‘full’ economic cycle encompassing a sizeable economic downturn.
| Parameter | Index number (i) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| ρ | 6.78 (0.06) | – | – |
| (K)1i | 0.01 (0.00) | 0 | 0 |
| (K)2i | 0.55 (0.01) | 2.69 (0.04) | 0 |
| (K)3i | 2.88 (0.05) | 17.38 (0.11) | 0.55 (0.01) |
| (Σ)ii | 0.08 (0.00) | 0.15 (0.01) | 0.30 (0.01) |
| λ0,i | 1.45 (0.01) | −1.91 (0.03) | −1.06 (0.02) |
| (Λ)1i | 465.20 (0.39) | 440.07 (0.26) | 12.81 (0.09) |
| (Λ)2i | −699.87 (0.44) | −763.06 (0.48) | 1.16 (0.03) |
| (Λ)3i | −171.60 (0.21) | −396.64 (0.28) | −109.58 (0.17) |
| Notes: ρ and (Σ)ii are given in percentage points. Standard errors are shown in parentheses. | |||
Figure 6 shows that the first latent factor exhibits slow mean reversion, and is in fact highly correlated with the slope of the yield curve (correlation coefficient of −0.97). In contrast, the much faster mean reverting third latent factor is highly correlated with the 3-month yield (correlation coefficient of 0.98), while the second latent factor is correlated with both the level and the curvature of yields.
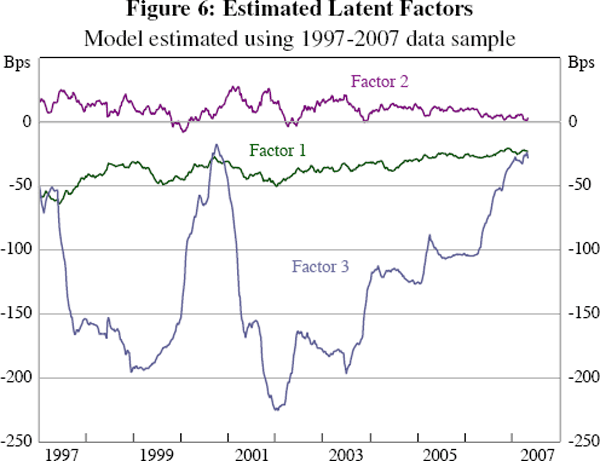
It is interesting to note that for the shorter sample model, ρ is estimated at 6.78 per cent, below the 6.97 per cent estimated for the longer sample model. As touched on earlier, the credibility of the Reserve Bank's inflation target was being tested around 1994, which resulted in interest rates, and especially long-term rates, rising quite strongly. There may therefore be a structural change in interest rate dynamics around 1995–1996, associated with the Reserve Bank's success in reducing inflation and the moderation in inflation expectations, for which the model cannot account. The fact that the estimated equilibrium short rate is lower over the shorter sample is consistent with this. The lower value of ρ also manifests itself in less persistently negative term premia than those seen in the longer sample (note that similar to the longer sample model, the sum of latent factors averaged −1.56 per cent, giving an effective estimated short rate over the period of close to 5¼ per cent).
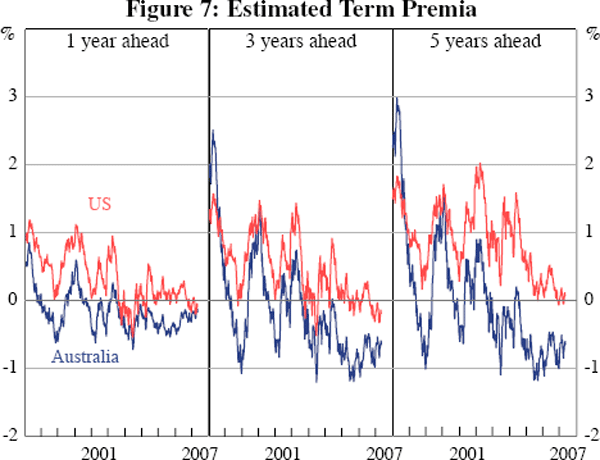
As a final point, it is interesting to compare our term premia estimates with those derived for US data. Figure 7 shows 1-, 3- and 5-year term premia as estimated by us for Australian data, as well as corresponding term premia estimated by Kim and Wright (2005), who also use the Kim and Orphanides model, for US data.[16] One can see that, excepting a level difference between the two series, the estimated Australian and US term premia track each other relatively closely – the correlation coefficient between the two series is 0.84 for the 1-year ahead term premia, 0.90 for the 3-year ahead term premia, and 0.81 for the 5-year ahead term premia. These results suggest that term premia may be driven by global, as opposed to country-specific, phenomena, as typified for example by the global ‘search for yield’ that received so much attention earlier this decade.
Footnote
Available from <http://www.federalreserve.gov/Pubs/feds/2005/200533/feds200533.xls.> [16]