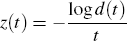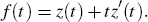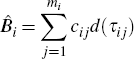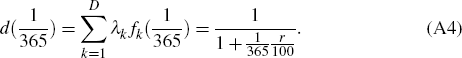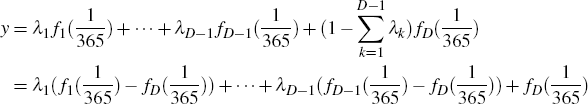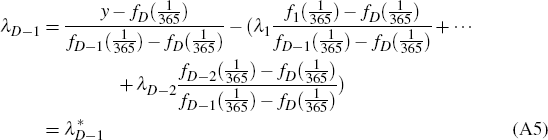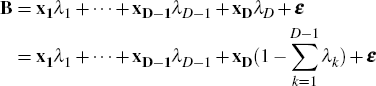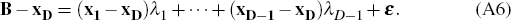RDP 2008-09: A Term Structure Decomposition of the Australian Yield Curve Appendix A: Zero-coupon Yields
December 2008
- Download the Paper 579KB
We estimate zero-coupon yields using the Merrill Lynch Exponential Spline (MLES) methodology adapted from Li et al (2001). This technique appears to be very efficient, and produces a good fit for the input data (technical details are given later in this Appendix).
The hardest data to fit is for maturities around the 1-year mark, where from early 2001 the input data for any given day transitions from OIS rates (used as input data for maturities extending up to 1 year into the future) to bond yields (used for maturities greater than or equal to 18 months into the future). Although we regard OIS rates as the closest available substitute for risk-free Treasury note yields, they are not Treasury notes – they are swap contracts as opposed to physical bonds or notes, and they trade in a different market to physical bonds or notes, which may mean that the factors affecting OIS pricing are sometimes different from those affecting note or bond pricing. That being said, the MLES procedure still provides a good fit to the data even here – the average absolute error between the 1-year OIS yield and the MLES estimated 1-year yield is around 3½ basis points; the largest error is only 12 basis points and the error is larger than 10 basis points only three times. Taking a broader perspective, the fit of the MLES method is in fact very good, with the daily mean absolute error between fitted yields and actual yields averaging less than 2 basis points, and peaking at only 6 basis points.
Another potential and related criticism is the mixing together of OIS and bond yields to estimate a single yield curve. We believe that although Treasury note yields would be preferable for short maturity data inputs, in their absence, OIS rates are the next best, and in fact a very good, substitute. They are virtually risk-free and so can sensibly be used in the estimation of our risk-free yield curve, and they fulfil a vital function in supplying information about the short end of the yield curve that would otherwise be unavailable.
In any case, given that we are fitting a flexible term structure model, so long as the evolution of OIS yields through time is comparable to the evolution of Treasury note or bond yields, any residual risk premia inherent in OIS yields should be captured as short-dated term premia in the model. Overall, while Treasury note yields would be preferable, in their absence OIS yields provide a very good substitute.
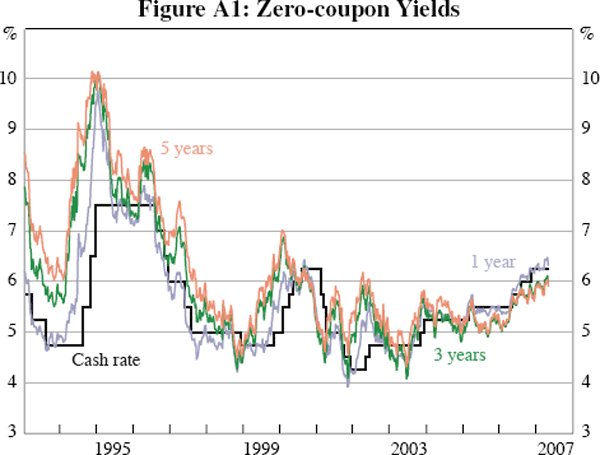
We display estimated 1−, 3− and 5-year zero-coupon yields, as well as the interbank overnight cash rate in Figure A1.
The technical details of the MLES methodology are as follows. We model the theoretical discount function d(t) as a linear combination of hyperbolic basis functions.[17] The discount function is assumed to be of the form
where D is the number of basis functions (in our case D = 8), and α is an exogenous parameter, taken as 5 per cent.
Once we have estimated the λk coefficients we have a smooth discount function. From this it is a simple matter to compute the zero-coupon yield curve, given by
and the (instantaneous) forward curve given by
Given the assumed form of the discount function, the theoretical price of bond i is given by
where cij is the jth cash flow of bond i, occurring at time τij, and mi is the number of cash flows belonging to bond i. That is, the price of bond i is the sum of its discounted cash flows.
The price of a bond is the linear sum of its discounted cash flows. The discount function is assumed to be a linear sum of basis functions. This linearity allows us to write the vector of bond prices or OIS rates B as
where BT = [B1, … ,Bn]
is the vector of observed
prices,[18]
X is a n × D matrix with 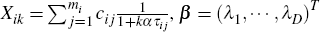 and ε
a vector of errors.
and ε
a vector of errors.
For W the weight matrix,[19] if we wished to minimise the weighted squared pricing errors εT Wε, then the solution would be given by
We wish to impose some restrictions on d(t) however: d(0), the discount rate at t = 0 should be 1, that is, one dollar today is worth one dollar. Also, the cash rate (as of today) is known and fixed, and so should be reflected in the discount function. These requirements complicate matters slightly.
From Equation (A1) it is clear that 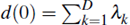 .
Hence requiring d(0) = 1 is equivalent to requiring
.
Hence requiring d(0) = 1 is equivalent to requiring 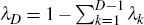 .
.
Writing 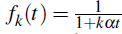 ,
we can ensure that the 1-day yield is given by the overnight cash rate, r
say, by requiring
,
we can ensure that the 1-day yield is given by the overnight cash rate, r
say, by requiring
Writing 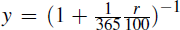 ,
from Equation (A4) these two constraints are equivalent to
,
from Equation (A4) these two constraints are equivalent to
and hence
We first impose the d(0) = 1 constraint. Writing xi for the ith column of the X matrix, Equation (A2) becomes
so that
Writing 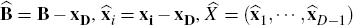 and
and 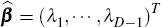 Equation (A6) becomes
Equation (A6) becomes
The estimate of 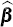 which minimises
which minimises 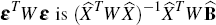 .
Hence we have found the least squares estimate of β
from Equation (A2), subject to the d(0) = 1 constraint.
.
Hence we have found the least squares estimate of β
from Equation (A2), subject to the d(0) = 1 constraint.
If we now start from Equation (A7), replace λD-1 with 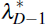 from Equation (A5)
and follow the procedure above, we obtain our estimator. In this case the
estimator of
from Equation (A5)
and follow the procedure above, we obtain our estimator. In this case the
estimator of  which solves
which solves
for 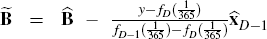 and
and 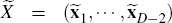 for
for 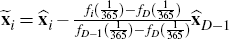 is given by
is given by
Hence we have solved Equation (A2) subject to both desired constraints.
Footnotes
The discount function d(t) gives the value today of 1 unit at time t in the future. [17]
For OIS contracts the ‘observed price’ corresponds to the price of a discount security paying the OIS yield. [18]
The weight attached to each bond is taken as its inverse duration. This has the effect of minimising fitted yield errors, as opposed to price errors. [19]