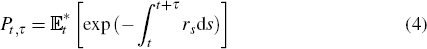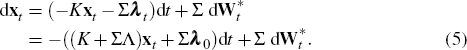RDP 2008-09: A Term Structure Decomposition of the Australian Yield Curve 3. The Model in Detail

In this section we outline the model we use. In what follows, scalars are lowercase and not bold, vectors are bold upper-case and lower-case, and matrices are upper-case and not bold. For mathematical convenience and to be consistent with the literature, the model is considered in continuous time; discrete time versions of such models are also possible.

Let r_t be the instantaneous short rate or cash rate and assume that

where and

where K is lower triangular and Σ is diagonal, both 3 × 3 matrices, and W_t is standard multivariate Brownian motion which is analogous to a continuous time version of a random walk. Equations (1) and (2) imply that the short rate is a function of a constant ρ and three time-varying (‘latent’) factors, 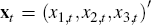, with the evolution of x_t following a zero-mean Ornstein-Uhlenbeck process, the continuous time analogue of a vector auto-regressive process. Here the drift term −Kx_tdt is the deterministic component of the stochastic differential equation, with K controlling the speed of mean reversion, and the diffusion term Σ dW_t is the random component, with the Brownian motion W_t providing random shocks to the system. As mentioned earlier, the latent factors x_t are not observable and need to be estimated with the parameters of the model.

Investors demand compensation for holding bonds, whose value depends on the random, and hence risky, latent factors; cash is free of this risk. The amount of compensation demanded is termed the market price of risk, and it is this price of risk that determines term premia (it is worth emphasising that the price of risk and term premia are not the same thing; see Section 4). We assume that the price of risk is of the form

where 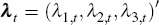, with λ_i,t the price of risk associated with the latent factor x_i,t at time t, 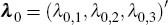and Λ a 3 × 3 matrix. This specification implies that for each i, the extra compensation demanded by investors for bearing the risk of x_i,t is comprised of a constant λ_0,i plus a linear combination of the latent factors, .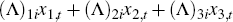

Given this model, the arbitrage-free price of a zero-coupon bond at time t, paying 1 unit at t + τ, is given by

where the expectation is taken with respect to the risk-neutral probability distribution (also referred to as the risk-neutral measure or equivalent martingale measure).^[6] The risk-neutral probability distribution adjusts the actual (real-world) probability distribution for investors' risk preferences, and so under this new distribution we can treat investors as if they were risk-neutral. This means that under the risk-neutral distribution we can price any asset by simply calculating the expected discounted present value of its future cash flows (see Appendix B for a sketch of a proof).^[7]

Equations (1) and (2) describe the dynamics of the short rate under the real-world probability distribution. To obtain the dynamics of the short rate under the risk-neutral probability distribution we subtract Σ times the market price of risk, as given by Equation (3), from the drift component of x_t, as given by Equation (2), to obtain

While W_t is Brownian motion under the real-world probability distribution, it is not Brownian motion under the risk-neutral distribution. However, W_t is related to Brownian motion under the risk-neutral probability distribution, denoted by 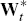, according to 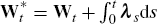, or equivalently 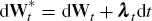, In other words, 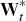is derived by adjusting W_t for the market price of risk, given by λ_t .^[8]

Given Equations (1) and (5), Duffie and Kan (1996) show that the price of a zero-coupon bond (Equation (4)) can be simplified to

where α_τ and β_τ are functions of the underlying parameters ρ, K, Σ, λ₀ and Λ (see Appendix C for details). Given that we can infer zero-coupon bond prices from government coupon bond data, we can estimate the parameters of the model by minimising the difference between zero-coupon bond prices and those prices implied by Equation (6).

Note that from Equations (1) and (2), the only parameters of the model which affect the short rate, and therefore which determine estimates of the expected future short rate, are ρ, K and Σ. On the other hand observed bond prices, as specified by Equation (6), incorporate term premia and are therefore also affected by the parameters determining the market price of risk: λ₀ and Λ. Hence in order to separate expected future short rates from term premia we need estimates of λ₀ and Λ as well as ρ, K and Σ. However, the matrices K and Λ only appear in the formulas for α_τ and β_τ (and hence only impact on bond prices) in the form (K + ΣΛ). That is, when they do appear they only appear together. This means that observed market prices in and of themselves do not identify K (which in the sense just described determines expected future short rates) separately from Λ (which likewise determines term premia).

Instead we rely on the fact that the latent factors evolve according to the real-world probability distribution as given in Equation (2), where K does appear without Λ. We also use analysts' forecasts of future interest rates, which give a clean reading on expected future short rates abstracting from term premia. As our forecast data are relatively sparse, estimates of how the latent factors x_t evolve play a large role in separating K from Λ, and these latent factors must in turn be estimated from the data.

Footnotes

See, for example, Duffie and Kan (1996). [6]

For more detail on risk-neutral probability distributions see, for example, Cochrane (2001) or Steele (2001). [7]

See, for example, de Jong (2000) or Dai and Singleton (2002). [8]