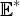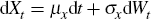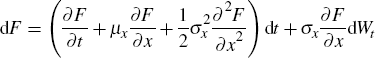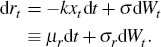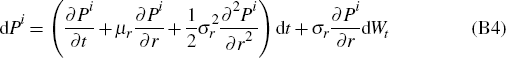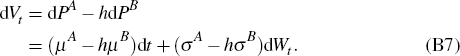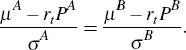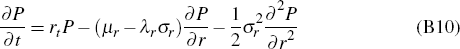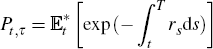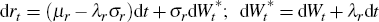RDP 2008-09: A Term Structure Decomposition of the Australian Yield Curve Appendix B: Risk-neutral Bond Pricing

Here we examine why bonds should be priced under the risk-neutral measure. To simplify the analysis we work with a single factor model, that is

where all variables are scalars.

Consider the probability space 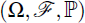with associated filtration 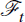taken as the augmented filtration of 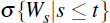(see, for example, Steele 2001). X_t is an Ito process if

for μ_x and σ_x adapted to 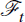. Ito's lemma then states that for any function F(x,t) such that F is twice differentiable in x and differentiable in t,

Applying Ito's lemma to Equation (B1) we trivially get

Now let P^A(r_t,t) and P^B(r_t,t) denote the time t price of two zero-coupon bonds with different maturity dates. Then by Ito's lemma, Pⁱ (i = A, B) will satisfy

Consider a portfolio that is long one A bond and short h B bonds. At time t this portfolio has value

If held for dt, the portfolio's value changes by

Hence we can make the portfolio instantaneously riskless by choosing h = σ^A/σ^B. In this case, the portfolio must earn the risk-free rate r_t and so

Substituting Equations (B6) and (B7) into Equation (B8) and setting h = σ^A/σ^B leads to

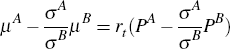
or

Hence the ratio (μ − r_tP)/σ is independent of the choice of bond, and so there must exist a function λ_r such that

holds for any bond price P.

Now substituting μ and σ as identified by Equations (B4) and (B5) into Equation (B9) results in a Black-Scholes type partial differential equation

which is solved subject to appropriate boundary conditions (bonds pay 1 unit at maturity) and the radiation condition P → 0 as r → ∞.

The Feynman-Kac formula then says that the solution to Equation (B10) is given

where r_t satisfies

and 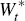is standard Brownian motion in the risk-neutral measure associated with