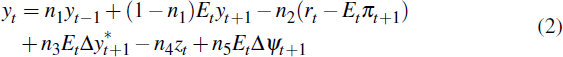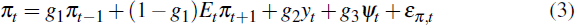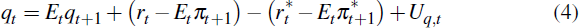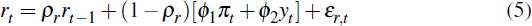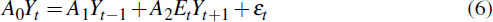RDP 2008-08: The Role of International Shocks in Australia's Business Cycle 3. A Small Open Economy DSGE Model
December 2008
- Download the Paper 373KB
This section presents the estimated small open economy DSGE model. The model is based on a slightly modified version of that proposed by Monacelli (2005) and Galí and Monacelli (2005). The set of estimated parameters is used to simulate Impulse Response Functions (IRFs) to provide a set of robust sign restrictions for the VAR analysis. The model consists of an open economy IS equation and a Phillips curve incorporating imperfect exchange rate pass-through. The monetary authority sets interest rates according to a Taylor-type reaction function, while the exchange rate depends on the interest rate differential between the domestic and foreign economies. The variables for the rest of the world are taken to be exogenous processes.
The open economy IS equation derived from the consumer's optimising problem is:
where: n1,..., n5 are parameters; yt
is the aggregate output gap; rt is the nominal interest
rate; πt is the inflation rate; 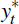 is the foreign output
gap; and zt represents technology disturbances that follow
an AR(1)
process.[5]
Ψt = (1 — γ)st
— qt can be interpreted as the law of one price gap
which measures the deviation of the domestic price of imported goods from the world
price, where st is the terms of trade, defined
as export prices relative to import prices, and qt is
the real exchange rate. A non-zero Ψt implies imperfect
exchange rate pass-through to import prices. The backward-looking component,
yt-1, in the IS equation is motivated by the
assumption of habit persistence in consumer preferences.
is the foreign output
gap; and zt represents technology disturbances that follow
an AR(1)
process.[5]
Ψt = (1 — γ)st
— qt can be interpreted as the law of one price gap
which measures the deviation of the domestic price of imported goods from the world
price, where st is the terms of trade, defined
as export prices relative to import prices, and qt is
the real exchange rate. A non-zero Ψt implies imperfect
exchange rate pass-through to import prices. The backward-looking component,
yt-1, in the IS equation is motivated by the
assumption of habit persistence in consumer preferences.
The open economy new Keynesian Phillips curve derived by solving the firm's pricing decision can be written as:
where επ,t represents a cost-push shock. The Phillips curve is based on the assumption of monopolistically competitive firms, subject to pricing constraints (Calvo pricing and indexation). If g3 = 0, Equation (3) collapses down to a familiar closed-economy Phillips curve where inflation dynamics are partly driven by past and expected inflation in addition to the output gap. The open economy dimension includes the effects from the exchange rate as an important part of the monetary policy transmission process.
The assumption of perfect capital markets yields the standard uncovered interest parity condition (which links the expected exchange rate depreciation to the interest rate differential):
where Uq,t is a time-varying risk premium that follows an AR(1) process.
The monetary authority is assumed to set the nominal interest rate according to a Taylor rule based on contemporaneous inflation and output as well as an interest rate smoothing term:
where εr,t represents a non-systematic deviation from
the reaction function. To complete the description of the structural model,
the terms of trade st, the foreign output gap 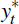 , foreign interest
rates
, foreign interest
rates
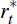 and foreign inflation
and foreign inflation 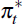 are assumed to follow exogenous AR(1) processes.
are assumed to follow exogenous AR(1) processes.
The structural model can be summarised as:
where 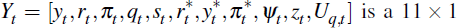 vector containing the state variables of model and
vector containing the state variables of model and 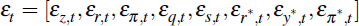 is an 8 × 1
vector of structural
innovations.[6]
The solution of the model can be represented as a first-order VAR:
is an 8 × 1
vector of structural
innovations.[6]
The solution of the model can be represented as a first-order VAR:
3.1 Data Description
Data from 1980:Q1 to 2006:Q1 for the Australian economy are used to estimate the
structural model and the
SVAR.[7]
The starting period coincides with previous SVAR studies of the Australian economy
including Dungey and Pagan (2000). Quarterly observations on real total GDP
(yt), headline CPI inflation (excluding interest
rates and taxes) (πt), the (goods and services) terms
of trade (st), the real exchange rate (qt),
the nominal interest rate (measured by the 90-day bank bill rate) (rt),
US GDP (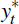 ),
US CPI inflation quarter-on-quarter (
),
US CPI inflation quarter-on-quarter (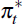 ) and US nominal interest
rate
(
) and US nominal interest
rate
(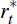 )
are sourced from the Reserve Bank of Australia, the Australian Bureau of Statistics
and the IMF's
International Financial Statistics (IFS)
database.[8]
)
are sourced from the Reserve Bank of Australia, the Australian Bureau of Statistics
and the IMF's
International Financial Statistics (IFS)
database.[8]
The cyclical component of GDP for both Australia and the United States – that is, the output gap measures – are constructed using the BN decomposition described earlier. Due to the unusual upswing in Australia's terms of trade between 2004 and 2006, this time series is detrended using an HP filter to ensure stationarity of the series. All variables apart from inflation and interest rates are entered in log form.
3.2 Estimating the DSGE Model
The parameters of the DSGE model are estimated using constrained maximum likelihood (ML). The likelihood function is computed via the state-space representation of the model's solution in Equation (7), together with the measurement equation linking the observed data and the state vector:
where: Zt denotes the observed data; and the matrix G specifies the relationship between the state variables and the observed data. The posterior parameter distribution is simulated using the Metropolis Hasting algorithm described in Lubik and Schorfheide (2007).
The ML estimates are generated conditional on the OLS estimate of the model's
four exogenous processes that explain developments in the rest of the world:
the terms of trade st, foreign inflation 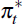 , foreign interest
rates
, foreign interest
rates
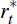 and foreign output gap
and foreign output gap 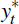 . There are two advantages in estimating
the observed exogenous processes independently of the model. First, it reduces
the number of parameters to be estimated in the simulation algorithm. Second,
Fukac and Pagan (2006) argue that rigid restrictions imposed by DSGE models
on the data may yield invalid estimates of the model's observable shocks
(that is, shocks that are mapped into actual data, such as the foreign output
gap
. There are two advantages in estimating
the observed exogenous processes independently of the model. First, it reduces
the number of parameters to be estimated in the simulation algorithm. Second,
Fukac and Pagan (2006) argue that rigid restrictions imposed by DSGE models
on the data may yield invalid estimates of the model's observable shocks
(that is, shocks that are mapped into actual data, such as the foreign output
gap 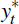 ).
).
The ML estimate of the model's parameters from the 1.5 million Markov chain draws are summarised in Table 1.[9] The set of Markov chain diagnostic tests imply that the simulated chains attain their stationary distributions.[10] The degree of backward-lookingness is estimated to be 0.09 for the IS equation (n1) and 0.27 for the Phillips curve (g1). The estimated coefficient on the real interest rate (n2) in the IS equation is relatively small, suggesting output variation is relatively insensitive to interest rate changes. The response of inflation to output gap changes (g2) is also estimated to be low. The Taylor rule displays a significant degree of interest rate smoothing behaviour with ρr estimated to be 0.90. The estimated weight on output is slightly higher than the weight on inflation and consistent with standard calibrated values used in the literature. However, as the estimation covers a period before the inflation-targeting regime, it is no surprise that there is a wide confidence interval around the Taylor-rule coefficient on output, ϕ2.
| Parameter | MLE statistics | Diagnostics | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | 2.5% | 97.5% | NSE(b) | p-value(c) | B-G(d) | ||
| IS equation | ||||||||
| n1 | 0.09 | 0.06 | 0.01 | 0.24 | 0.00 | 0.06 | 1.03 | |
| n2 | 0.01 | 0.01 | 0.00 | 0.04 | 0.00 | 0.75 | 1.00 | |
| n3 | 0.21 | 0.10 | 0.05 | 0.43 | 0.01 | 0.54 | 1.01 | |
| n4 | 0.26 | 0.09 | 0.15 | 0.50 | 0.01 | 0.02 | 1.12 | |
| n5 | −0.70 | 0.16 | −1.11 | −0.43 | 0.02 | 0.56 | 1.01 | |
| Phillips curve | ||||||||
| g1 | 0.27 | 0.05 | 0.16 | 0.37 | 0.01 | 0.93 | 1.00 | |
| g2 | 0.01 | 0.01 | 0.00 | 0.04 | 0.00 | 0.09 | 1.01 | |
| g3 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.24 | 1.00 | |
| Taylor rule | ||||||||
| ρr | 0.90 | 0.02 | 0.84 | 0.93 | 0.00 | 0.07 | 1.11 | |
| ϕ1 | 1.31 | 0.22 | 1.02 | 1.87 | 0.03 | 0.24 | 1.05 | |
| ϕ2 | 1.56 | 0.38 | 0.78 | 2.30 | 0.05 | 0.16 | 1.09 | |
| Persistence of shocks | ||||||||
| ρz | 0.78 | 0.07 | 0.62 | 0.89 | 0.01 | 0.22 | 1.04 | |
| ρu | 0.98 | 0.01 | 0.95 | 1.00 | 0.00 | 0.94 | 1.00 | |
| Std of shocks | ||||||||
| σz | 2.10 | 0.16 | 1.83 | 2.52 | 0.02 | 0.95 | 1.00 | |
| σπ | 1.03 | 0.22 | 0.72 | 1.54 | 0.03 | 0.36 | 1.03 | |
| σr | 1.10 | 0.08 | 0.97 | 1.28 | 0.01 | 0.92 | 1.00 | |
| σq | 1.78 | 0.13 | 1.55 | 2.06 | 0.02 | 0.13 | 1.05 | |
| Persistence of world shocks | ||||||||
| ρs | OLS | 0.90 | ||||||
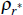 |
OLS | 0.94 | ||||||
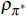 |
OLS | 0.62 | ||||||
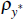 |
OLS | 0.29 | ||||||
| Std of world shocks | ||||||||
| σs | OLS | 1.75 | ||||||
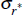 |
OLS | 1.07 | ||||||
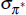 |
OLS | 1.67 | ||||||
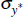 |
OLS | 4.14 | ||||||
| Notes: (a) The posterior statistics are computed based on 1 million draws
using the Markov Chains Monte Carlo method with a
50 per cent burn-in period. (b) Refers to the numerical standard error of the Markov chain. (c) Relates to the test of two means between the first and second half of the stationary Markov chain. (d) Refers to the Brooks and Gelman (1998) univariate distribution. |
||||||||
3.3 Qualitative Analysis of the DSGE Model's Impulse Response Functions
This section presents the impulse response functions of the model. The IRFs are simulated by sampling the empirical distribution of the estimates of the DSGE model. This takes into account the uncertainty of the responses associated with parameter uncertainty. The median along with the 5th and 95th percentile responses are shown in Figures B1 and B2. The IRFs of the model are broadly consistent with other open economy studies based on new Keynesian models. Moreover, the initial responses of key variables are generally quantitatively significant, providing a useful set of robust sign restrictions for the SVAR analysis. The discussion here will focus more on the initial responses rather than the dynamic adjustments to the shocks.
A positive technology shock decreases the output gap since actual output takes time to adjust in response to higher capacity. This causes the interest rate to fall. The real exchange rate depreciates to reflect the change in the interest rate differential, which contributes to a small increase in the inflation rate, despite the boost to productivity.
A cost-push shock increases inflation and leads to an increase in interest rates that causes the exchange rate to appreciate and output to contract.
A negative shock to the risk premium causes lower inflation and output due to an appreciating exchange rate. The monetary authority responds by reducing the interest rate. An unexpected tightening of monetary policy has a negative effect on the output gap, lowers inflation and appreciates the exchange rate.
Turning to external factors, following a positive shock to Australia's terms of trade, the output gap increases, the real exchange rate appreciates, and inflation and interest rates rise. An exogenous increase in the foreign interest rate leads to a depreciation of the domestic currency, which is sufficient to raise the output gap, and together these forces push up inflation. Given the simple structure of the model, an increase in foreign inflation has a similar but opposite effect on the domestic economy as an increase in the foreign nominal interest rate. An increase in foreign output actually decreases the domestic output gap, while both domestic inflation and interest rates stay relatively static and the depreciating exchange rate helps balance the international consumption risk-sharing condition.[11]
3.4 Robust Sign Restrictions
The focus of the study is to gather a set of sign restrictions from the impulse responses of the DSGE model to identify the small open economy SVAR. The complete set of estimated IRFs from the DSGE model provides more sign restrictions than are necessary to disentangle the eight structural shocks. The set of sign restrictions adopted is presented in Table 2.
| Shock | r* | y* | π* | y | r | π | q | s |
|---|---|---|---|---|---|---|---|---|
| Foreign interest rate | ↑ | – | ↓ | – | – | – | – | – |
| Foreign output | ↑ | ↑ | – | – | – | – | – | – |
| Foreign inflation | ↑ | ↓ | ↑ | – | – | – | – | – |
| Output (composite) | 0 | 0 | 0 | ↑ | ↑ | – | – | ↓ |
| Interest rate | 0 | 0 | 0 | – | ↑ | ↓ | – | – |
| Cost-push | 0 | 0 | 0 | ↓ | ↑ | ↑ | ↑ | – |
| Risk premium | 0 | 0 | 0 | – | – | ↓ | ↑ | – |
| Terms of trade | 0 | 0 | 0 | – | ↑ | ↑ | ↑ | ↑ |
| Notes: ↑ (↓) means positive (negative) response of the variables in columns to shocks in rows. 0 means no response (as implied by the small open economy assumption). – means no restriction is imposed on the response. | ||||||||
There are a few important things worth highlighting. First, given that the three foreign variables enter the structural model as exogenous driving processes, the set of sign restrictions imposed on the foreign economy follows the dynamic responses implied by a canonical closed-economy new Keynesian model. The responses of the domestic variables to the three foreign shocks are left unrestricted. Second, the terms of trade is treated as an endogenous variable and its response to other shocks, apart from the output shock, in the system is also left unrestricted.
With the presence of sticky home prices in the short run, the terms of trade responds to other variables in the system via changes to domestic inflation. Third, the output shock can be viewed as anything that moves output and interest rates together but is orthogonal to all other shocks in the system. Last, the sign restrictions are imposed for the initial two quarters only.
Footnotes
A positive innovation to technology will increase the potential output of the economy, hence has a negative effect on the output gap. [5]
In the numerical simulation and estimation of the model, the structural equation is solved using a solution algorithm described in Uhlig (1995). [6]
The effective sample period is from 1980:Q4 to 2006:Q1 after differencing and construction of the cyclical component of GDP. [7]
Data for the equivalent G7 series are also taken from the IFS and combined using the following weights: the United States (0.49); Japan (0.16); Germany (0.10); the United Kingdom (0.07); France (0.07); Italy (0.07); and Canada (0.04). [8]
A 50 per cent burn-in is discarded before computing the summary statistics. [9]
There is only one exception, n4, which is significant at the 5 per cent level. However, a small Brooks and Gelman statistic of 1.12 indicates that the chain has converged. [10]
Galí and Monacelli (2005) provide a detailed account of the way in which such a shock can lower domestic potential output. [11]