RDP 2008-08: The Role of International Shocks in Australia's Business Cycle Appendix A: Sign Restriction Algorithm

Define an (n × n) orthonormal rotation matrix Q such that:

where 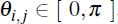. This provides a way of systematically exploring the space of all VMA representations by searching over the range of values of θ_i,j. While Canova and De Nicolo (2002) propose setting up a grid over the range of values for θ_i,j, the following algorithm generates the Qs randomly from a uniform distribution:

1. Estimate the VAR in Equation (10) using OLS to obtain the reduced form variance covariance matrix V and compute .
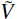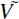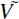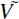2. Compute the Choleski decomposition of ₁₁ and ₂₂, where H₁₁ = chol(₁₁) and H₂₂ = chol(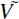₂₂).
3. For both the foreign and domestic block, draw a vector of θ_i,j from a uniform [0,π] distribution.
4. Calculate .
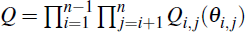5. Use the candidate rotation matrix Q to compute ε_t = HQe_t and its corresponding structural IRFs C(L) for domestic and foreign shocks.
6. Check whether the IRFs satisfy all the sign restrictions described in Table 2. If so keep the draw, if not, drop the draw.
7. Repeat (3)–(6) until 2,000 draws that satisfy the restrictions are found.