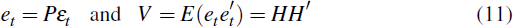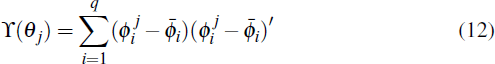RDP 2008-08: The Role of International Shocks in Australia's Business Cycle 4. Estimating a SVAR Model

This section sets out the small open economy sign-restricted VAR model estimated using the data described in Section 3.1. An eight-variable VAR(2) is fitted to quarterly observations from 1980:Q4 to 2006:Q1 where the number of lags are determined by the Akaike Information Criteria.

Consider a general VAR(p) model with n variables Y_t:

where: A(L) = A₁L + ... + A_p^Lp is a p^th order matrix polynomial; B is a (n × n) matrix of coefficients that reflect the contemporaneous relationships among Y_t; and ε_t is a set of (n × T) normally distributed structural disturbances with mean zero and variance covariance matrix 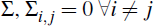. The structural representation in Equation (9) has the following reduced form:

where Π(L) = B⁻¹ A(L) and e_t is a set of (n × T) normally distributed reduced-form errors with mean zero and variance covariance matrix The aim is to map the statistical relationships summarised by the reduced-form errors e_t back into economic relationships described by ε_t. Let P = B⁻¹. The reduced-form errors are related to the structural disturbances in the following manner:

for some matrix H such that HH′ = PΣP′. An identification problem arises if there are not enough restrictions to uniquely pin down H from the matrix V.^[12]

4.1 Identification through Sign Restrictions

The identification of structural shocks is often a controversial issue, with different identifying assumptions leading to quite different conclusions. Typical restrictions employed in the literature are based on the short-run or long-run impact of certain shocks on a subset of variables. These are known as zero or constant restrictions. The Choleski decomposition is an example of one such strategy where the contemporaneous impact of shocks follows a recursive ordering. One noticeable feature of standard empirical DSGE models is that they almost never imply zero-type restrictions. This is also the case with the estimated structural model presented in Section 3.

The central idea behind SVAR analysis is to decompose the set of reduced-form shocks, characterised by V, into a set of orthogonal structural disturbances characterised by Σ. However, there are an infinite number of ways in which this orthogonality condition can be achieved. Let H be an orthogonal decomposition of V = HH′. The multiplicity arises from the fact that for any orthonormal matrix Q (where QQ′ = I), such that 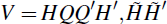is also an admissible decomposition of V, where 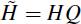. This decomposition does not have any economic content but nevertheless produces a set of uncorrelated shocks 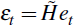, without imposing zero-type restrictions.

The identification strategy used here closely follows Canova and De Nicolo (2002), Peersman (2005) and Uhlig (2005) in using qualitative information directly from IRFs to achieve identification without the need to impose potentially invalid zero-type restrictions. Canova and De Nicolo proposed an algorithm to trace out all possible orthogonal VMA representations of the VAR consistent with a given set of sign restrictions. See Appendix A for a more detailed description of the algorithm.

4.2 Finding the Median Impulse

The next step is to construct a summary measure from all the VAR representations consistent with the given set of sign restrictions. A common approach is to examine all of the feasible IRFs implied, and report the median response at each horizon for each variable. However, Fry and Pagan (2005) criticise this approach since the implied ‘median’ IRF may not actually be a feasible response (since it is likely to consist of selected parts of paths implied by different candidate functions). In other words, inference is difficult because the orthogonality condition may be violated.

Fry and Pagan suggest locating a unique identification matrix such that all of the feasible impulses are closest to its median while maintaining the orthogonality condition. Each feasible VAR representation can be distinguished by the rotation angle, θ. So the objective is to choose θ so as to minimise:

where: the index i refers to the horizon for which the impulses are calculated; 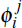is an n × n matrix of standardised impulses for the jth rotation; and 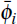is the median impulse over all possible rotations.^[13] Full details of the methodology and implementation are provided in Appendix A.

Footnotes

There are n² unknown elements in H with only n(n+1)/2 unique elements in V. [12]

In Fry and Pagan (2005), q is set to 1 focusing only on the initial period impulse. [13]