RDP 2008-08: The Role of International Shocks in Australia's Business Cycle 2. The Cyclical Component of GDP

The first step of the analysis in this paper is to obtain a measure of the cyclical component of GDP. The cyclical component is defined as the difference between the actual and the permanent component of GDP.^[1] The permanent component is extracted by means of a Beveridge-Nelson (BN) decomposition, which is preferred to one popular alternative, the Hodrick-Prescott (HP) filter, as the BN decomposition allows for correlation between the innovations to the permanent and cyclical components.

A time series y_t with an ARIMA(p,1,q) representation can be decomposed into a permanent (τ_t) and cyclical (c_t) component using the BN decomposition as follows:

where τ_t = µ + τ_t-1 + αε_t is the unobserved permanent component, which is assumed to follow a random walk with an average growth rate of µ; and c_t = ø_p(L)c_t + Ψ_q(L)ε_t + (1 − α)ε_t is a stationary and invertible ARMA(p,q) process, where ø_p(0) = 0 and Ψ_q(L) = 0.

Likelihood ratio tests suggest that an ARIMA(2,1,1) model provides the best empirical fit for Australian real GDP between 1980:Q4 and 2006:Q1.^[2] Figure 1 shows that the BN cycle is more volatile than the cycle derived using the HP filter (based on the smoothing parameter λ = 1,600). This is particularly so in the first half of the sample which displays more pronounced cycles.^[3] This may reflect the fact that the HP filter dampens long- and short-run growth cycles, while strongly amplifying growth cycles at the business cycle frequencies (5–7 years). As a result, the HP filter may induce spurious periodicity that does not necessarily exist in the underlying data. The two cycles have a similar frequency of peaks (estimated using the periodogram) of around 17 quarters over the sample, with the BN cycle containing noticeably more high-frequency oscillations.

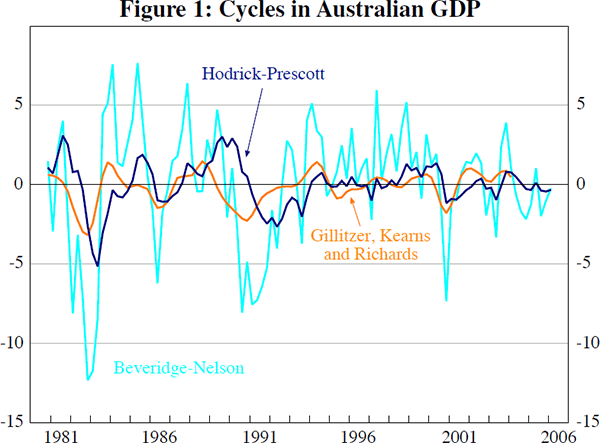
Figure 1 also shows the coincident (GKR) index of Australian economic activity derived by Gillitzer et al (2005) using a factor model. This index provides a plausible measure of the Australian business cycle using a large number of macroeconomic variables. For all three series, the two recessions during the early 1980s and 1990s are apparent. The BN cycle and GKR index coincide with respect to the timing of recessions, suggesting a bottoming out of economic activity around 1983:Q1 and 1991:Q1. The HP cycle is a bit slower at picking up the recessions.^[4] In addition, the BN cycle identifies two episodes of weak economic activity over the sample period. The first, in 1986, coincides with Paul Keating's banana republic remark over concerns about Australia's foreign debt position, a sharp depreciation of the exchange rate, and a downturn in household expenditure. The slowdown of the economy following the end of the Sydney Olympic Games and the introduction of the goods and services tax in 2000 is also apparent.

Footnotes

The terms permanent component and trend are used interchangeably, as are cyclical component and the cycle. A detailed review of various detrending methods can be found in Canova (1998). [1]

The BN decomposition is computed based on the method suggested by Newbold (1990). [2]

The standard deviation of the BN cycle is 3.9 per cent compared with 1.4 per cent for the HP cycle over the whole sample. [3]

The HP filter can be thought of as a two-step filter: in the first step it renders y_t stationary; in the second it smooths the resulting stationary series with asymmetric moving average (MA) weights, which can contribute to a delay in identifying the recessions. [4]