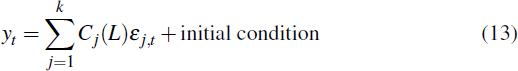RDP 2008-08: The Role of International Shocks in Australia's Business Cycle 5. Sign-restricted VAR Results
December 2008
- Download the Paper 373KB
The identification scheme based on the sign-restricted VAR allows for a structural interpretation of the effects of shocks. The impulse response of the output gap, the interest rate, inflation, the real exchange rate and the terms of trade with respect to the three foreign shocks are shown in Figure B3. An exogenous increase in the foreign interest rate results in a depreciation of the exchange rate which raises domestic inflation. In contrast to the DSGE model, the depreciation of the exchange rate is more gradual, reaching a peak at eight quarters before returning to equilibrium. A more important difference from the DSGE results is that output falls, which appears to reflect the decline in foreign output (not shown) and would also help to explain why domestic interest rates decline.
In contrast to the DSGE estimates, the sign-restricted VAR estimates imply that an increase in foreign output leads to a positive domestic output gap, reaching a peak after four quarters. The positive domestic output gap implies increased inflationary pressure, which induces a tightening of monetary policy over time to bring both output and inflation back to steady-state. The response of the domestic economy following a foreign inflation shock is very similar to that implied by the DSGE model. The exchange rate appreciates in response to the lower real interest rate differential. This leads to a fall in the output gap and subsequently a decline in inflation. There is a small monetary loosening to bring both output and inflation back to equilibrium.
Figures B3 and B4 display the summary IRFs from the sign-restricted VAR for the remaining five domestic shocks. A positive output shock (that is, a negative technology shock) raises the interest rate consistent with the sign restriction. This shock also induces inflationary pressure and the interest rate remains above its steady-state level for some time. An unanticipated tightening of monetary policy lowers both inflation and output while the exchange rate appreciates in response to higher real interest rates. After the shock, the interest rate falls so as to stimulate output and bring inflation back to its steady-state level. Following a positive cost-push shock, the domestic interest rate increases, the exchange rate appreciates and the output gap falls. A negative shock to the risk premium triggers an appreciation of the exchange rate leading to lower inflation. The monetary authority responds to this by lowering the domestic interest rate. In contrast to the structural model, the effect of the monetary response is estimated to outweigh the effect of the higher exchange rate, leading to higher output. A terms of trade shock has a positive effect on both output and inflation, leading to a tightening of monetary policy. The exchange rate also responds to the higher terms of trade, helping to stabilise both output and inflation.
5.1 Main Drivers of Output over the Business Cycle
Variance decompositions are often used to determine the relative contribution of shocks to the forecast error variance of a variable of interest over different horizons. As a benchmark, I first present a variance decomposition based on the Choleski decomposition. The variables are ordered according to the convention that the most exogenous (or predetermined) variables appear first. The variance decomposition results reported in Table 3 are based on the following ordering: foreign output, foreign inflation, the foreign interest rate, the terms of trade, the output gap, the interest rate, inflation and the real exchange rate. Investigation of other ordering schemes, where the order of output among the domestic variables varies from first to last, reveals little difference in the variance decomposition results for output. The benchmark results show that at the one-year horizon, shocks to the domestic output gap account for around two-thirds of the total variance in the output gap while other domestic factors play only a modest role. Foreign shocks account for just over one-quarter of the output gap forecast error variance, with the biggest contributor being foreign output accounting for around 16 per cent. At longer horizons, the role of domestic output shocks decreases slightly while other domestic factors play a slightly larger role. The contribution from all foreign factors stays fairly constant across the different forecasting horizons.
| Quarter | Shock | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Foreign interest rate | Foreign output gap | Foreign inflation |
Technology |
Interest rate |
Cost-push |
Risk premium |
Terms of trade |
||
| Output gap | |||||||||
| 1 | 0.3 | 2.0 | 7.5 | 89.0 | 0.0 | 0.0 | 0.0 | 1.2 | |
| 4 | 3.3 | 15.7 | 7.5 | 65.8 | 0.9 | 3.5 | 2.3 | 1.0 | |
| 8 | 3.1 | 14.8 | 8.9 | 62.1 | 1.9 | 4.5 | 3.3 | 1.4 | |
| 12 | 3.0 | 14.5 | 9.1 | 60.1 | 2.8 | 5.3 | 3.7 | 1.5 | |
| 50 | 3.0 | 14.4 | 9.1 | 58.6 | 3.8 | 5.8 | 3.8 | 1.6 | |
| Interest rate | |||||||||
| 1 | 0.7 | 0.1 | 1.2 | 3.7 | 90.5 | 1.6 | 0.0 | 2.1 | |
| 4 | 1.9 | 9.8 | 5.3 | 17.2 | 53.7 | 10.8 | 0.7 | 0.7 | |
| 8 | 5.1 | 16.7 | 4.5 | 24.9 | 35.7 | 12.3 | 0.3 | 0.4 | |
| 12 | 6.4 | 19.7 | 3.7 | 28.4 | 29.2 | 11.5 | 0.4 | 0.7 | |
| 50 | 8.9 | 23.0 | 2.9 | 29.1 | 22.5 | 9.1 | 1.1 | 3.4 | |
| Inflation | |||||||||
| 1 | 3.0 | 0.9 | 0.1 | 0.7 | 0.0 | 94.9 | 0.0 | 0.4 | |
| 4 | 2.7 | 2.4 | 1.8 | 0.9 | 12.1 | 74.1 | 4.0 | 2.0 | |
| 8 | 3.7 | 5.8 | 2.2 | 4.4 | 12.5 | 64.3 | 4.2 | 3.0 | |
| 12 | 5.1 | 8.4 | 2.0 | 6.8 | 11.6 | 58.2 | 4.5 | 3.4 | |
| 50 | 7.4 | 11.7 | 1.8 | 8.8 | 10.3 | 50.8 | 4.6 | 4.6 | |
| Real exchange rate | |||||||||
| 1 | 0.7 | 0.1 | 0.0 | 0.1 | 3.0 | 0.0 | 87.8 | 8.2 | |
| 4 | 0.7 | 0.1 | 6.8 | 3.2 | 2.8 | 3.9 | 80.5 | 2.1 | |
| 8 | 4.5 | 1.2 | 14.3 | 2.2 | 2.8 | 5.3 | 68.0 | 1.7 | |
| 12 | 9.3 | 2.8 | 17.6 | 1.7 | 6.5 | 5.3 | 55.1 | 1.7 | |
| 50 | 11.7 | 4.0 | 17.0 | 1.8 | 13.5 | 5.4 | 44.6 | 2.0 | |
Looking at the variance decomposition of the shocks identified by the sign-restricted VAR model reveals some important differences (Table 4). These results suggest that domestic output shocks only account for 4–5 per cent of the variation across all horizons. At the shorter horizons, all three foreign factors combine to account for more than 60 per cent of the output gap forecast error variance. A sizeable share of this appears to be due to foreign monetary policy innovations, although this may, in part, reflect factors that are outside of the model, such as global confidence, that are transmitted to the domestic economy via international financial markets. This view is consistent with the findings in Dungey and Pagan (2000), which show that international financial linkages are important when modelling the Australian economy. At the longer forecasting horizon, all three foreign factors maintain their influence on domestic output gap variations, with both the foreign interest rate and foreign output remaining the dominant contributors. Although the model treats the terms of trade as endogenous, realistically it can be thought of as exogenous, at least over longer horizons. So in this respect the terms of trade could be thought of as another foreign factor. The terms of trade account for a quarter of the variation in output across all but the shortest of horizons. This is consistent with the significance of commodities in Australian exports. Turning to domestic factors, interest rate shocks are estimated to have only a small influence on output gap fluctuations, while inflation (cost-push) and exchange rate (risk premium) shocks each contribute around 5–8 per cent to the variance of the output gap. This is broadly similar to the Choleski baseline results.
| Quarter | Shock | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Foreign interest rate | Foreign output gap | Foreign inflation |
Technology |
Interest rate |
Cost-push |
Risk premium |
Terms of trade |
||
| Output gap | |||||||||
| 1 | 49.1 | 0.0 | 1.5 | 5.2 | 0.2 | 0.7 | 7.4 | 35.9 | |
| 4 | 41.7 | 17.1 | 1.8 | 4.4 | 0.5 | 5.2 | 4.8 | 24.5 | |
| 8 | 40.5 | 17.0 | 1.9 | 4.4 | 0.5 | 6.6 | 4.8 | 24.3 | |
| 12 | 40.1 | 16.7 | 1.9 | 4.3 | 0.5 | 7.2 | 4.8 | 24.6 | |
| 50 | 39.4 | 16.6 | 2.0 | 4.4 | 0.5 | 7.5 | 5.0 | 24.6 | |
| Interest rate | |||||||||
| 1 | 2.4 | 2.2 | 5.6 | 11.1 | 3.1 | 6.6 | 59.4 | 9.5 | |
| 4 | 1.8 | 3.7 | 3.6 | 8.1 | 1.4 | 13.7 | 46.4 | 21.2 | |
| 8 | 1.6 | 20.3 | 1.9 | 7.3 | 1.4 | 10.3 | 34.4 | 22.6 | |
| 12 | 1.3 | 32.5 | 1.5 | 7.2 | 1.4 | 8.0 | 28.9 | 19.2 | |
| 50 | 1.1 | 54.7 | 1.6 | 5.2 | 1.0 | 5.5 | 18.6 | 12.3 | |
| Inflation | |||||||||
| 1 | 25.7 | 0.8 | 1.2 | 0.1 | 8.2 | 63.1 | 0.5 | 0.4 | |
| 4 | 19.6 | 3.1 | 1.6 | 3.7 | 6.0 | 44.2 | 19.8 | 2.1 | |
| 8 | 16.2 | 11.9 | 1.7 | 6.1 | 4.9 | 37.2 | 19.2 | 2.8 | |
| 12 | 14.1 | 21.4 | 1.5 | 6.5 | 4.3 | 32.3 | 17.5 | 2.5 | |
| 50 | 10.8 | 38.9 | 1.8 | 5.1 | 3.3 | 24.6 | 13.2 | 2.3 | |
| Exchange rate | |||||||||
| 1 | 0.5 | 2.2 | 23.3 | 43.9 | 2.7 | 1.0 | 26.2 | 0.1 | |
| 4 | 8.6 | 3.2 | 18.9 | 27.6 | 3.2 | 6.1 | 30.2 | 2.3 | |
| 8 | 13.2 | 11.9 | 12.7 | 20.2 | 4.0 | 12.6 | 21.1 | 4.4 | |
| 12 | 13.5 | 25.8 | 8.8 | 13.8 | 3.5 | 14.0 | 14.3 | 6.3 | |
| 50 | 10.7 | 40.0 | 7.8 | 9.4 | 2.5 | 11.9 | 10.1 | 7.5 | |
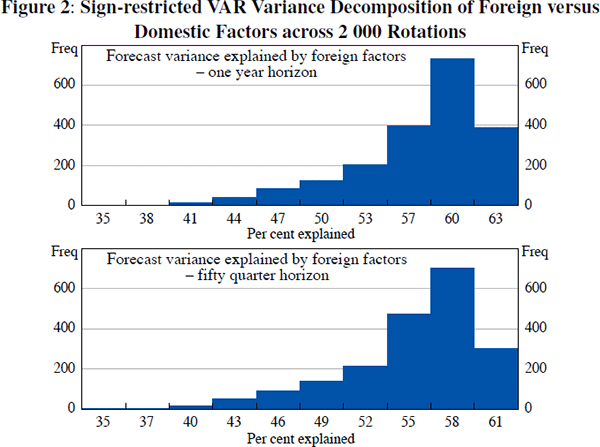
One may ask what is the role of foreign factors among other admissible rotations since it is impossible to distinguish them statistically. To check the sensitivity of the variance decomposition results around the optimised median impulse, the chosen median rotation is dropped and the next median impulse is found by re-optimising Equation (12) over the remaining admissible rotations. This procedure is repeated 50 times around the ‘median region’. The results imply that foreign factors explain between 45 to 60 per cent of the unconditional variance in output, with foreign interest rates remaining the dominant contributor. To give a more complete picture, Figure 2 plots the forecast error variance for the output gap attributed to foreign factors at both the one-year and 50-quarter horizon across all 2,000 admitted rotations.[14] The first point to note is that the results presented above lie exactly on the mode of the distribution, while the baseline Choleski decomposition lies in the thin tail of the distribution. Looking at the range of values from the sign-restricted VAR analysis, it appears that the true importance of foreign factors may not be easily captured by traditional Choleski decompositions that impose contemporaneous (zero) coefficient constraints.[15]
Variance decompositions may reveal which shocks are important at explaining the forecast errors of output across different horizons. However, Fry and Pagan (2005) argue they may not be very useful in understanding the nature of business cycle fluctuations. One useful statistic is to decompose the historical observation of output into its MA representation in terms of shocks, that is:
where Cj(L) is the impulse response to the shock j.[16] Historical decompositions are particularly useful in relating certain events that have happened over the business cycle.
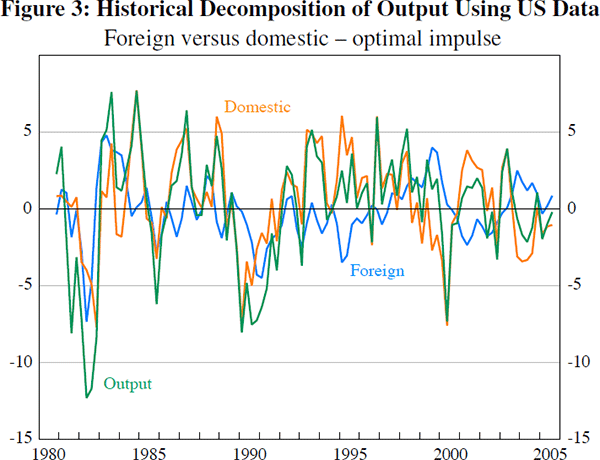
Figure 3 plots the historical decomposition of output into foreign (output, inflation and interest rates) versus domestic factors. During the two recessionary periods (the early 1980s and 1990s), both foreign and domestic factors had contributed negatively to output. This observation is consistent with the results reported in Dungey (2002). From the early 1990s onwards, the Australian economy experienced relatively stable and low inflation combined with robust output growth. Coincidentally, foreign and domestic shocks appear to have had offsetting effects so as to moderate domestic business cycle fluctuations during this period. For example, the slowdown in the economy after the Sydney Olympic Games together with the introduction of GST in 2,000 was somewhat offset by buoyant conditions before the bursting of the ‘dot-com’ bubble in the United States. A buoyant housing market and strong household consumption in the early part of this decade was moderated by a temporary downturn in the US economy following the terrorist attacks in September 2001. The pattern continued in late 2003 where slowing conditions in the Australian housing market were offset somewhat by a relatively strong US economy.
5.2 G7 as the Foreign Economy
To check the robustness of these results, the sign-restricted VAR model is re-estimated using G7 data as the foreign economy. The overall conclusion is supported, although minor differences do arise.[17]
The combined contribution of foreign shocks accounts for around 63 per cent of the forecast error variance for the output gap at the one-year horizon, similar to that reported earlier. At the 50-quarter horizon, this increases to 76 per cent in contrast to 59 per cent based on using only US data. Consistent with the earlier estimates, innovations from domestic output play a smaller role in explaining domestic output gap forecast errors. However, within the set of international variables, foreign output now takes on a larger role compared with foreign interest rates. This tends to suggest that interest rates may have been picking up other global factors in the results based on US output alone.
Footnotes
The contribution from domestic factors can be easily read off the figure since the two factors must sum to 100. [14]
Estimating the sign-restricted VAR over the shorter sample 1992:Q1– 2006:Q1 suggests that, if anything, foreign output shocks have become more important for explaining the variance of the domestic output gap, while shocks to foreign interest rates have become less so. However, this sample may be too short to produce reliable estimates of the relatively high-dimensional VAR. [15]
Since the entire history of shocks is not observed, the decomposed components of yt may not add up exactly for the initial periods of the sample. In the case of output, this is around six to eight quarters, which are dropped from the decomposition results shown in Figure 3 below. [16]
Detailed statistics are not reported but are available upon request. [17]