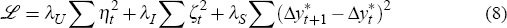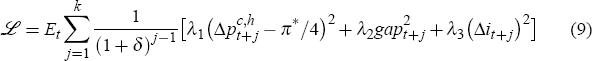RDP 2005-11: A Small Model of the Australian Macroeconomy: An Update 3. Remaining Components of the Model
December 2005
- Download the Paper 628KB
In this section we summarise the remaining key aspects of the model. These are: the model's estimation of potential output and the output gap over history; the steady-state assumptions adopted for the model's exogenous variables to ensure that it displays appropriate long-run behaviour under any suitably stabilising monetary policy reaction function; and finally, an outline of one such reaction function, namely optimal policy with respect to a standard quadratic loss function.
3.1 Potential Output
The non-farm output gap is defined as the difference between actual and potential non-farm output, as a percentage of potential output. This gap plays a central role in the model, appearing as an explanatory variable in both the model's inflation and unit labour cost equations. It is designed to capture inflationary pressures, with a zero gap consistent with constant ongoing inflation in steady state (assuming bond market inflation expectations are equal to this constant inflation rate).
We obtain estimates of the output gap for Australia directly within the model. In this section we briefly describe how this is done and discuss the results of the estimation process. Further details are provided in Appendix A.
There are various ways to estimate potential output, a number of which were reviewed by de Brouwer (1998) for Australia. In Beechey et al (2000) potential output was calculated by iteratively applying a Hodrick–Prescott filter to non-farm output, and adjusting the level of this filtered series so as to ensure the model's unit labour cost equation satisfied a vertical long-run Phillips curve constraint (see pp 29–33 of Beechey et al for further details). While not dissimilar, we now use instead a multivariate filter, like that used by Gruen, Robinson and Stone (2002). This filter estimates potential output using information from the model about the relationships between the output gap, consumer prices and unit labour costs.
Since the output gap reflects short-term inflationary pressures in consumer prices
and unit labour costs, one would expect it to be positive when the inflation
rates of these variables are rising, and negative when they are
falling (all other influences equal). The multivariate filter exploits
these relationships by iteratively searching for the potential output series
(and, hence, output gap) which provides the best fit to the model's unit
labour cost and underlying inflation equations, subject to a smoothness
criterion.[31] Formally,
it seeks the potential output series 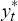 which minimises the
loss function
which minimises the
loss function
where ηt and ζt are the residuals from the unit labour cost and underlying inflation equations. The third term penalises volatility in the growth rate of potential output, encouraging the algorithm to allow only gradual changes in this growth rate over time. The weights λU, λI and λS determine the relative weight given to each of the three terms. Further details on the solution for potential output and the role of the weights are given in Appendix A.
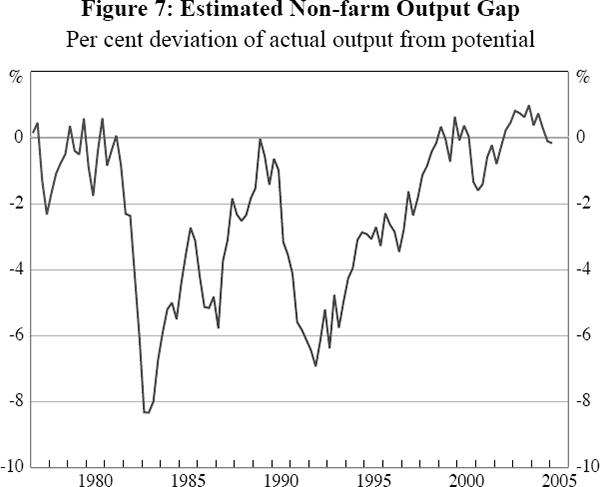
The resultant estimates of the output gap are shown in Figure 7. The gap displays a prominent cyclical pattern, with the recessions of 1982–83 and 1990–91 marked by sharp falls. Following both recessions are periods of above-potential growth, when the output gap narrowed. Most recently, the gap has remained around zero. However, it has been below zero on average over the sample period. As noted in Gruen et al (2002, p 12), this is consistent with the decline in the inflation rate over the 1980s and 1990s, especially given that bond market inflation expectations were almost invariably above actual inflation over this period.[32]
3.2 Steady State Assumptions
Table 7 summarises our assumptions with regard to the steady-state behaviour of the model's exogenous variables. With these assumptions, we can deduce the steady-state properties of the model's six endogenous variables. By this we mean the levels or growth rates to which these variables would converge in the long run, in the absence of future shocks (and with monetary policy set in a suitably stabilising fashion).[33] These steady-state properties are set out in Table 8.
| Variable | Steady state assumption |
|---|---|
| Δy* | The steady state growth rate of potential non-farm output is assumed to equal 3.25 per cent per annum. |
| tot | In steady state the goods terms of trade is assumed to equal its average value over the sample 1985:Q1 to 2005:Q1. |
| s | The real share accumulation index is assumed to be at trend in steady state, so that the de-trended series is zero. |
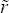 |
The neutral real cash rate is assumed to be 3.0 per cent per annum. A necessary but not sufficient condition for the model to converge to steady state in the long run, in the absence of ongoing exogenous shocks, is that monetary policy be set such that the real cash rate converges to this neutral level. |
| Δpcom | In steady state, Australian commodity prices are assumed not to be changing in foreign currency terms. |
| πe,bm | In steady state, bond market inflation expectations are assumed to equal the target rate for headline inflation set by policy-makers (assumed to be 2.5 per cent per annum, the midpoint of the RBA's medium-term target for inflation). |
| soi | The Southern Oscillation Index is assumed to equal zero (corresponding to average rainfall) in steady state. |
| trf | The average tariff rate on imports is assumed to remain constant in steady state. |
| gapUS | The US output gap is assumed to close to zero in steady state. |
| rf | In steady state the world (G3) real interest rate is assumed to equal its average value (of 1.84 per cent) over the sample 1985:Q1 to 2005:Q1. |
| sUS | The US real share accumulation index is assumed to be at trend in steady state, so that the de-trended series is zero. |
| Δpc,f | Trade-weighted foreign consumer price inflation is assumed to equal 0.5 per cent per quarter, close to its average value over the sample 1985:Q1 to 2005:Q1. |
| Δpx,f | Trade-weighted foreign export price inflation is assumed to be zero in steady state (consistent with 2 per cent annual foreign consumer price inflation, offset by a Balassa-Samuelson adjustment of the same magnitude as for Australia). |
| Δpusoil | In steady state the US$ price of oil is assumed to rise at the same annual rate as trade-weighted foreign consumer prices (while the US$/A$ exchange rate, used to derive an A$ oil price, is assumed to move in line with changes in the trade-weighted exchange rate). |
| trendpm | The trend in the import price equation, after increasing linearly over history, is assumed to cease rising at some point, so remaining constant in steady state. |
| Note: The choice of 3.25 per cent for the steady state growth rate of potential output represents a round number a little below the average growth rate of Australian non-farm GDP over the past decade, during which the output gap is assessed to have been closing from an initially negative level. It is also consistent with the out-year GDP growth rate projection recently adopted by the Australian Treasury in the 2005–06 Budget. | |
| Variable | Steady state property |
|---|---|
| gap | The output gap closes to an equilibrium level of zero in steady state. Hence, the growth rate of non-farm output in steady-state is equal to that of potential output, which is assumed to be 3.25 per cent per annum. |
| rer | The real exchange rate is constant in steady state at a level determined by the (constant, exogenously set) long-run levels of: the goods terms of trade; and the real interest differential between Australia and the rest of the world (where real interest rates in both regions are assumed to revert to neutral). |
| Δpm | Import price inflation is constant in steady state at a rate equal to that of foreign export price inflation plus the differential between steady-state domestic and foreign consumer price inflation. This rate would thus be 0.5 per cent per annum in the event that the steady-state rate of domestic consumer price inflation were 2.5 per cent per annum. |
| Δulc* | (Smoothed) economy-wide unit labour cost inflation is constant in steady state at a rate equal to that of headline inflation. |
| Δpc,h | Headline consumer price inflation is constant in steady state at a rate determined by policy-makers. Under the optimal policy routine described in Section 3.3 below, this constant rate is assumed to be 2.5 per cent per annum, the midpoint of the RBA's medium term inflation target. |
| Δpc,u | Underlying consumer price inflation is constant in steady state at a rate equal to that of headline inflation. |
Beginning with the real side of the model, the core autoregressive structure of the output gap equation, with a coefficient on the first lag of the gap between zero and one, ensures that in steady state the output gap must equal zero. Hence, the steady-state growth rate of non-farm output in the model simply equals the exogenously imposed long-run growth rate of potential output – which is currently set at 3.25 per cent per annum.[34] The real exchange rate is constant in steady state, consistent with an assumption of no long-run differential between the productivity growth rates of Australia and her trading partners.
Turning to the nominal side of the model, as discussed in Beechey et al (2000) the homogeneity restrictions we impose upon the model's price equations have several implications for its behaviour in steady state. First, since the consumer price equations exhibit static homogeneity and PPP is imposed in the import price equation, no real variables are affected in the long run by sustained level shifts in either consumer prices or import prices.[35] Indeed, these restrictions are enough to ensure that long-run neutrality also holds with respect to sustained shifts in the level of unit labour costs, notwithstanding that the model's unit labour cost equation exhibits dynamic rather than static homogeneity.
Empirically, however, there remains a lack of dynamic homogeneity in both the model's consumer price and import price equations. For the consumer price equations this implies that, were there to be a shift in the steady-state rate of inflation, this would have a permanent effect on the mark-up of consumer prices over input costs (as well as the level of real unit labour costs). Likewise, for the import price equation the lack of dynamic homogeneity implies that, were the steady-state rate of import price growth to change, this would have a permanent effect on the margin between the cost of imported goods and their landed prices (as given by foreign export prices converted to Australian dollars). As noted in Beechey et al (2000), while it is difficult to see theoretically why such shifts would occur, there is some empirical evidence for such phenomena (see, for example, Banerjee and Russell 1999).
3.3 Optimal Policy
Short-term model-based forecasts often assume that the nominal interest rate is held constant over the forecast horizon, to assess how the economy might evolve were policy to remain unchanged. A common supplement to such an approach is to allow monetary policy to be determined by some suitable rule, such as a Taylor rule or an optimal policy routine.
Optimal policy routines determine the future path for a policy instrument – in the current setting, the cash rate – on the basis of a summary measure (loss function) which quantifies the objectives of policy, and the relative preference policy-makers attach to achieving each. While central banks would never, of course, actually implement policy simply to mechanically minimise such a loss function, such routines can provide a useful theoretical benchmark for ex post assessments of the stance of policy or for other research purposes.
Common objectives considered for optimal policy routines used to analyse monetary policy issues include: that year-ended inflation should be at some target level, π* (which for Australia we assume to be 2.5 per cent per annum, the midpoint of the Reserve Bank's medium-term target); that output should be at potential, so that the output gap is zero; and that movements in the cash rate, it, should be kept to a minimum, so as not to induce unnecessary volatility in financial markets. Optimal policy based on such objectives would typically be implemented by solving for the policy interest rate that minimises the expected value of the quadratic loss function
where: Et represents expectations at time t; k denotes the length of the horizon over which policy-makers assess their loss; δ represents a time discount factor; and λ1, λ2 and λ3 denote the respective weights attached by policy-makers to avoiding deviations of inflation from target, of the output gap from zero, and of this period's interest rate from last period's.[36] Minimising such a loss function provides one natural way of selecting a stabilising path for future interest rates under which the model's variables would be expected to converge over time towards their steady state levels or growth rates (absent unforeseen future shocks to the economy).[37]
Footnotes
Since underlying and headline inflation are generally quite similar, we condition our potential output estimates only on the former. Underlying inflation is less volatile and easier to model, which may make its equation better suited for use in estimating potential output. [31]
Bond market inflation expectations are, of course, difficult to measure – even for the period during which Australia has been issuing inflation indexed bonds (given the illiquidity of these instruments relative to nominal bonds). Nevertheless, our bond market expectations series fits well with what one might expect regarding the relativities between it and actual inflation over history. The former remained below the latter for several years following the initial step-up in inflation in the early to mid 1970s, as markets expected policy-makers to regain control over inflation. Thereafter, following the further spike in inflation in the late 1970s, bond market expectations stayed persistently above actual inflation until around five years after the sustained downward shift in Australian inflation in the early 1990s, when markets finally became convinced of policy-makers' determination to prevent any renewed outbreak of inflation. Figure 3 in Gruen, Robinson and Stone (2005) also suggests that, with regard to any errors introduced into the gap estimates shown in Figure 7 by problems with measuring bond market inflation expectations, these are likely to be small compared with those entailed by excluding a role for such expectations in the model's unit labour cost conditioning equation altogether. [32]
One method for setting monetary policy so that such convergence occurs is described in Section 3.3. [33]
By contrast, the core of Beechey et al's model of domestic output growth was a cointegrating relationship between Australian and US real output, so that steady-state domestic output growth was determined by an exogenous assumption about the potential growth rate of US output. [34]
To illustrate, suppose (for simplicity) that the model were in steady state, and that the level of underlying consumer prices then increased by (say) 1 per cent and remained this far above baseline thereafter (but with the steady state growth rates of all nominal variables unchanged). In the long run, this would induce a 1 per cent devaluation in the nominal exchange rate (noting that the long-run real exchange rate would be unaffected), which would raise the level of import prices by 1 per cent relative to baseline (in view of the PPP restriction in the model's import price equation). This would then force unit labour costs (both economy-wide and Balassa-Samuelson adjusted) to equilibrate to a level 1 per cent higher than baseline, as a result of the static homogeneity restriction in the model's underlying inflation equation; which would also then cause headline consumer prices to settle at a level 1 per cent above baseline. [35]
A common choice is to place equal weights on the output gap and deviations of inflation from target (λ1 = λ2), with λ3 then chosen so that the routine yields interest rate paths which display a degree of volatility, in the face of typical shocks, broadly consistent with that seen over history. [36]
A description of the main elements of the linear algebra involved in implementing such a routine in the current model is set out in Shuetrim and Thompson (1999) – albeit in the context of a stochastic simulations process. [37]